Question Number 141768 by loveineq last updated on 23/May/21
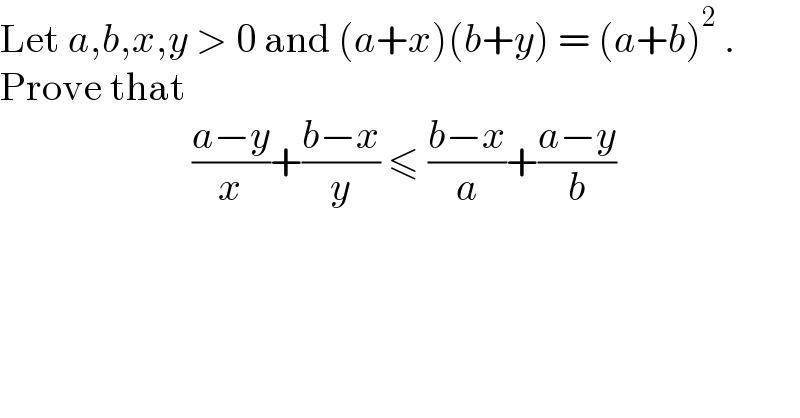
$$\mathrm{Let}\:{a},{b},{x},{y}\:>\:\mathrm{0}\:\mathrm{and}\:\left({a}+{x}\right)\left({b}+{y}\right)\:=\:\left({a}+{b}\right)^{\mathrm{2}} \:.\:\:\:\:\:\:\:\: \\ $$$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{a}−{y}}{{x}}+\frac{{b}−{x}}{{y}}\:\leqslant\:\frac{{b}−{x}}{{a}}+\frac{{a}−{y}}{{b}}\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$
