Let-E-be-a-banach-space-Y-is-normed-space-and-suppose-that-Ta-a-A-B-E-Y-If-Tax-a-A-Y-is-bounded-for-all-x-E-then-Ta-a-A-is-bounded-

Tinku Tara June 3, 2023 Probability and Statistics 0 Comments

Question Number 7499 by Tawakalitu. last updated on 31/Aug/16

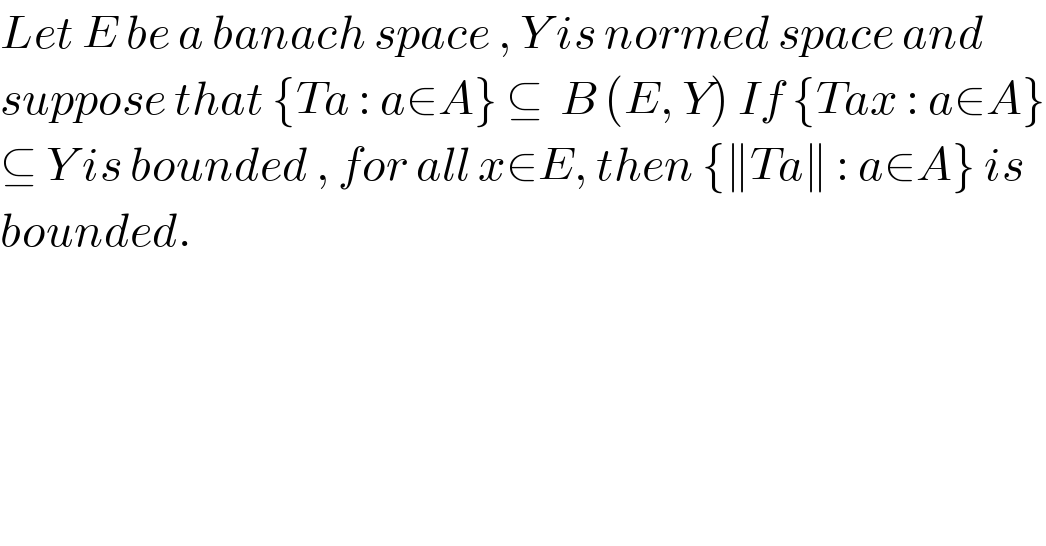
Let E be a banach space , Y is normed space and suppose that {Ta : a∈A} ⊆ B (E, Y) If {Tax : a∈A} ⊆ Y is bounded , for all x∈E, then {∥Ta∥ : a∈A} is bounded.

$${Let}\:{E}\:{be}\:{a}\:{banach}\:{space}\:,\:{Y}\:{is}\:{normed}\:{space}\:{and}\: \\ $$$${suppose}\:{that}\:\left\{{Ta}\::\:{a}\in{A}\right\}\:\subseteq\:\:{B}\:\left({E},\:{Y}\right)\:{If}\:\left\{{Tax}\::\:{a}\in{A}\right\} \\ $$$$\subseteq\:{Y}\:{is}\:{bounded}\:,\:{for}\:{all}\:{x}\in{E},\:{then}\:\left\{\parallel{Ta}\parallel\::\:{a}\in{A}\right\}\:{is}\: \\ $$$${bounded}. \\ $$

Facebook Tweet Pin

Let-E-be-a-banach-space-Y-is-normed-space-and-suppose-that-Ta-a-A-B-E-Y-If-Tax-a-A-Y-is-bounded-for-all-x-E-then-Ta-a-A-is-bounded-

Leave a Reply Cancel reply