Question Number 78269 by msup trace by abdo last updated on 15/Jan/20
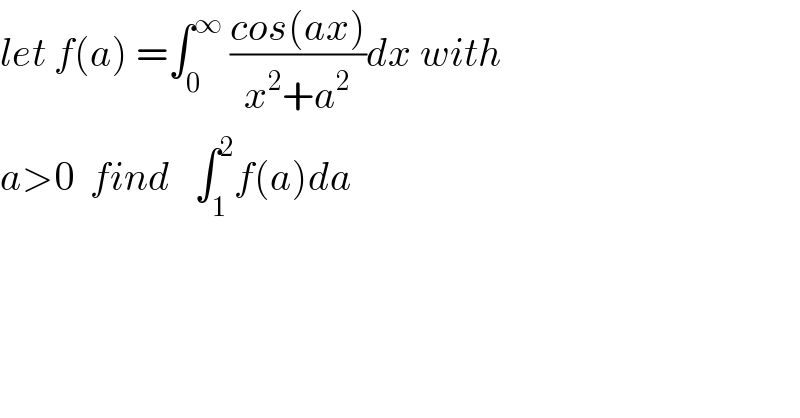
$${let}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{cos}\left({ax}\right)}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx}\:{with} \\ $$$${a}>\mathrm{0}\:\:{find}\:\:\:\int_{\mathrm{1}} ^{\mathrm{2}} {f}\left({a}\right){da} \\ $$
Commented by mathmax by abdo last updated on 15/Jan/20
![we have 2f(a) =∫_(−∞) ^(+∞) ((cos(ax))/(x^2 +a^2 ))dx =Re(∫_(−∞) ^(+∞) (e^(iax) /(x^2 +a^2 ))dx) let W(z)=(e^(iaz) /(z^2 +a^2 )) ⇒W(z)=(e^(iaz) /((z−ia)(z+ia))) so the poles of W are ia and −ia ⇒∫_(−∞) ^(+∞) W(z)dz =2iπ Res(W,ia) =2iπ×(e^(ia(ia)) /(2ia)) =(π/a) e^(−a^2 ) =2f(a) ⇒f(a) =(π/(2a))e^(−a^2 ) ⇒ ∫_1 ^2 f(a)da =(π/2)∫_1 ^2 (e^(−a^2 ) /a)da and a form of serie e^(−a^2 ) =Σ_(n=0) ^∞ (((−a^2 )^n )/(n!)) =Σ_(n=0) ^∞ (((−1)^n a^(2n) )/(n!)) ⇒ (e^(−a^2 ) /a) =Σ_(n=0) ^∞ (((−1)^n )/(n!)) a^(2n−1) ⇒∫_1 ^2 (e^(−a^2 ) /a)da =Σ_(n=0) ^∞ (((−1)^n )/(n!))[(1/(2n))a^(2n) ]_1 ^2 =Σ_(n=0) ^∞ (((−1)^n )/((2n)n!))( 2^(2n) −1) ⇒ ∫_1 ^2 f(a)da =(π/2)Σ_(n=0) ^∞ (((−1)^n )/((2n)n!))(4^n −1)](https://www.tinkutara.com/question/Q78308.png)
$${we}\:{have}\:\mathrm{2}{f}\left({a}\right)\:=\int_{−\infty} ^{+\infty} \:\frac{{cos}\left({ax}\right)}{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }{dx}\:={Re}\left(\int_{−\infty} ^{+\infty} \:\frac{{e}^{{iax}} }{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }{dx}\right) \\ $$$${let}\:{W}\left({z}\right)=\frac{{e}^{{iaz}} }{{z}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\:\Rightarrow{W}\left({z}\right)=\frac{{e}^{{iaz}} }{\left({z}−{ia}\right)\left({z}+{ia}\right)}\:\:{so}\:{the}\:{poles}\:{of}\:{W}\:{are} \\ $$$${ia}\:{and}\:−{ia}\:\:\Rightarrow\int_{−\infty} ^{+\infty} {W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left({W},{ia}\right) \\ $$$$=\mathrm{2}{i}\pi×\frac{{e}^{{ia}\left({ia}\right)} }{\mathrm{2}{ia}}\:=\frac{\pi}{{a}}\:{e}^{−{a}^{\mathrm{2}} } =\mathrm{2}{f}\left({a}\right)\:\Rightarrow{f}\left({a}\right)\:=\frac{\pi}{\mathrm{2}{a}}{e}^{−{a}^{\mathrm{2}} \:} \Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} {f}\left({a}\right){da}\:=\frac{\pi}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{{e}^{−{a}^{\mathrm{2}} } }{{a}}{da}\:\:{and}\:{a}\:{form}\:{of}\:{serie} \\ $$$${e}^{−{a}^{\mathrm{2}} } \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−{a}^{\mathrm{2}} \right)^{{n}} }{{n}!}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} \:{a}^{\mathrm{2}{n}} }{{n}!}\:\Rightarrow \\ $$$$\frac{{e}^{−{a}^{\mathrm{2}} } }{{a}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\:{a}^{\mathrm{2}{n}−\mathrm{1}} \:\Rightarrow\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{e}^{−{a}^{\mathrm{2}} } }{{a}}{da} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\left[\frac{\mathrm{1}}{\mathrm{2}{n}}{a}^{\mathrm{2}{n}} \right]_{\mathrm{1}} ^{\mathrm{2}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}\right){n}!}\left(\:\mathrm{2}^{\mathrm{2}{n}} −\mathrm{1}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} {f}\left({a}\right){da}\:=\frac{\pi}{\mathrm{2}}\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}\right){n}!}\left(\mathrm{4}^{{n}} −\mathrm{1}\right) \\ $$
Answered by mind is power last updated on 15/Jan/20
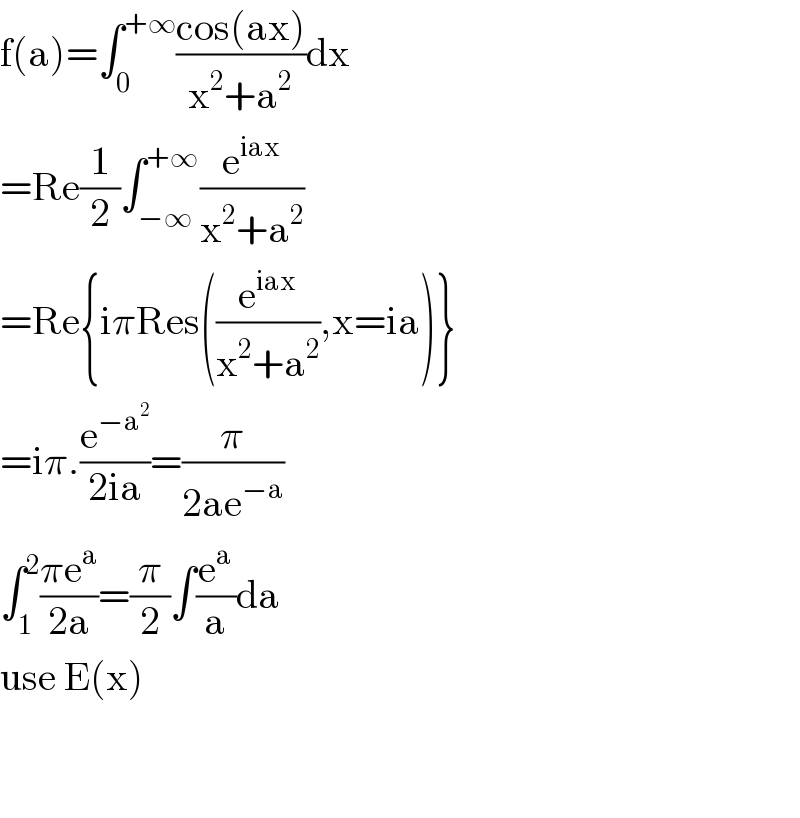
$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{cos}\left(\mathrm{ax}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\mathrm{Re}\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{\mathrm{e}^{\mathrm{iax}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} } \\ $$$$=\mathrm{Re}\left\{\mathrm{i}\pi\mathrm{Res}\left(\frac{\mathrm{e}^{\mathrm{iax}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} },\mathrm{x}=\mathrm{ia}\right)\right\} \\ $$$$=\mathrm{i}\pi.\frac{\mathrm{e}^{−\mathrm{a}^{\mathrm{2}} } }{\mathrm{2ia}}=\frac{\pi}{\mathrm{2ae}^{−\mathrm{a}} } \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\pi\mathrm{e}^{\mathrm{a}} }{\mathrm{2a}}=\frac{\pi}{\mathrm{2}}\int\frac{\mathrm{e}^{\mathrm{a}} }{\mathrm{a}}\mathrm{da} \\ $$$$\mathrm{use}\:\mathrm{E}\left(\mathrm{x}\right)\: \\ $$$$ \\ $$$$ \\ $$
