Question Number 66060 by mathmax by abdo last updated on 08/Aug/19
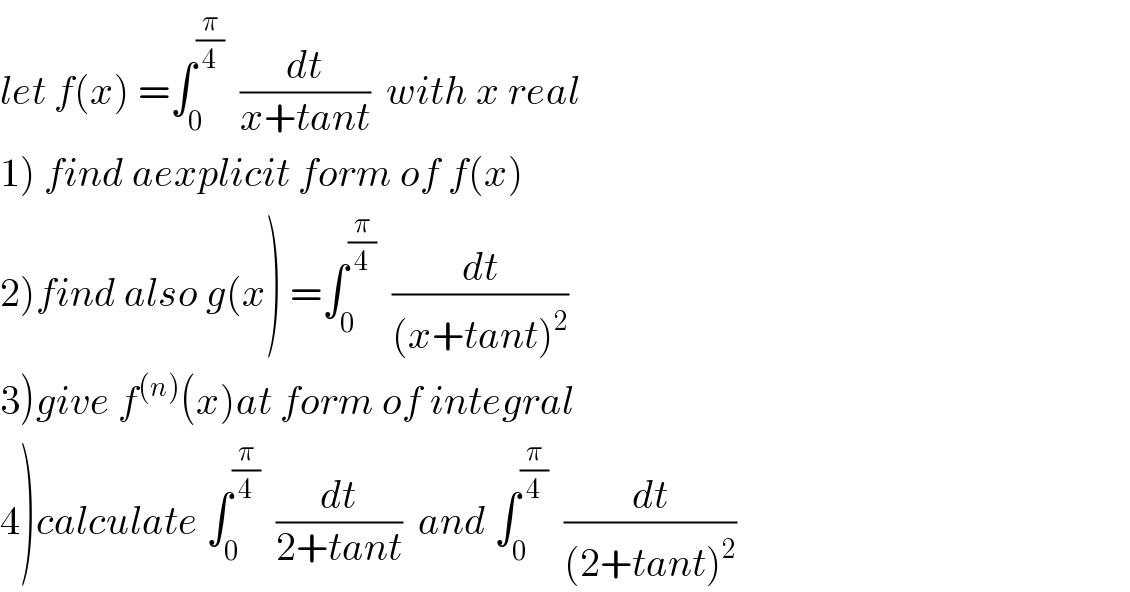
$${let}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dt}}{{x}+{tant}}\:\:{with}\:{x}\:{real} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{aexplicit}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right){find}\:{also}\:{g}\left({x}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dt}}{\left({x}+{tant}\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{3}\right){give}\:{f}^{\left({n}\right)} \left({x}\right){at}\:{form}\:{of}\:{integral} \\ $$$$\left.\mathrm{4}\right){calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dt}}{\mathrm{2}+{tant}}\:\:{and}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dt}}{\left(\mathrm{2}+{tant}\right)^{\mathrm{2}} } \\ $$
Commented by mathmax by abdo last updated on 10/Aug/19
![1) we have f(x)=∫_0 ^(π/4) (dt/(x+tant)) changement tan((t/2))=u give f(x)=∫_0 ^((√2)−1) (1/(x+((2u)/(1−u^2 )))) ((2du)/(1+u^2 )) =2∫_0 ^((√2)−1) ((1−u^2 )/((1+u^2 )(x−xu^2 +2u)))du =2 ∫_0 ^((√2)−1) ((u^2 −1)/((u^2 +1)(xu^2 −2u−x)))du let decompose F(u) =((u^2 −1)/((u^2 +1)(xu^2 −2u−x))) xu^2 −2u−x=0 →Δ^′ =1+x^2 ⇒u_1 =((1+(√(1+x^2 )))/x) and u_2 =((1−(√(1+x^2 )))/x) ( we suppose x≠0) ⇒F(u) =((u^2 −1)/(x(u−u_1 )(x−u_2 )(u^2 +1))) =(a/(u−u_1 )) +(b/(u−u_2 )) +((cu +d)/(u^2 +1)) a =lim_(u→u_1 ) (u−u_1 )F(u) =((u_1 ^2 −1)/(x(2((√(1+x^2 ))/x))(u_1 ^2 +1))) =((u_1 ^2 −1)/(2(√(1+x^2 ))(u_1 ^2 +1))) b =lim_(u→u_2 ) (u−u_2 )F(u) =((u_2 ^2 −1)/(x(−2((√(1+x^2 ))/x))(u_2 ^2 +1))) =((u_2 ^2 −1)/(−2(√(1+x^2 ))(u_2 ^2 +1))) lim_(u→+∞) uF(u) =0 =a+b +c ⇒c =−(a+b) F(0)=(1/x) =−(a/u_1 )−(b/u_2 ) +d ⇒d =(1/x)+(a/u_1 ) +(b/u_2 ) ⇒ ∫_0 ^((√2)−1) F(u)du =[aln∣u−u_1 ∣+bln∣u−u_2 ∣]_1 ^((√2)−1) +[(c/2)ln(u^2 +1)+darctan(u)]_0 ^((√2)−1) =aln∣(((√2)−1−u_1 )/(1−u_1 ))∣+bln∣(((√2)−1−u_2 )/(1−u_2 ))∣+(c/2)ln(3−2(√2)+1)+d arctan((√2)−1)} ⇒f(x)=2aln∣(((√2)−1−u_1 )/(1−u_1 ))∣+2bln∣(((√2)−1−u_2 )/(1−u_2 ))∣+cln(4−2(√2))+(dπ/4) a =(((((1+(√(1+x^2 )))/x))^2 −1)/(2(√(1+x^2 ))((((1+(√(1+x^2 )))/x))^2 +1))) =(((1+(√(1+x^2 )))^2 −x^2 )/(2(√(1+x^2 ))((1+(√(1+x^2 )))^2 +x^2 ))) =((1+2(√(1+x^2 ))+1+x^2 −x^2 )/(2(√(1+x^2 ))(1+2(√(1+x^2 ))+1+x^2 +x^2 ))) =(((1+(√(1+x^2 ))))/( (√(1+x^2 ))(2+2(√(1+x^2 ))+2x^2 ))) =((1+(√(1+x^2 )))/(2(√(1+x^2 ))(x^2 +2(√(1+x^2 ))+1))) rest to simplify other coefficie7ts...](https://www.tinkutara.com/question/Q66195.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{{dt}}{{x}+{tant}}\:\:{changement}\:{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}\:{give} \\ $$$${f}\left({x}\right)=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\:\frac{\mathrm{1}}{{x}+\frac{\mathrm{2}{u}}{\mathrm{1}−{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\mathrm{2}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left({x}−{xu}^{\mathrm{2}} \:+\mathrm{2}{u}\right)}{du} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{{u}^{\mathrm{2}} −\mathrm{1}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({xu}^{\mathrm{2}} −\mathrm{2}{u}−{x}\right)}{du}\:{let}\:{decompose} \\ $$$${F}\left({u}\right)\:=\frac{{u}^{\mathrm{2}} −\mathrm{1}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({xu}^{\mathrm{2}} −\mathrm{2}{u}−{x}\right)} \\ $$$${xu}^{\mathrm{2}} −\mathrm{2}{u}−{x}=\mathrm{0}\:\rightarrow\Delta^{'} \:=\mathrm{1}+{x}^{\mathrm{2}} \:\Rightarrow{u}_{\mathrm{1}} =\frac{\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}}\:\:{and}\:{u}_{\mathrm{2}} =\frac{\mathrm{1}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}} \\ $$$$\left(\:{we}\:{suppose}\:{x}\neq\mathrm{0}\right)\:\Rightarrow{F}\left({u}\right)\:=\frac{{u}^{\mathrm{2}} −\mathrm{1}}{{x}\left({u}−{u}_{\mathrm{1}} \right)\left({x}−{u}_{\mathrm{2}} \right)\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$=\frac{{a}}{{u}−{u}_{\mathrm{1}} }\:+\frac{{b}}{{u}−{u}_{\mathrm{2}} }\:+\frac{{cu}\:+{d}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:={lim}_{{u}\rightarrow{u}_{\mathrm{1}} } \left({u}−{u}_{\mathrm{1}} \right){F}\left({u}\right)\:=\frac{{u}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{1}}{{x}\left(\mathrm{2}\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}}\right)\left({u}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{{u}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\left({u}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${b}\:={lim}_{{u}\rightarrow{u}_{\mathrm{2}} } \left({u}−{u}_{\mathrm{2}} \right){F}\left({u}\right)\:=\frac{{u}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{1}}{{x}\left(−\mathrm{2}\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}}\right)\left({u}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{{u}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{1}}{−\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\left({u}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${lim}_{{u}\rightarrow+\infty} {uF}\left({u}\right)\:=\mathrm{0}\:={a}+{b}\:+{c}\:\Rightarrow{c}\:=−\left({a}+{b}\right) \\ $$$${F}\left(\mathrm{0}\right)=\frac{\mathrm{1}}{{x}}\:=−\frac{{a}}{{u}_{\mathrm{1}} }−\frac{{b}}{{u}_{\mathrm{2}} }\:+{d}\:\Rightarrow{d}\:=\frac{\mathrm{1}}{{x}}+\frac{{a}}{{u}_{\mathrm{1}} }\:+\frac{{b}}{{u}_{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:{F}\left({u}\right){du}\:=\left[{aln}\mid{u}−{u}_{\mathrm{1}} \mid+{bln}\mid{u}−{u}_{\mathrm{2}} \mid\right]_{\mathrm{1}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:+\left[\frac{{c}}{\mathrm{2}}{ln}\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)+{darctan}\left({u}\right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$$\left.={aln}\mid\frac{\sqrt{\mathrm{2}}−\mathrm{1}−{u}_{\mathrm{1}} }{\mathrm{1}−{u}_{\mathrm{1}} }\mid+{bln}\mid\frac{\sqrt{\mathrm{2}}−\mathrm{1}−{u}_{\mathrm{2}} }{\mathrm{1}−{u}_{\mathrm{2}} }\mid+\frac{{c}}{\mathrm{2}}{ln}\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{1}\right)+{d}\:{arctan}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\right\} \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{2}{aln}\mid\frac{\sqrt{\mathrm{2}}−\mathrm{1}−{u}_{\mathrm{1}} }{\mathrm{1}−{u}_{\mathrm{1}} }\mid+\mathrm{2}{bln}\mid\frac{\sqrt{\mathrm{2}}−\mathrm{1}−{u}_{\mathrm{2}} }{\mathrm{1}−{u}_{\mathrm{2}} }\mid+{cln}\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}\right)+\frac{{d}\pi}{\mathrm{4}} \\ $$$${a}\:=\frac{\left(\frac{\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}}\right)^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\left(\left(\frac{\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}}\right)^{\mathrm{2}} +\mathrm{1}\right)}\:=\frac{\left(\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} −{x}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\left(\left(\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{1}+{x}^{\mathrm{2}} −{x}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{1}+{x}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)}\:=\frac{\left(\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\left(\mathrm{2}+\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{2}{x}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\left({x}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{1}\right)}\:\:{rest}\:{to}\:{simplify}\:{other}\:{coefficie}\mathrm{7}{ts}… \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 10/Aug/19
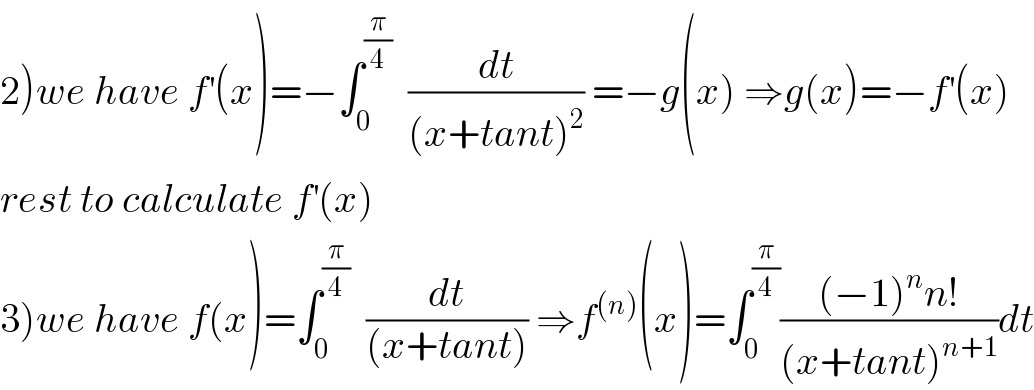
$$\left.\mathrm{2}\right){we}\:{have}\:{f}^{'} \left({x}\right)=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dt}}{\left({x}+{tant}\right)^{\mathrm{2}} }\:=−{g}\left({x}\right)\:\Rightarrow{g}\left({x}\right)=−{f}^{'} \left({x}\right) \\ $$$${rest}\:{to}\:{calculate}\:{f}^{'} \left({x}\right) \\ $$$$\left.\mathrm{3}\right){we}\:{have}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dt}}{\left({x}+{tant}\right)}\:\Rightarrow{f}^{\left({n}\right)} \left({x}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left({x}+{tant}\right)^{{n}+\mathrm{1}} }{dt} \\ $$
Commented by mathmax by abdo last updated on 10/Aug/19
![4) changement tan((t/2))=u give ∫_0 ^(π/4) (dt/((2+tant))) =∫_0 ^((√2)−1) (1/(2+((2u)/(1−u^2 ))))((2du)/(1+u^2 )) =2 ∫_0 ^((√2)−1) ((1−u^2 )/((1+u^2 )(2−2u^2 +2u))) =2 ∫_0 ^((√2)−1) ((u^2 −1)/((u^2 +1)(2u^2 −2u−2))) =∫_0 ^((√2)−1) ((u^2 −1)/((u^2 −u−1)(u^2 +1)))du let decompose F(u) =((u^2 −1)/((u^2 −u−1)(u^2 +1))) u^2 −u−1=0→Δ =1+4 =5 ⇒u_1 =((1+(√5))/2) and u_2 =((1−(√5))/2) F(u)=((u^2 −1)/((u−u_1 )(u−u_2 )(u^2 +1))) =(a/(u−u_1 )) +(b/(u−u_2 )) +((cu +d)/(u^2 +1)) a =((u_1 ^2 −1)/( (√5)(u_1 ^2 +1))) =(((((1+(√5))^2 )/4)−1)/( (√5)( (((1+(√5))^2 )/4)+1))) =((6+2(√5)−4)/( (√5)(6+2(√5)+4))) =((2+2(√5))/( (√5)(10+2(√5)))) =((1+(√5))/( (√5)(5+(√5)))) =((1+(√5))/(5(√5)+5)) =(1/5) b =((u_2 ^2 −1)/(−(√5)(u_2 ^2 +1))) =(((((1−(√5))^2 )/4)−1)/((−(√5))((((1−(√5))^2 )/4)+1))) =((6−2(√5)−4)/((−(√5))(6−2(√5)+4))) =((2−2(√5))/((−(√5))(10−2(√5)))) =((1−(√5))/((−(√5))(5−(√5)))) =(((√5)−1)/(5(√5)−5)) =(1/5) lim_(u→+∞) uF(u)=0 =a+b+c ⇒c =−(2/5) F(0) =1 =−(a/u_1 )−(b/u_2 ) +d ⇒d =1+(1/(5u_1 )) +(1/(5u_2 )) =1+(1/5){((u_1 +u_2 )/(u_1 u_2 ))} =1+(1/5) (1/(−1)) =1−(1/5) =(4/5) ⇒ F(u)= (1/(5(u−u_1 ))) +(1/(5(u−u_2 ))) +((((−2)/5)u +(4/5))/(u^2 +1)) ⇒ ∫ F(u)du =(1/5)ln∣u−u_1 ∣+(1/5)ln∣u−u_2 ∣−(1/5)ln(u^2 +1)+(4/5) arctanu +c ⇒ ∫_0 ^((√2)−1) F(u)du= [(1/5)ln∣u−u_1 ∣+(1/5)ln∣u−u_2 ∣−(1/5)ln(u^2 +1)+(4/5)arctan(u)]_0 ^((√2)−1) ...rest to finish the calculus...](https://www.tinkutara.com/question/Q66198.png)
$$\left.\mathrm{4}\right)\:{changement}\:{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}\:{give}\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{dt}}{\left(\mathrm{2}+{tant}\right)}\:=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{2}{u}}{\mathrm{1}−{u}^{\mathrm{2}} }}\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{2}−\mathrm{2}{u}^{\mathrm{2}} \:+\mathrm{2}{u}\right)} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\frac{{u}^{\mathrm{2}} −\mathrm{1}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{2}{u}^{\mathrm{2}} −\mathrm{2}{u}−\mathrm{2}\right)}\:=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{{u}^{\mathrm{2}} −\mathrm{1}}{\left({u}^{\mathrm{2}} −{u}−\mathrm{1}\right)\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)}{du} \\ $$$${let}\:{decompose}\:{F}\left({u}\right)\:=\frac{{u}^{\mathrm{2}} −\mathrm{1}}{\left({u}^{\mathrm{2}} −{u}−\mathrm{1}\right)\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${u}^{\mathrm{2}} −{u}−\mathrm{1}=\mathrm{0}\rightarrow\Delta\:=\mathrm{1}+\mathrm{4}\:=\mathrm{5}\:\Rightarrow{u}_{\mathrm{1}} =\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\:{and}\:{u}_{\mathrm{2}} =\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${F}\left({u}\right)=\frac{{u}^{\mathrm{2}} −\mathrm{1}}{\left({u}−{u}_{\mathrm{1}} \right)\left({u}−{u}_{\mathrm{2}} \right)\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{{a}}{{u}−{u}_{\mathrm{1}} }\:+\frac{{b}}{{u}−{u}_{\mathrm{2}} }\:+\frac{{cu}\:+{d}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:=\frac{{u}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{\mathrm{5}}\left({u}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{\frac{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }{\mathrm{4}}−\mathrm{1}}{\:\sqrt{\mathrm{5}}\left(\:\frac{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }{\mathrm{4}}+\mathrm{1}\right)}\:=\frac{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}−\mathrm{4}}{\:\sqrt{\mathrm{5}}\left(\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}+\mathrm{4}\right)}\:=\frac{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{5}}\left(\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}\right)} \\ $$$$=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{5}}\left(\mathrm{5}+\sqrt{\mathrm{5}}\right)}\:=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{5}\sqrt{\mathrm{5}}+\mathrm{5}}\:=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${b}\:=\frac{{u}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{1}}{−\sqrt{\mathrm{5}}\left({u}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{\frac{\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }{\mathrm{4}}−\mathrm{1}}{\left(−\sqrt{\mathrm{5}}\right)\left(\frac{\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }{\mathrm{4}}+\mathrm{1}\right)}\:=\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}−\mathrm{4}}{\left(−\sqrt{\mathrm{5}}\right)\left(\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}+\mathrm{4}\right)} \\ $$$$=\frac{\mathrm{2}−\mathrm{2}\sqrt{\mathrm{5}}}{\left(−\sqrt{\mathrm{5}}\right)\left(\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}\right)}\:=\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\left(−\sqrt{\mathrm{5}}\right)\left(\mathrm{5}−\sqrt{\mathrm{5}}\right)}\:=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{5}\sqrt{\mathrm{5}}−\mathrm{5}}\:=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${lim}_{{u}\rightarrow+\infty} {uF}\left({u}\right)=\mathrm{0}\:={a}+{b}+{c}\:\Rightarrow{c}\:=−\frac{\mathrm{2}}{\mathrm{5}} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{1}\:=−\frac{{a}}{{u}_{\mathrm{1}} }−\frac{{b}}{{u}_{\mathrm{2}} }\:+{d}\:\Rightarrow{d}\:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{5}{u}_{\mathrm{1}} }\:+\frac{\mathrm{1}}{\mathrm{5}{u}_{\mathrm{2}} } \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{5}}\left\{\frac{{u}_{\mathrm{1}} +{u}_{\mathrm{2}} }{{u}_{\mathrm{1}} {u}_{\mathrm{2}} }\right\}\:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{5}}\:\frac{\mathrm{1}}{−\mathrm{1}}\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}\:=\frac{\mathrm{4}}{\mathrm{5}}\:\Rightarrow \\ $$$${F}\left({u}\right)=\:\frac{\mathrm{1}}{\mathrm{5}\left({u}−{u}_{\mathrm{1}} \right)}\:+\frac{\mathrm{1}}{\mathrm{5}\left({u}−{u}_{\mathrm{2}} \right)}\:+\frac{\frac{−\mathrm{2}}{\mathrm{5}}{u}\:+\frac{\mathrm{4}}{\mathrm{5}}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:{F}\left({u}\right){du}\:=\frac{\mathrm{1}}{\mathrm{5}}{ln}\mid{u}−{u}_{\mathrm{1}} \mid+\frac{\mathrm{1}}{\mathrm{5}}{ln}\mid{u}−{u}_{\mathrm{2}} \mid−\frac{\mathrm{1}}{\mathrm{5}}{ln}\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)+\frac{\mathrm{4}}{\mathrm{5}}\:{arctanu}\:+{c} \\ $$$$\Rightarrow\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:{F}\left({u}\right){du}= \\ $$$$\left[\frac{\mathrm{1}}{\mathrm{5}}{ln}\mid{u}−{u}_{\mathrm{1}} \mid+\frac{\mathrm{1}}{\mathrm{5}}{ln}\mid{u}−{u}_{\mathrm{2}} \mid−\frac{\mathrm{1}}{\mathrm{5}}{ln}\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)+\frac{\mathrm{4}}{\mathrm{5}}{arctan}\left({u}\right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$$…{rest}\:{to}\:{finish}\:{the}\:{calculus}… \\ $$
