Question Number 67744 by mathmax by abdo last updated on 31/Aug/19
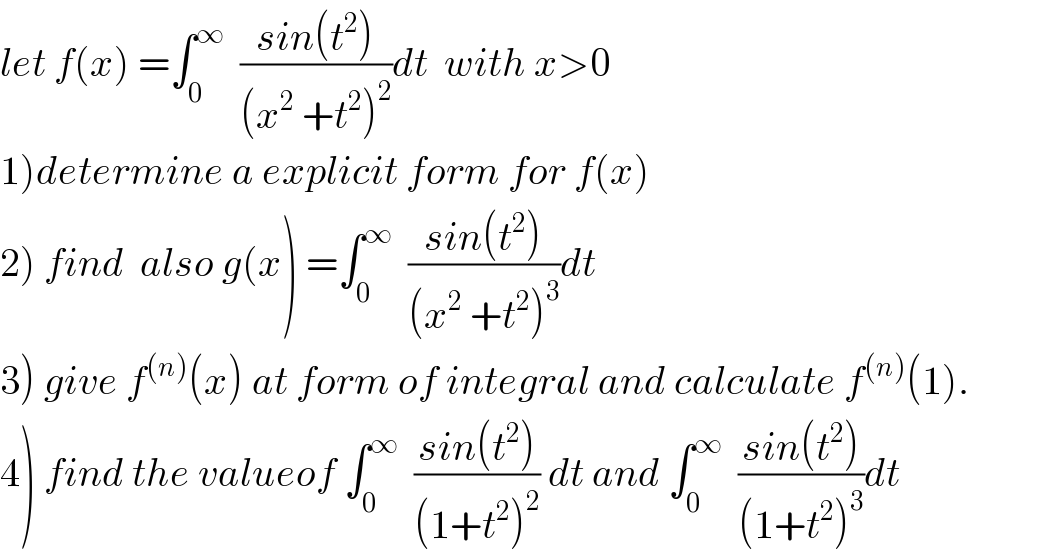
Commented by mathmax by abdo last updated on 31/Aug/19

Commented by mathmax by abdo last updated on 31/Aug/19
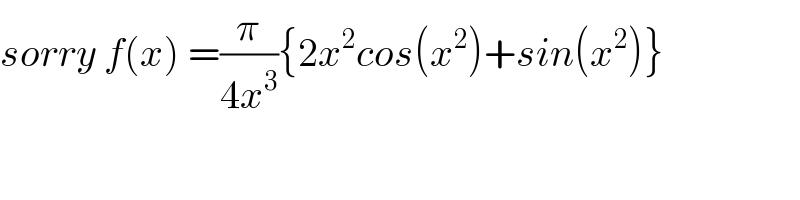
Commented by mathmax by abdo last updated on 31/Aug/19
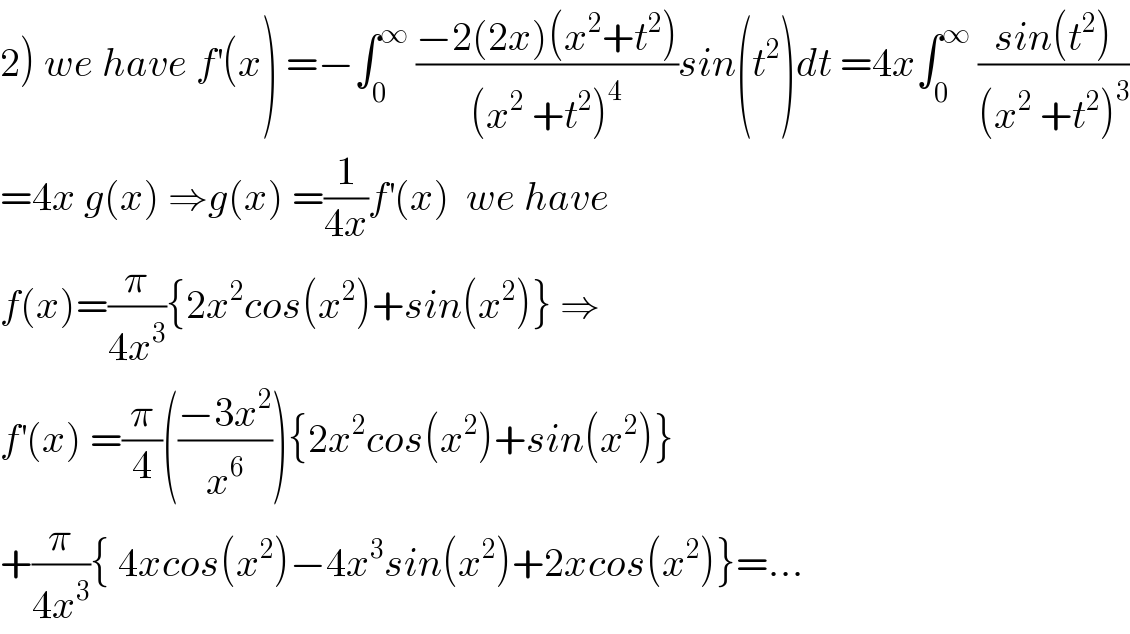
Commented by mathmax by abdo last updated on 31/Aug/19

