let-f-x-and-g-x-be-twice-differentiable-functions-on-0-2-satisfying-f-x-g-x-f-1-4-g-1-6-f-2-3-and-g-2-9-Then-what-is-f-x-g-x-at-x-4-equal-to-

Question Number 10039 by Gaurav3651 last updated on 21/Jan/17

$$ \\ $$$${let}\:{f}\left({x}\right)\:{and}\:{g}\left({x}\right)\:{be}\:{twice}\:{differentiable} \\ $$$${functions}\:{on}\:\left[\mathrm{0},\mathrm{2}\right]\:{satisfying} \\ $$$${f}''\left({x}\right)={g}''\left({x}\right),\:{f}'\left(\mathrm{1}\right)=\mathrm{4},\:{g}'\left(\mathrm{1}\right)=\mathrm{6}, \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{3}\:{and}\:{g}\left(\mathrm{2}\right)=\mathrm{9}.\:{Then}\:{what}\:{is} \\ $$$${f}\left({x}\right)−{g}\left({x}\right)\:{at}\:{x}=\mathrm{4}\:{equal}\:{to}? \\ $$

Commented by prakash jain last updated on 22/Jan/17

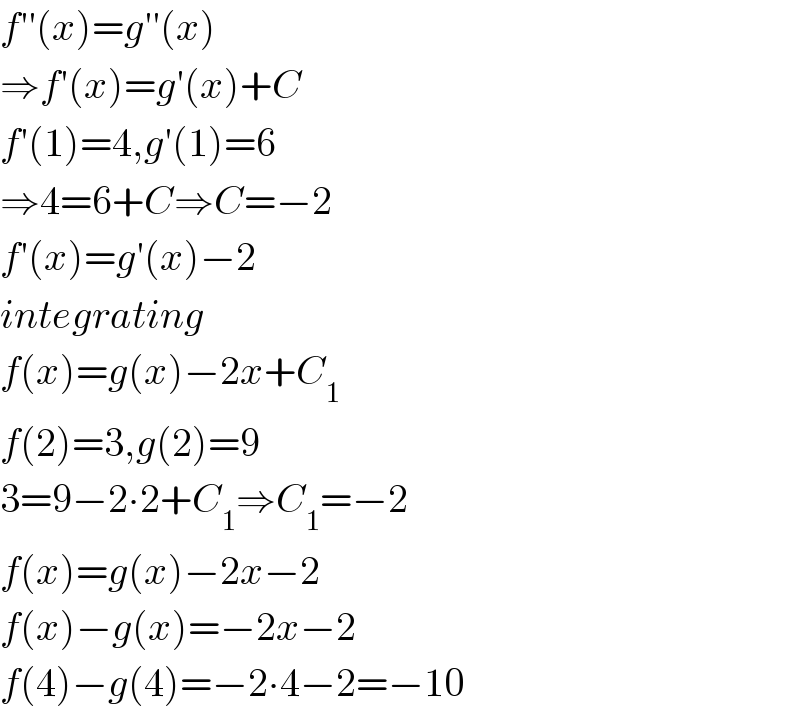
$${f}''\left({x}\right)={g}''\left({x}\right) \\ $$$$\Rightarrow{f}'\left({x}\right)={g}'\left({x}\right)+{C} \\ $$$${f}'\left(\mathrm{1}\right)=\mathrm{4},{g}'\left(\mathrm{1}\right)=\mathrm{6} \\ $$$$\Rightarrow\mathrm{4}=\mathrm{6}+{C}\Rightarrow{C}=−\mathrm{2} \\ $$$${f}'\left({x}\right)={g}'\left({x}\right)−\mathrm{2} \\ $$$${integrating} \\ $$$${f}\left({x}\right)={g}\left({x}\right)−\mathrm{2}{x}+{C}_{\mathrm{1}} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{3},{g}\left(\mathrm{2}\right)=\mathrm{9} \\ $$$$\mathrm{3}=\mathrm{9}−\mathrm{2}\centerdot\mathrm{2}+{C}_{\mathrm{1}} \Rightarrow{C}_{\mathrm{1}} =−\mathrm{2} \\ $$$${f}\left({x}\right)={g}\left({x}\right)−\mathrm{2}{x}−\mathrm{2} \\ $$$${f}\left({x}\right)−{g}\left({x}\right)=−\mathrm{2}{x}−\mathrm{2} \\ $$$${f}\left(\mathrm{4}\right)−{g}\left(\mathrm{4}\right)=−\mathrm{2}\centerdot\mathrm{4}−\mathrm{2}=−\mathrm{10} \\ $$

Commented by mrW1 last updated on 22/Jan/17

$$\mathcal{GREAT} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com