Question Number 12302 by Gaurav3651 last updated on 18/Apr/17
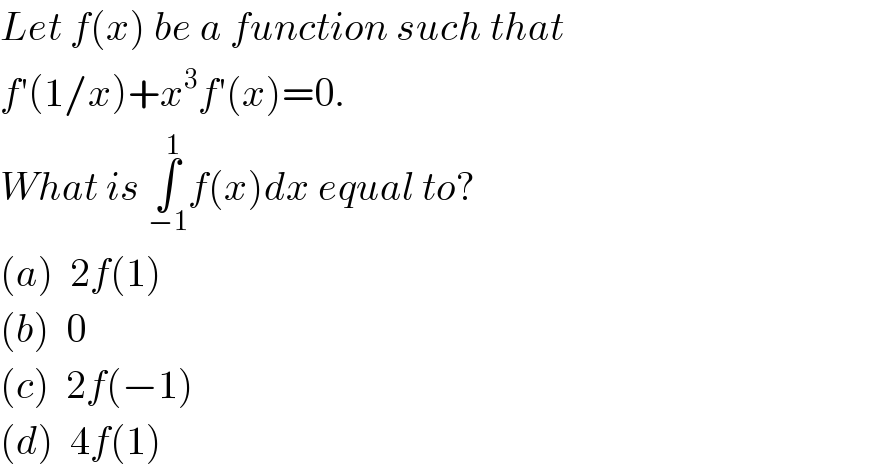
$${Let}\:{f}\left({x}\right)\:{be}\:{a}\:{function}\:{such}\:{that} \\ $$$${f}'\left(\mathrm{1}/{x}\right)+{x}^{\mathrm{3}} {f}'\left({x}\right)=\mathrm{0}. \\ $$$${What}\:{is}\:\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}{f}\left({x}\right){dx}\:{equal}\:{to}? \\ $$$$\left({a}\right)\:\:\mathrm{2}{f}\left(\mathrm{1}\right) \\ $$$$\left({b}\right)\:\:\mathrm{0} \\ $$$$\left({c}\right)\:\:\mathrm{2}{f}\left(−\mathrm{1}\right) \\ $$$$\left({d}\right)\:\:\mathrm{4}{f}\left(\mathrm{1}\right) \\ $$
Answered by mrW1 last updated on 18/Apr/17
![f′(1/x)=−x^3 f′(x) −(1/x^2 )f′((1/x))=xf′(x) ∫[−(1/x^2 )f′((1/x))]dx=∫xf′(x)dx ∫f′((1/x))d((1/x))=∫xd[f(x)]+C f((1/x))=xf(x)−∫f(x)dx+C ⇒ ∫f(x)dx=xf(x)−f((1/x))+C ∫_(−1) ^1 f(x)dx=[xf(x)−f((1/x))]_(−1) ^1 =[1×f(1)−f(1)]−[−1×f(−1)−f(−1)] =2f(−1) ⇒ Answer (c)](https://www.tinkutara.com/question/Q12313.png)
$${f}'\left(\mathrm{1}/{x}\right)=−{x}^{\mathrm{3}} {f}'\left({x}\right) \\ $$$$−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{f}'\left(\frac{\mathrm{1}}{{x}}\right)={xf}'\left({x}\right) \\ $$$$\int\left[−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{f}'\left(\frac{\mathrm{1}}{{x}}\right)\right]{dx}=\int{xf}'\left({x}\right){dx} \\ $$$$\int{f}'\left(\frac{\mathrm{1}}{{x}}\right){d}\left(\frac{\mathrm{1}}{{x}}\right)=\int{xd}\left[{f}\left({x}\right)\right]+{C} \\ $$$${f}\left(\frac{\mathrm{1}}{{x}}\right)={xf}\left({x}\right)−\int{f}\left({x}\right){dx}+{C} \\ $$$$\Rightarrow\:\int{f}\left({x}\right){dx}={xf}\left({x}\right)−{f}\left(\frac{\mathrm{1}}{{x}}\right)+{C} \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{1}} {f}\left({x}\right){dx}=\left[{xf}\left({x}\right)−{f}\left(\frac{\mathrm{1}}{{x}}\right)\right]_{−\mathrm{1}} ^{\mathrm{1}} \\ $$$$=\left[\mathrm{1}×{f}\left(\mathrm{1}\right)−{f}\left(\mathrm{1}\right)\right]−\left[−\mathrm{1}×{f}\left(−\mathrm{1}\right)−{f}\left(−\mathrm{1}\right)\right] \\ $$$$=\mathrm{2}{f}\left(−\mathrm{1}\right) \\ $$$$ \\ $$$$\Rightarrow\:{Answer}\:\left({c}\right) \\ $$
