Menu Close

let-g-x-ln-1-x-3-x-2-1-find-g-n-x-and-g-n-0-2-developp-g-at-integr-serie-

Tinku Tara 0 Comments
Pin




Question Number 72394 by mathmax by abdo last updated on 28/Oct/19
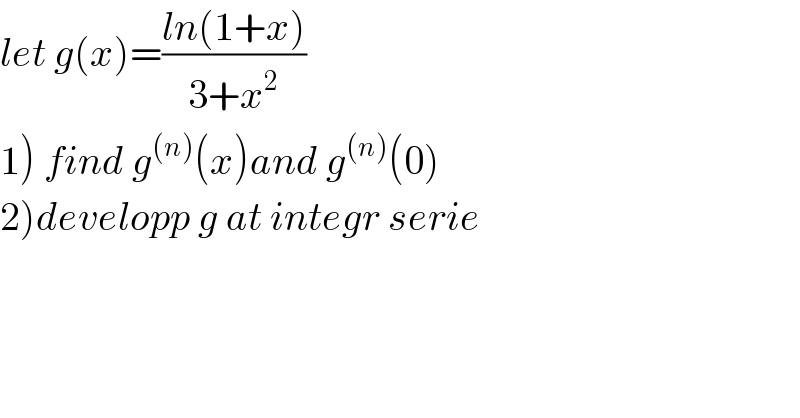
let g(x)=((ln(1+x))/(3+x^2 )) 1) find g^((n)) (x)and g^((n)) (0) 2)developp g at integr serie
$${let}\:{g}\left({x}\right)=\frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{3}+{x}^{\mathrm{2}} } \\ $$$$\left.\mathrm{1}\right)\:{find}\:{g}^{\left({n}\right)} \left({x}\right){and}\:{g}^{\left({n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right){developp}\:{g}\:{at}\:{integr}\:{serie} \\ $$
Commented by mathmax by abdo last updated on 29/Oct/19
1) we have g^((n)) (x)=Σ_(k=0) ^n C_n ^k (ln(1+x))^((k)) ((1/(x^2 +3)))^((n−k)) but ln(x+1))^((1)) =(1/(x+1)) ⇒(ln(x+1))^((k)) =((1/(x+1)))^((k−1)) =(((−1)^(k−1) (k−1)!)/((x+1)^k )) we have (1/(x^2 +3)) =(1/((x−i(√3))(x+i(√3)))) =(1/(2i(√3)))((1/(x−i(√3)))−(1/(x+i(√3)))) ⇒ ((1/(x^2 +3)))^((n−k)) =(1/(2i(√3))){ ((1/(x−i(√3))))^((n−k)) −((1/(x+i(√3))))^((n−k)) } =(1/(2i(√3))){(((−1)^(n−k) (n−k)!)/((x−i(√3))^(n−k+1) ))−(((−1)^(n−k) (n−k)!)/((x+i(√3))^(n−k+1) ))} =(((−1)^(n−k) (n−k)!)/(2i(√3))){(((x+i(√3))^(n−k+1) −(x−i(√3))^(n−k+1) )/((x^2 +3)^(n−k+1) ))} =(((−1)^(n−k) (n−k)!)/( (√3)))×((Im(x+i(√3))^(n−k+1) )/((x^2 +3)^(n−k+1) )) ⇒ g^((n)) (x)=ln(1+x)((1/(x^2 +3)))^((n)) +Σ_(k=1) ^n ((n!)/(k!(n−k)!)) (((−1)^(k−1) (k−1)!)/((x+1)^k ))×(((−1)^(n−k) (n−k)!×Im(x+i(√3))^(n−k+1) )/( (√3)(x^2 +3)^(n−k+1) )) g^((n)) (x)=ln(x+1)((1/(x^2 +3)))^((n)) +Σ_(k=1) ^n ((n!(−1)^(n−1) .Im(x+i(√3))^(n−k+1) )/(k(√3)(x+1)^k (x^2 +3)^(n−k+1) )) also we have ((1/(x^2 +3)))^((n)) =(1/(2i(√3))){ ((1/(x−i(√3))))^((n)) −((1/(x+i(√3))))^((n)) } =(1/(2i(√3))){ (((−1)^n n!)/((x−i(√3))^(n+1) ))−(((−1)^n n!)/((x+i(√3))^(n+1) ))} =(((−1)^n n!)/(2i(√3))){((2iIm(x+i(√3))^(n+1) )/((x^2 +3)^(n+1) ))} =(((−1)^n n!)/( (√3)))×((Im(x+i(√3))^(n+1) )/((x^2 +3)^(n+1) )) ⇒ g^((n)) (x)=(((−1)^n n!)/( (√3)))×((Im(x+i(√3))^(n+1) )/((x^2 +3)^(n+1) ))ln(x+1) +Σ_(k=1) ^n ((n!(−1)^(n−1) ×Im(x+i(√3))^(n−k+1) )/(k(√3)(x+1)^k (x^2 +3)^(n−k+1) )).
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{g}^{\left({n}\right)} \left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \left({ln}\left(\mathrm{1}+{x}\right)\right)^{\left({k}\right)} \left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{3}}\right)^{\left({n}−{k}\right)} \\ $$$$\left.{but}\:{ln}\left({x}+\mathrm{1}\right)\right)^{\left(\mathrm{1}\right)} =\frac{\mathrm{1}}{{x}+\mathrm{1}}\:\Rightarrow\left({ln}\left({x}+\mathrm{1}\right)\right)^{\left({k}\right)} =\left(\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)^{\left({k}−\mathrm{1}\right)} =\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!}{\left({x}+\mathrm{1}\right)^{{k}} } \\ $$$${we}\:{have}\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{3}}\:=\frac{\mathrm{1}}{\left({x}−{i}\sqrt{\mathrm{3}}\right)\left({x}+{i}\sqrt{\mathrm{3}}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\left(\frac{\mathrm{1}}{{x}−{i}\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{{x}+{i}\sqrt{\mathrm{3}}}\right)\:\Rightarrow \\ $$$$\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{3}}\right)^{\left({n}−{k}\right)} =\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\left\{\:\left(\frac{\mathrm{1}}{{x}−{i}\sqrt{\mathrm{3}}}\right)^{\left({n}−{k}\right)} −\left(\frac{\mathrm{1}}{{x}+{i}\sqrt{\mathrm{3}}}\right)^{\left({n}−{k}\right)} \right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\left\{\frac{\left(−\mathrm{1}\right)^{{n}−{k}} \left({n}−{k}\right)!}{\left({x}−{i}\sqrt{\mathrm{3}}\right)^{{n}−{k}+\mathrm{1}} }−\frac{\left(−\mathrm{1}\right)^{{n}−{k}} \left({n}−{k}\right)!}{\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}−{k}+\mathrm{1}} }\right\} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}−{k}} \left({n}−{k}\right)!}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\left\{\frac{\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}−{k}+\mathrm{1}} −\left({x}−{i}\sqrt{\mathrm{3}}\right)^{{n}−{k}+\mathrm{1}} }{\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{{n}−{k}+\mathrm{1}} }\right\} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}−{k}} \left({n}−{k}\right)!}{\:\sqrt{\mathrm{3}}}×\frac{{Im}\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}−{k}+\mathrm{1}} }{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)^{{n}−{k}+\mathrm{1}} }\:\Rightarrow \\ $$$${g}^{\left({n}\right)} \left({x}\right)={ln}\left(\mathrm{1}+{x}\right)\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{3}}\right)^{\left({n}\right)} \: \\ $$$$+\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{n}!}{{k}!\left({n}−{k}\right)!}\:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left({k}−\mathrm{1}\right)!}{\left({x}+\mathrm{1}\right)^{{k}} }×\frac{\left(−\mathrm{1}\right)^{{n}−{k}} \left({n}−{k}\right)!×{Im}\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}−{k}+\mathrm{1}} }{\:\sqrt{\mathrm{3}}\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{{n}−{k}+\mathrm{1}} } \\ $$$${g}^{\left({n}\right)} \left({x}\right)={ln}\left({x}+\mathrm{1}\right)\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{3}}\right)^{\left({n}\right)} \\ $$$$+\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\:\frac{{n}!\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:.{Im}\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}−{k}+\mathrm{1}} }{{k}\sqrt{\mathrm{3}}\left({x}+\mathrm{1}\right)^{{k}} \left({x}^{\mathrm{2}} +\mathrm{3}\right)^{{n}−{k}+\mathrm{1}} }\:\:{also}\:{we}\:{have} \\ $$$$\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{3}}\right)^{\left({n}\right)} =\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\left\{\:\left(\frac{\mathrm{1}}{{x}−{i}\sqrt{\mathrm{3}}}\right)^{\left({n}\right)} −\left(\frac{\mathrm{1}}{{x}+{i}\sqrt{\mathrm{3}}}\right)^{\left({n}\right)} \right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\left\{\:\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left({x}−{i}\sqrt{\mathrm{3}}\right)^{{n}+\mathrm{1}} }−\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}+\mathrm{1}} }\right\} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\left\{\frac{\mathrm{2}{iIm}\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}+\mathrm{1}} }{\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{{n}+\mathrm{1}} }\right\}\:=\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\:\sqrt{\mathrm{3}}}×\frac{{Im}\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}+\mathrm{1}} }{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)^{{n}+\mathrm{1}} }\:\Rightarrow \\ $$$${g}^{\left({n}\right)} \left({x}\right)=\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\:\sqrt{\mathrm{3}}}×\frac{{Im}\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}+\mathrm{1}} }{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)^{{n}+\mathrm{1}} }{ln}\left({x}+\mathrm{1}\right) \\ $$$$+\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{{n}!\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} ×{Im}\left({x}+{i}\sqrt{\mathrm{3}}\right)^{{n}−{k}+\mathrm{1}} }{{k}\sqrt{\mathrm{3}}\left({x}+\mathrm{1}\right)^{{k}} \left({x}^{\mathrm{2}} \:+\mathrm{3}\right)^{{n}−{k}+\mathrm{1}} }. \\ $$
Commented by mathmax by abdo last updated on 29/Oct/19
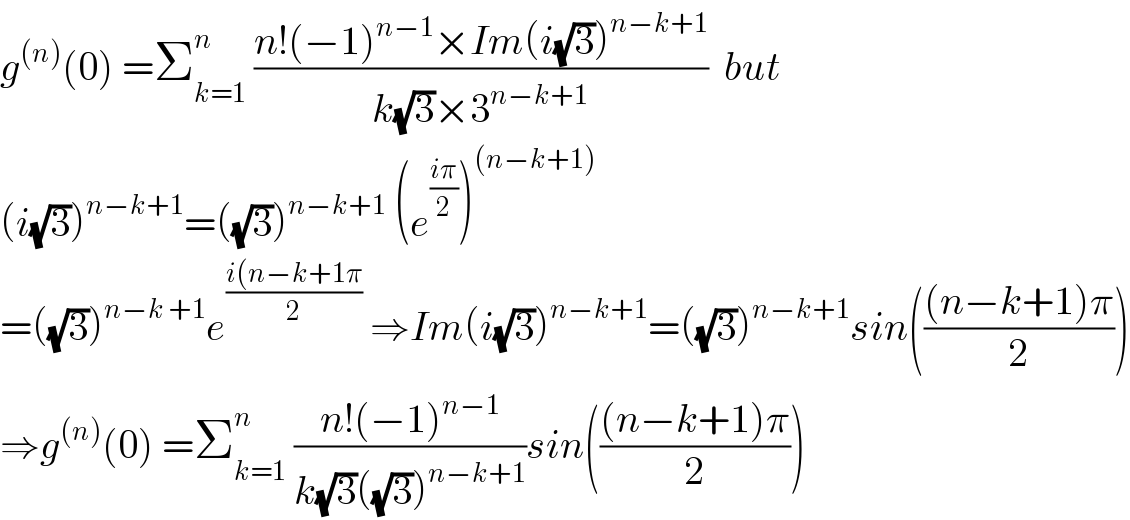
g^((n)) (0) =Σ_(k=1) ^n ((n!(−1)^(n−1) ×Im(i(√3))^(n−k+1) )/(k(√3)×3^(n−k+1) )) but (i(√3))^(n−k+1) =((√3))^(n−k+1) (e^((iπ)/2) )^((n−k+1)) =((√3))^(n−k +1) e^((i(n−k+1π)/2) ⇒Im(i(√3))^(n−k+1) =((√3))^(n−k+1) sin((((n−k+1)π)/2)) ⇒g^((n)) (0) =Σ_(k=1) ^n ((n!(−1)^(n−1) )/(k(√3)((√3))^(n−k+1) ))sin((((n−k+1)π)/2))
$${g}^{\left({n}\right)} \left(\mathrm{0}\right)\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{n}!\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} ×{Im}\left({i}\sqrt{\mathrm{3}}\right)^{{n}−{k}+\mathrm{1}} }{{k}\sqrt{\mathrm{3}}×\mathrm{3}^{{n}−{k}+\mathrm{1}} }\:\:{but} \\ $$$$\left({i}\sqrt{\mathrm{3}}\right)^{{n}−{k}+\mathrm{1}} =\left(\sqrt{\mathrm{3}}\right)^{{n}−{k}+\mathrm{1}} \:\left({e}^{\frac{{i}\pi}{\mathrm{2}}} \right)^{\left({n}−{k}+\mathrm{1}\right)} \\ $$$$=\left(\sqrt{\mathrm{3}}\right)^{{n}−{k}\:+\mathrm{1}} {e}^{\frac{{i}\left({n}−{k}+\mathrm{1}\pi\right.}{\mathrm{2}}} \:\Rightarrow{Im}\left({i}\sqrt{\mathrm{3}}\right)^{{n}−{k}+\mathrm{1}} =\left(\sqrt{\mathrm{3}}\right)^{{n}−{k}+\mathrm{1}} {sin}\left(\frac{\left({n}−{k}+\mathrm{1}\right)\pi}{\mathrm{2}}\right) \\ $$$$\Rightarrow{g}^{\left({n}\right)} \left(\mathrm{0}\right)\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{n}!\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{k}\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}\right)^{{n}−{k}+\mathrm{1}} }{sin}\left(\frac{\left({n}−{k}+\mathrm{1}\right)\pi}{\mathrm{2}}\right) \\ $$
Commented by mathmax by abdo last updated on 29/Oct/19
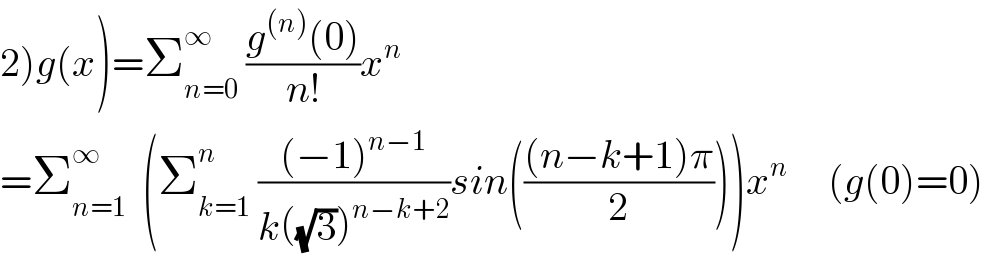
2)g(x)=Σ_(n=0) ^∞ ((g^((n)) (0))/(n!))x^n =Σ_(n=1) ^∞ (Σ_(k=1) ^n (((−1)^(n−1) )/(k((√3))^(n−k+2) ))sin((((n−k+1)π)/2)))x^n (g(0)=0)
$$\left.\mathrm{2}\right){g}\left({x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{g}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}{x}^{{n}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\left(\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{k}\left(\sqrt{\mathrm{3}}\right)^{{n}−{k}+\mathrm{2}} }{sin}\left(\frac{\left({n}−{k}+\mathrm{1}\right)\pi}{\mathrm{2}}\right)\right){x}^{{n}} \:\:\:\:\:\left({g}\left(\mathrm{0}\right)=\mathrm{0}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *