Question Number 4156 by Yozzii last updated on 30/Dec/15
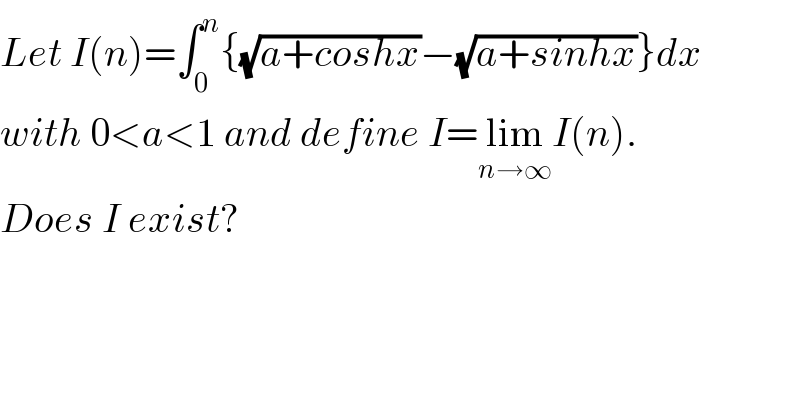
$${Let}\:{I}\left({n}\right)=\int_{\mathrm{0}} ^{{n}} \left\{\sqrt{{a}+{coshx}}−\sqrt{{a}+{sinhx}}\right\}{dx} \\ $$$${with}\:\mathrm{0}<{a}<\mathrm{1}\:{and}\:{define}\:{I}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}{I}\left({n}\right). \\ $$$${Does}\:{I}\:{exist}?\: \\ $$
Commented by 123456 last updated on 30/Dec/15
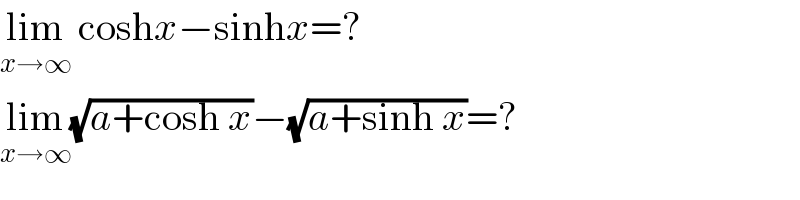
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{cosh}{x}−\mathrm{sinh}{x}=? \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt{{a}+\mathrm{cosh}\:{x}}−\sqrt{{a}+\mathrm{sinh}\:{x}}=? \\ $$
Commented by Yozzii last updated on 01/Jan/16
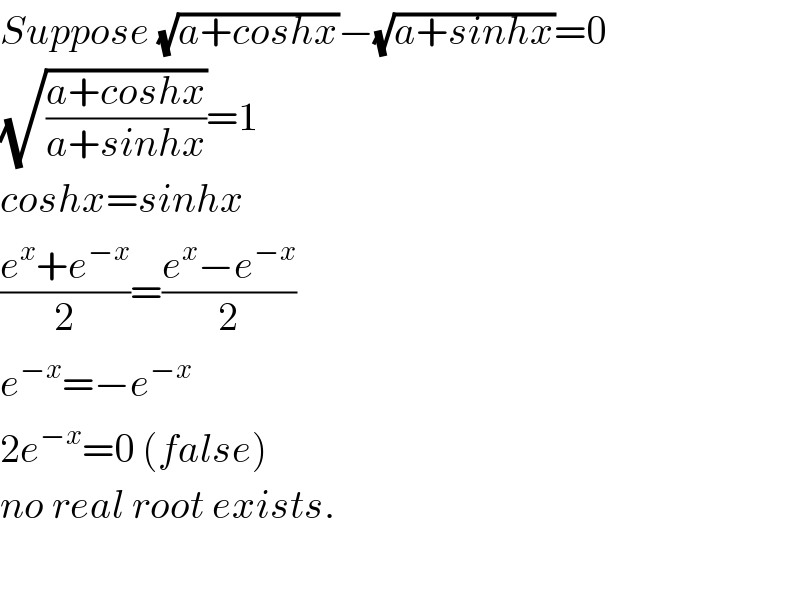
$${Suppose}\:\sqrt{{a}+{coshx}}−\sqrt{{a}+{sinhx}}=\mathrm{0} \\ $$$$\sqrt{\frac{{a}+{coshx}}{{a}+{sinhx}}}=\mathrm{1} \\ $$$${coshx}={sinhx} \\ $$$$\frac{{e}^{{x}} +{e}^{−{x}} }{\mathrm{2}}=\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}} \\ $$$${e}^{−{x}} =−{e}^{−{x}} \\ $$$$\mathrm{2}{e}^{−{x}} =\mathrm{0}\:\left({false}\right) \\ $$$${no}\:{real}\:{root}\:{exists}. \\ $$$$ \\ $$
Commented by Filup last updated on 31/Dec/15
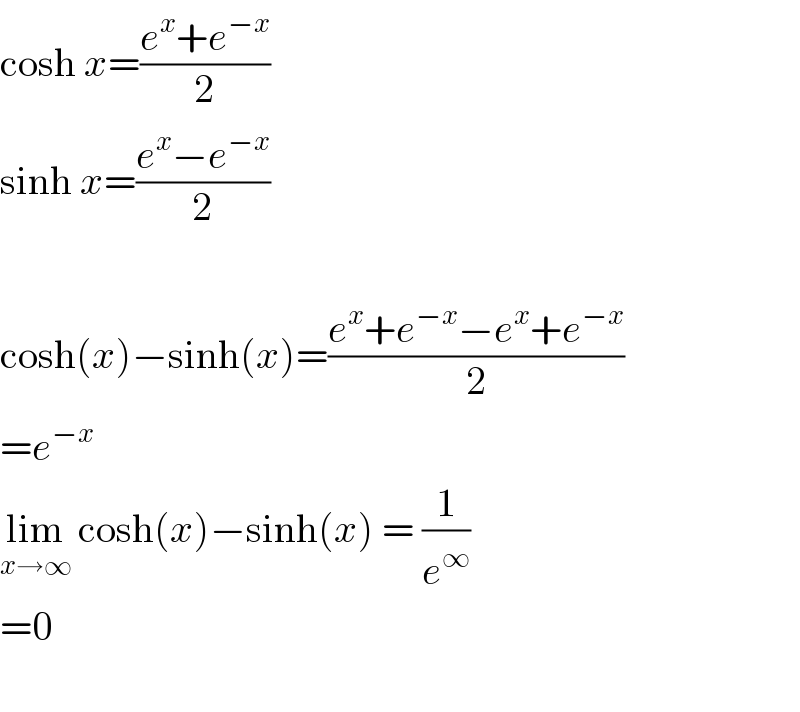
$$\mathrm{cosh}\:{x}=\frac{{e}^{{x}} +{e}^{−{x}} }{\mathrm{2}} \\ $$$$\mathrm{sinh}\:{x}=\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{cosh}\left({x}\right)−\mathrm{sinh}\left({x}\right)=\frac{{e}^{{x}} +{e}^{−{x}} −{e}^{{x}} +{e}^{−{x}} }{\mathrm{2}} \\ $$$$={e}^{−{x}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{cosh}\left({x}\right)−\mathrm{sinh}\left({x}\right)\:=\:\frac{\mathrm{1}}{{e}^{\infty} } \\ $$$$=\mathrm{0} \\ $$$$ \\ $$
Commented by Filup last updated on 31/Dec/15
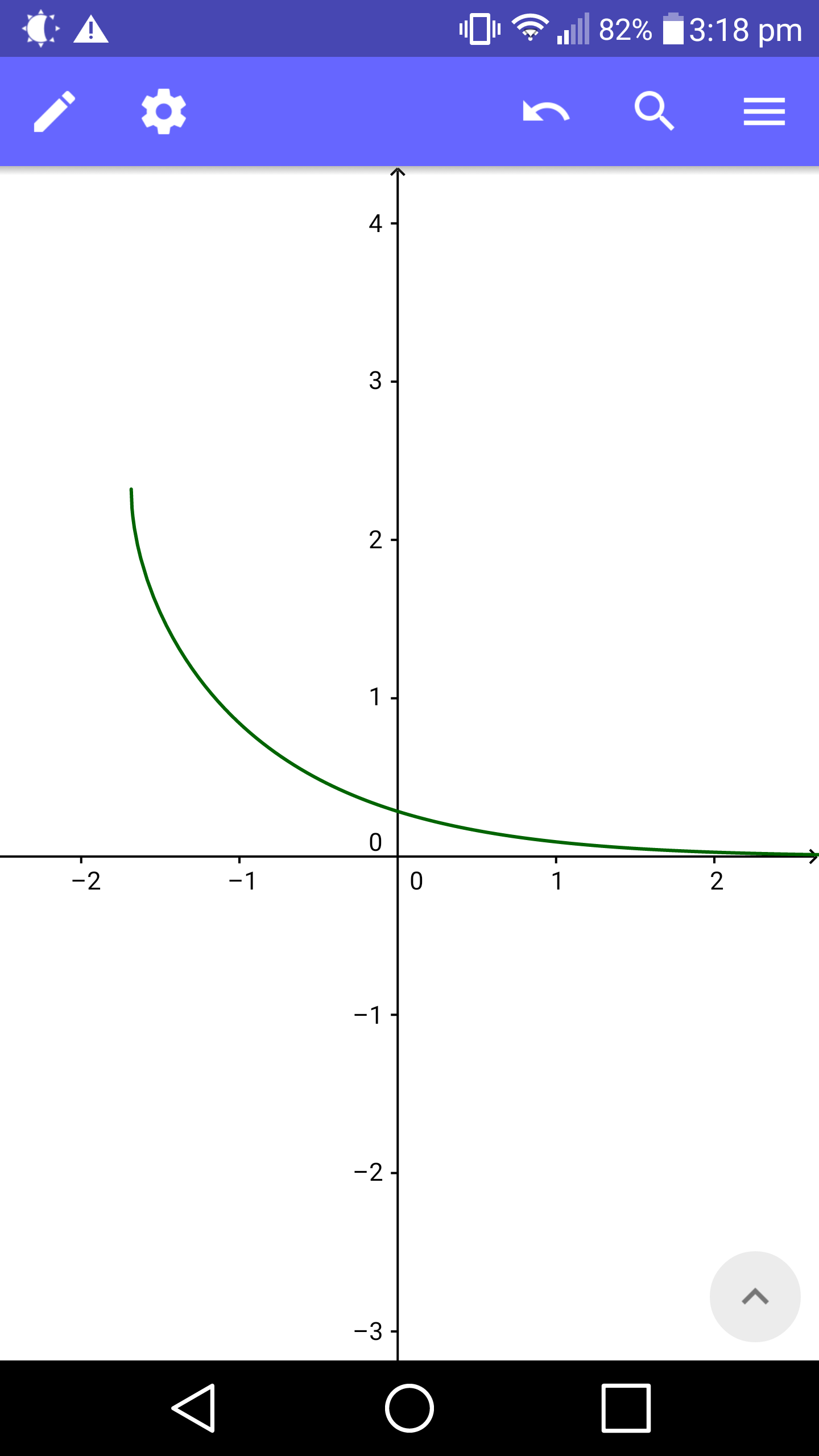
Commented by Filup last updated on 31/Dec/15
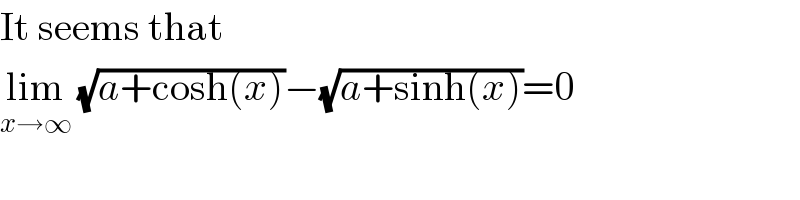
$$\mathrm{It}\:\mathrm{seems}\:\mathrm{that} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{{a}+\mathrm{cosh}\left({x}\right)}−\sqrt{{a}+\mathrm{sinh}\left({x}\right)}=\mathrm{0} \\ $$
Commented by Yozzii last updated on 31/Dec/15
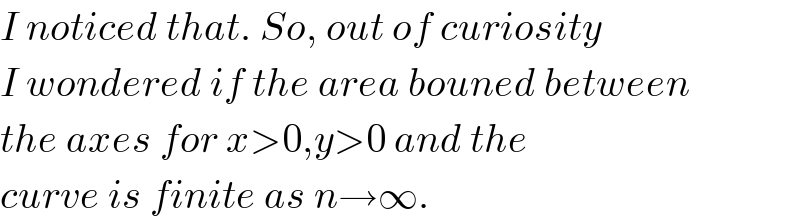
$${I}\:{noticed}\:{that}.\:{So},\:{out}\:{of}\:{curiosity} \\ $$$${I}\:{wondered}\:{if}\:{the}\:{area}\:{bouned}\:{between} \\ $$$${the}\:{axes}\:{for}\:{x}>\mathrm{0},{y}>\mathrm{0}\:{and}\:{the} \\ $$$${curve}\:{is}\:{finite}\:{as}\:{n}\rightarrow\infty. \\ $$
Commented by Yozzii last updated on 31/Dec/15
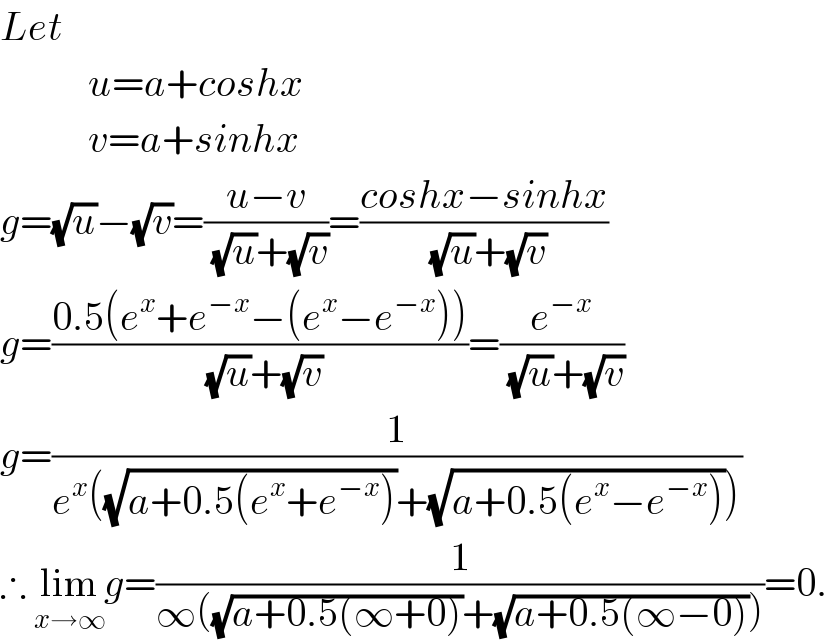
$${Let} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{u}={a}+{coshx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{v}={a}+{sinhx} \\ $$$${g}=\sqrt{{u}}−\sqrt{{v}}=\frac{{u}−{v}}{\:\sqrt{{u}}+\sqrt{{v}}}=\frac{{coshx}−{sinhx}}{\:\sqrt{{u}}+\sqrt{{v}}} \\ $$$${g}=\frac{\mathrm{0}.\mathrm{5}\left({e}^{{x}} +{e}^{−{x}} −\left({e}^{{x}} −{e}^{−{x}} \right)\right)}{\:\sqrt{{u}}+\sqrt{{v}}}=\frac{{e}^{−{x}} }{\:\sqrt{{u}}+\sqrt{{v}}} \\ $$$${g}=\frac{\mathrm{1}}{{e}^{{x}} \left(\sqrt{{a}+\mathrm{0}.\mathrm{5}\left({e}^{{x}} +{e}^{−{x}} \right)}+\sqrt{{a}+\mathrm{0}.\mathrm{5}\left({e}^{{x}} −{e}^{−{x}} \right)}\right)} \\ $$$$\therefore\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}{g}=\frac{\mathrm{1}}{\infty\left(\sqrt{{a}+\mathrm{0}.\mathrm{5}\left(\infty+\mathrm{0}\right)}+\sqrt{{a}+\mathrm{0}.\mathrm{5}\left(\infty−\mathrm{0}\right)}\right)}=\mathrm{0}. \\ $$
