Question Number 2186 by Yozzi last updated on 07/Nov/15
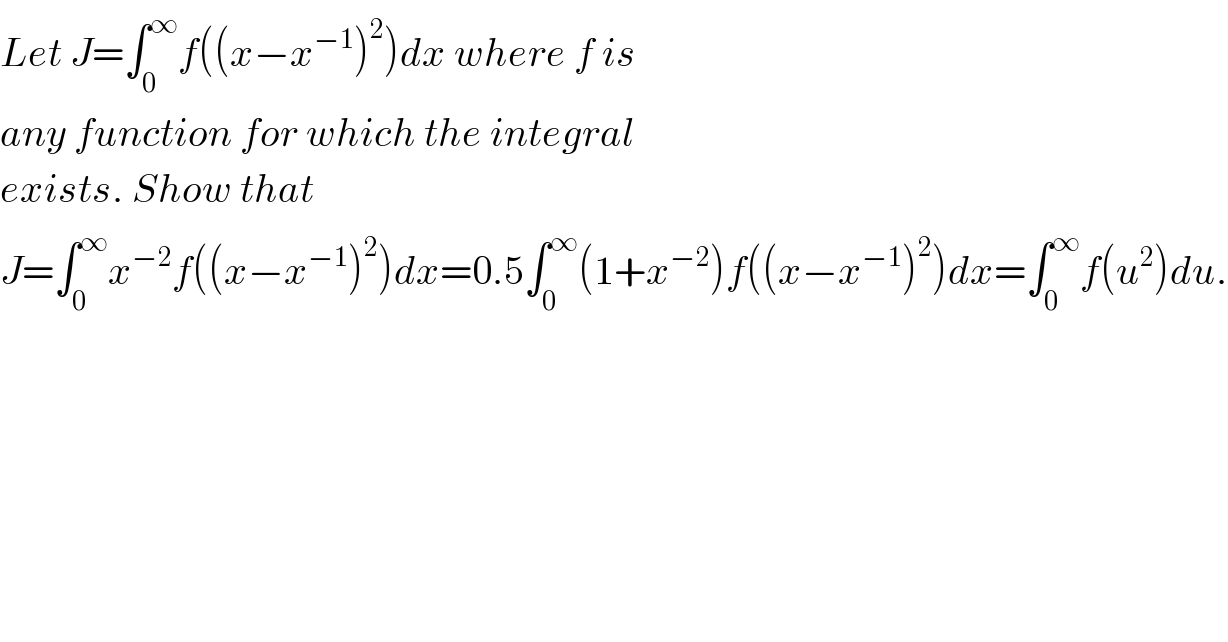
$${Let}\:{J}=\int_{\mathrm{0}} ^{\infty} {f}\left(\left({x}−{x}^{−\mathrm{1}} \right)^{\mathrm{2}} \right){dx}\:{where}\:{f}\:{is} \\ $$$${any}\:{function}\:{for}\:{which}\:{the}\:{integral} \\ $$$${exists}.\:{Show}\:{that} \\ $$$${J}=\int_{\mathrm{0}} ^{\infty} {x}^{−\mathrm{2}} {f}\left(\left({x}−{x}^{−\mathrm{1}} \right)^{\mathrm{2}} \right){dx}=\mathrm{0}.\mathrm{5}\int_{\mathrm{0}} ^{\infty} \left(\mathrm{1}+{x}^{−\mathrm{2}} \right){f}\left(\left({x}−{x}^{−\mathrm{1}} \right)^{\mathrm{2}} \right){dx}=\int_{\mathrm{0}} ^{\infty} {f}\left({u}^{\mathrm{2}} \right){du}. \\ $$$$ \\ $$
Answered by prakash jain last updated on 07/Nov/15
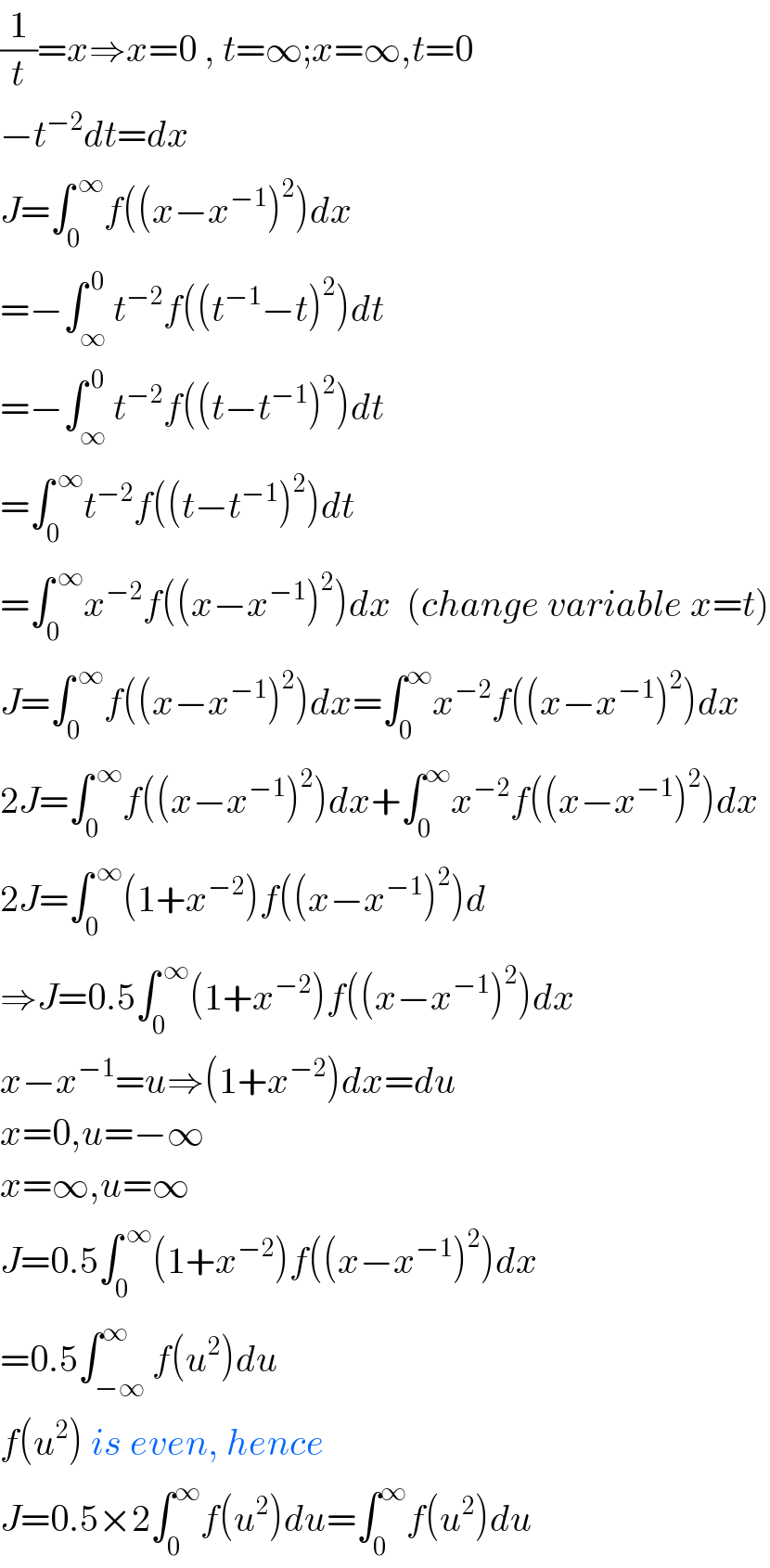
$$\frac{\mathrm{1}}{{t}}={x}\Rightarrow{x}=\mathrm{0}\:,\:{t}=\infty;{x}=\infty,{t}=\mathrm{0} \\ $$$$−{t}^{−\mathrm{2}} {dt}={dx} \\ $$$${J}=\int_{\mathrm{0}} ^{\:\infty} {f}\left(\left({x}−{x}^{−\mathrm{1}} \right)^{\mathrm{2}} \right){dx} \\ $$$$=−\int_{\infty} ^{\:\mathrm{0}} {t}^{−\mathrm{2}} {f}\left(\left({t}^{−\mathrm{1}} −{t}\right)^{\mathrm{2}} \right){dt} \\ $$$$=−\int_{\infty} ^{\:\mathrm{0}} {t}^{−\mathrm{2}} {f}\left(\left({t}−{t}^{−\mathrm{1}} \right)^{\mathrm{2}} \right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\:\infty} {t}^{−\mathrm{2}} {f}\left(\left({t}−{t}^{−\mathrm{1}} \right)^{\mathrm{2}} \right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\:\infty} {x}^{−\mathrm{2}} {f}\left(\left({x}−{x}^{−\mathrm{1}} \right)^{\mathrm{2}} \right){dx}\:\:\left({change}\:{variable}\:{x}={t}\right) \\ $$$${J}=\int_{\mathrm{0}} ^{\:\infty} {f}\left(\left({x}−{x}^{−\mathrm{1}} \right)^{\mathrm{2}} \right){dx}=\int_{\mathrm{0}} ^{\infty} {x}^{−\mathrm{2}} {f}\left(\left({x}−{x}^{−\mathrm{1}} \right)^{\mathrm{2}} \right){dx} \\ $$$$\mathrm{2}{J}=\int_{\mathrm{0}} ^{\:\infty} {f}\left(\left({x}−{x}^{−\mathrm{1}} \right)^{\mathrm{2}} \right){dx}+\int_{\mathrm{0}} ^{\infty} {x}^{−\mathrm{2}} {f}\left(\left({x}−{x}^{−\mathrm{1}} \right)^{\mathrm{2}} \right){dx} \\ $$$$\mathrm{2}{J}=\int_{\mathrm{0}} ^{\:\infty} \left(\mathrm{1}+{x}^{−\mathrm{2}} \right){f}\left(\left({x}−{x}^{−\mathrm{1}} \right)^{\mathrm{2}} \right){d} \\ $$$$\Rightarrow{J}=\mathrm{0}.\mathrm{5}\int_{\mathrm{0}} ^{\:\infty} \left(\mathrm{1}+{x}^{−\mathrm{2}} \right){f}\left(\left({x}−{x}^{−\mathrm{1}} \right)^{\mathrm{2}} \right){dx} \\ $$$${x}−{x}^{−\mathrm{1}} ={u}\Rightarrow\left(\mathrm{1}+{x}^{−\mathrm{2}} \right){dx}={du} \\ $$$${x}=\mathrm{0},{u}=−\infty \\ $$$${x}=\infty,{u}=\infty \\ $$$${J}=\mathrm{0}.\mathrm{5}\int_{\mathrm{0}} ^{\:\infty} \left(\mathrm{1}+{x}^{−\mathrm{2}} \right){f}\left(\left({x}−{x}^{−\mathrm{1}} \right)^{\mathrm{2}} \right){dx} \\ $$$$=\mathrm{0}.\mathrm{5}\int_{−\infty} ^{\infty} {f}\left({u}^{\mathrm{2}} \right){du} \\ $$$${f}\left({u}^{\mathrm{2}} \right)\:{is}\:{even},\:{hence} \\ $$$${J}=\mathrm{0}.\mathrm{5}×\mathrm{2}\int_{\mathrm{0}} ^{\infty} {f}\left({u}^{\mathrm{2}} \right){du}=\int_{\mathrm{0}} ^{\infty} {f}\left({u}^{\mathrm{2}} \right){du} \\ $$
Commented by Yozzi last updated on 07/Nov/15

$${Thanks}! \\ $$
