Menu Close

Let-lim-x-0-x-4-3-a-2-a-4-x-4-x-8-a-gt-0-If-is-finite-then-a-a-3-2-b-a-3-2-c-1-3-d-1-9-

Tinku Tara 0 Comments
Pin




Question Number 131789 by bemath last updated on 08/Feb/21
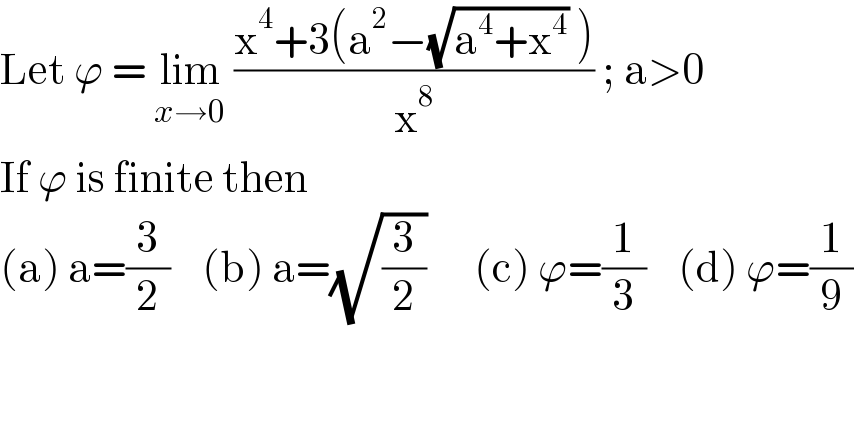
Let ϕ = lim_(x→0) ((x^4 +3(a^2 −(√(a^4 +x^4 )) ))/x^8 ) ; a>0 If ϕ is finite then (a) a=(3/2) (b) a=(√(3/2)) (c) ϕ=(1/3) (d) ϕ=(1/9)
$$\mathrm{Let}\:\varphi\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{3}\left(\mathrm{a}^{\mathrm{2}} −\sqrt{\mathrm{a}^{\mathrm{4}} +\mathrm{x}^{\mathrm{4}} }\:\right)}{\mathrm{x}^{\mathrm{8}} }\:;\:\mathrm{a}>\mathrm{0} \\ $$$$\mathrm{If}\:\varphi\:\mathrm{is}\:\mathrm{finite}\:\mathrm{then}\: \\ $$$$\left(\mathrm{a}\right)\:\mathrm{a}=\frac{\mathrm{3}}{\mathrm{2}}\:\:\:\:\left(\mathrm{b}\right)\:\mathrm{a}=\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\:\:\:\:\:\:\left(\mathrm{c}\right)\:\varphi=\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\:\left(\mathrm{d}\right)\:\varphi=\frac{\mathrm{1}}{\mathrm{9}} \\ $$
Answered by Dwaipayan Shikari last updated on 08/Feb/21
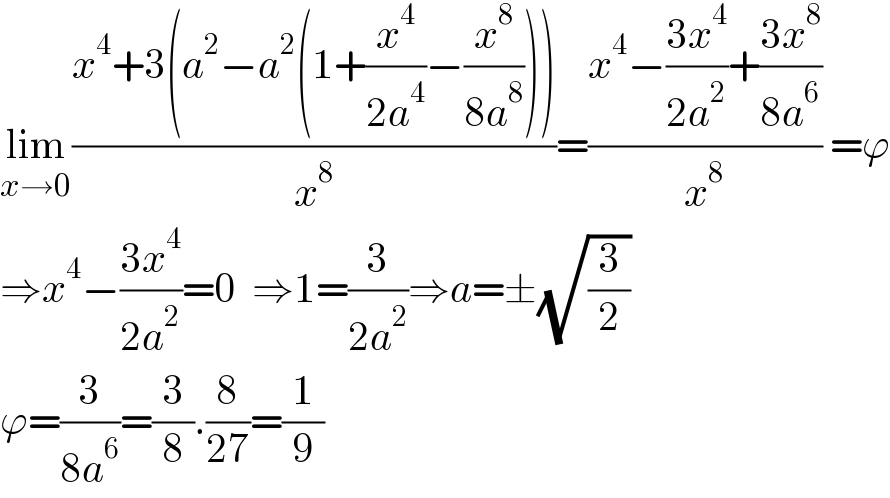
lim_(x→0) ((x^4 +3(a^2 −a^2 (1+(x^4 /(2a^4 ))−(x^8 /(8a^8 )))))/x^8 )=((x^4 −((3x^4 )/(2a^2 ))+((3x^8 )/(8a^6 )))/x^8 ) =ϕ ⇒x^4 −((3x^4 )/(2a^2 ))=0 ⇒1=(3/(2a^2 ))⇒a=±(√(3/2)) ϕ=(3/(8a^6 ))=(3/8).(8/(27))=(1/9)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{4}} +\mathrm{3}\left({a}^{\mathrm{2}} −{a}^{\mathrm{2}} \left(\mathrm{1}+\frac{{x}^{\mathrm{4}} }{\mathrm{2}{a}^{\mathrm{4}} }−\frac{{x}^{\mathrm{8}} }{\mathrm{8}{a}^{\mathrm{8}} }\right)\right)}{{x}^{\mathrm{8}} }=\frac{{x}^{\mathrm{4}} −\frac{\mathrm{3}{x}^{\mathrm{4}} }{\mathrm{2}{a}^{\mathrm{2}} }+\frac{\mathrm{3}{x}^{\mathrm{8}} }{\mathrm{8}{a}^{\mathrm{6}} }}{{x}^{\mathrm{8}} }\:=\varphi \\ $$$$\Rightarrow{x}^{\mathrm{4}} −\frac{\mathrm{3}{x}^{\mathrm{4}} }{\mathrm{2}{a}^{\mathrm{2}} }=\mathrm{0}\:\:\Rightarrow\mathrm{1}=\frac{\mathrm{3}}{\mathrm{2}{a}^{\mathrm{2}} }\Rightarrow{a}=\pm\sqrt{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\varphi=\frac{\mathrm{3}}{\mathrm{8}{a}^{\mathrm{6}} }=\frac{\mathrm{3}}{\mathrm{8}}.\frac{\mathrm{8}}{\mathrm{27}}=\frac{\mathrm{1}}{\mathrm{9}} \\ $$
Answered by EDWIN88 last updated on 08/Feb/21
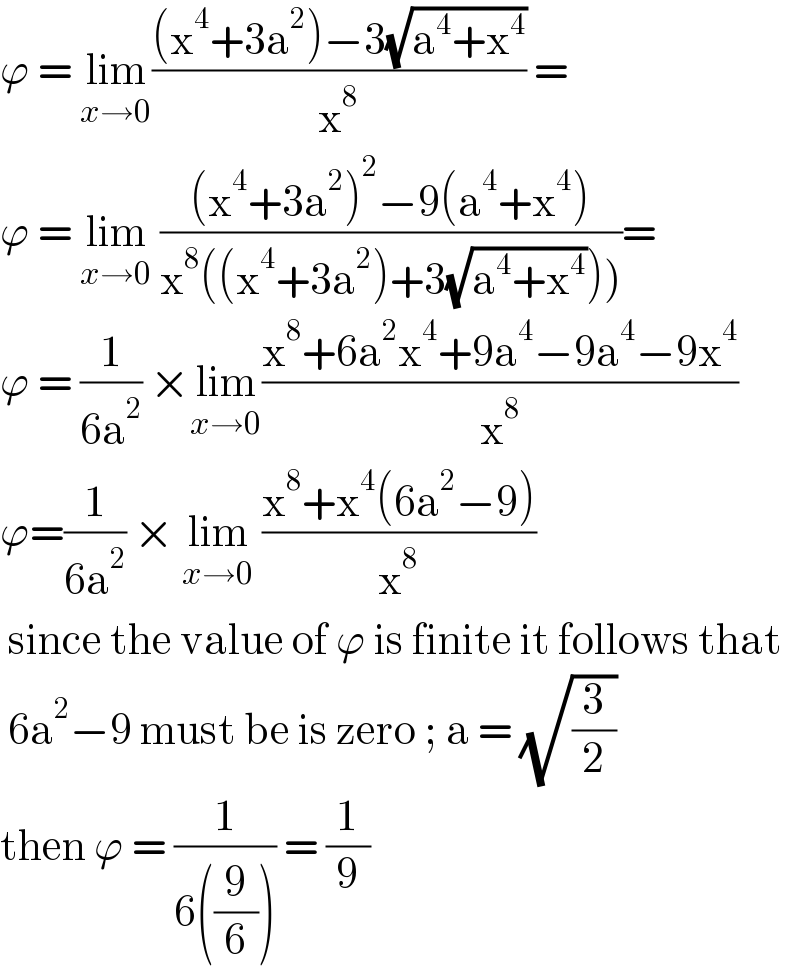
ϕ = lim_(x→0) (((x^4 +3a^2 )−3(√(a^4 +x^4 )))/x^8 ) = ϕ = lim_(x→0) (((x^4 +3a^2 )^2 −9(a^4 +x^4 ))/(x^8 ((x^4 +3a^2 )+3(√(a^4 +x^4 ))))))= ϕ = (1/(6a^2 )) ×lim_(x→0) ((x^8 +6a^2 x^4 +9a^4 −9a^4 −9x^4 )/x^8 ) ϕ=(1/(6a^2 )) × lim_(x→0) ((x^8 +x^4 (6a^2 −9))/x^8 ) since the value of ϕ is finite it follows that 6a^2 −9 must be is zero ; a = (√(3/2)) then ϕ = (1/(6((9/6)))) = (1/9)
$$\varphi\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{x}^{\mathrm{4}} +\mathrm{3a}^{\mathrm{2}} \right)−\mathrm{3}\sqrt{\mathrm{a}^{\mathrm{4}} +\mathrm{x}^{\mathrm{4}} }}{\mathrm{x}^{\mathrm{8}} }\:= \\ $$$$\varphi\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{x}^{\mathrm{4}} +\mathrm{3a}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{9}\left(\mathrm{a}^{\mathrm{4}} +\mathrm{x}^{\mathrm{4}} \right)}{\left.\mathrm{x}^{\mathrm{8}} \left(\left(\mathrm{x}^{\mathrm{4}} +\mathrm{3a}^{\mathrm{2}} \right)+\mathrm{3}\sqrt{\mathrm{a}^{\mathrm{4}} +\mathrm{x}^{\mathrm{4}} }\right)\right)}= \\ $$$$\varphi\:=\:\frac{\mathrm{1}}{\mathrm{6a}^{\mathrm{2}} }\:×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}^{\mathrm{8}} +\mathrm{6a}^{\mathrm{2}} \mathrm{x}^{\mathrm{4}} +\mathrm{9a}^{\mathrm{4}} −\mathrm{9a}^{\mathrm{4}} −\mathrm{9x}^{\mathrm{4}} }{\mathrm{x}^{\mathrm{8}} } \\ $$$$\varphi=\frac{\mathrm{1}}{\mathrm{6a}^{\mathrm{2}} }\:×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{8}} +\mathrm{x}^{\mathrm{4}} \left(\mathrm{6a}^{\mathrm{2}} −\mathrm{9}\right)}{\mathrm{x}^{\mathrm{8}} } \\ $$$$\:\mathrm{since}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\varphi\:\mathrm{is}\:\mathrm{finite}\:\mathrm{it}\:\mathrm{follows}\:\mathrm{that} \\ $$$$\:\mathrm{6a}^{\mathrm{2}} −\mathrm{9}\:\mathrm{must}\:\mathrm{be}\:\mathrm{is}\:\mathrm{zero}\:;\:\mathrm{a}\:=\:\sqrt{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\mathrm{then}\:\varphi\:=\:\frac{\mathrm{1}}{\mathrm{6}\left(\frac{\mathrm{9}}{\mathrm{6}}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{9}}\:\: \\ $$
Commented by liberty last updated on 08/Feb/21
Hallo Herr wie geht es dir
$$\mathrm{Hallo}\:\mathrm{Herr}\:\mathrm{wie}\:\mathrm{geht}\:\mathrm{es}\:\mathrm{dir}\: \\ $$
Commented by EDWIN88 last updated on 08/Feb/21
Hallo Herr auch. Gute Nachrichten
$$ \\ $$$$\mathrm{Hallo}\:\mathrm{Herr}\:\mathrm{auch}.\:\:\mathrm{Gute}\:\mathrm{Nachrichten} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *