Menu Close

let-n-0-2pi-cos-x-cos-2x-cos-nx-dx-for-which-integers-n-1-n-10-is-n-0-

Tinku Tara 0 Comments
Pin




Question Number 139474 by mathdanisur last updated on 27/Apr/21
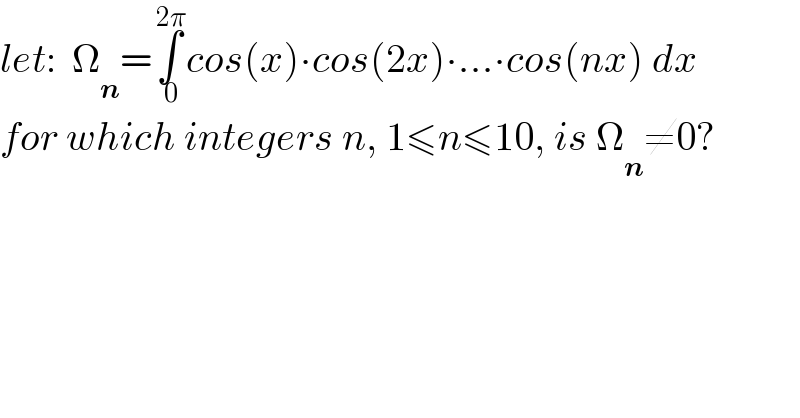
let: Ω_n =∫_( 0) ^( 2π) cos(x)∙cos(2x)∙...∙cos(nx) dx for which integers n, 1≤n≤10, is Ω_n ≠0?
$${let}:\:\:\Omega_{\boldsymbol{{n}}} =\underset{\:\mathrm{0}} {\overset{\:\mathrm{2}\pi} {\int}}{cos}\left({x}\right)\centerdot{cos}\left(\mathrm{2}{x}\right)\centerdot…\centerdot{cos}\left({nx}\right)\:{dx} \\ $$$${for}\:{which}\:{integers}\:{n},\:\mathrm{1}\leqslant{n}\leqslant\mathrm{10},\:{is}\:\Omega_{\boldsymbol{{n}}} \neq\mathrm{0}? \\ $$
Answered by mathmax by abdo last updated on 28/Apr/21
Φ_n =∫_0 ^π cosx.cos(2x)....cos(nx)dx +∫_π ^(2π) cosx cos(2x)....cos(nx)dx (→x=π+t) =∫_0 ^π cosx.cos(2x)...cos(nx)dx+∫_0 ^π cos(π+t).cos(π+2t)...cos(nπ+nt)dt =∫_0 ^π Π_(k=1) ^n cos(kx)dx +∫_0 ^π Π_(k=1) ^n cos(kπ +kx)dx =∫_0 ^π Π_(k=1) ^n cos(kx)dx+∫_0 ^π Π_(k=1) ^n (−1)^k cos(kx)dx =∫_0 ^π Π_(k=1) ^n cos(kx)dx +(−1)^((n(n+1))/2) ∫_0 ^π Π_(k=1) ^n cos(kx)dx =(1+(−1)^((n(n+1))/2) )∫_0 ^π Π_(k=1) ^n cos(kx)dx so Φ_n ≠0 ⇒ 1+(−1)^((n(n+1))/2) ≠0 and ∫_0 ^π cos(x).cos(2x)...cos(nx)dx ≠0 ....be continued...
$$\Phi_{\mathrm{n}} =\int_{\mathrm{0}} ^{\pi} \:\mathrm{cosx}.\mathrm{cos}\left(\mathrm{2x}\right)….\mathrm{cos}\left(\mathrm{nx}\right)\mathrm{dx}\:+\int_{\pi} ^{\mathrm{2}\pi} \:\mathrm{cosx}\:\mathrm{cos}\left(\mathrm{2x}\right)….\mathrm{cos}\left(\mathrm{nx}\right)\mathrm{dx} \\ $$$$\left(\rightarrow\mathrm{x}=\pi+\mathrm{t}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\mathrm{cosx}.\mathrm{cos}\left(\mathrm{2x}\right)…\mathrm{cos}\left(\mathrm{nx}\right)\mathrm{dx}+\int_{\mathrm{0}} ^{\pi} \mathrm{cos}\left(\pi+\mathrm{t}\right).\mathrm{cos}\left(\pi+\mathrm{2t}\right)…\mathrm{cos}\left(\mathrm{n}\pi+\mathrm{nt}\right)\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \:\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{cos}\left(\mathrm{kx}\right)\mathrm{dx}\:+\int_{\mathrm{0}} ^{\pi} \:\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{cos}\left(\mathrm{k}\pi\:+\mathrm{kx}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \:\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{cos}\left(\mathrm{kx}\right)\mathrm{dx}+\int_{\mathrm{0}} ^{\pi} \:\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{cos}\left(\mathrm{kx}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \:\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{cos}\left(\mathrm{kx}\right)\mathrm{dx}\:+\left(−\mathrm{1}\right)^{\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}} \:\int_{\mathrm{0}} ^{\pi} \:\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{cos}\left(\mathrm{kx}\right)\mathrm{dx} \\ $$$$=\left(\mathrm{1}+\left(−\mathrm{1}\right)^{\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}} \right)\int_{\mathrm{0}} ^{\pi} \:\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{cos}\left(\mathrm{kx}\right)\mathrm{dx}\:\mathrm{so}\:\Phi_{\mathrm{n}} \neq\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{1}+\left(−\mathrm{1}\right)^{\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}} \:\neq\mathrm{0}\:\mathrm{and}\:\int_{\mathrm{0}} ^{\pi} \mathrm{cos}\left(\mathrm{x}\right).\mathrm{cos}\left(\mathrm{2x}\right)…\mathrm{cos}\left(\mathrm{nx}\right)\mathrm{dx}\:\neq\mathrm{0} \\ $$$$….\mathrm{be}\:\mathrm{continued}… \\ $$
Commented by mathdanisur last updated on 30/Apr/21
thanks sir
$${thanks}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *