Question Number 1942 by Yozzi last updated on 25/Oct/15

$${Let}\:{N}\:{be}\:{a}\:{positive}\:{integer}\:{with}\:{prime} \\ $$$${factorisation}\: \\ $$$$\:\:{N}={p}_{\mathrm{1}} ^{{m}_{\mathrm{1}} } {p}_{\mathrm{2}} ^{{m}_{\mathrm{2}} } {p}_{\mathrm{3}} ^{{m}_{\mathrm{3}} } ×…×{p}_{{n}−\mathrm{1}} ^{{m}_{{n}−\mathrm{1}} } {p}_{{n}} ^{{m}_{{n}} } \\ $$$${where}\:\:{n},{m}_{{i}} \in\mathbb{Z}^{+} \:{and}\:{p}_{{r}} \:{is}\:{prime}. \\ $$$${How}\:{many}\:{proper}\:{factors}\:{does}\:{N}\:{have}? \\ $$$${Investigate}\:{cases}\:{where}\:{n}=\mathrm{1},{n}=\mathrm{2},\:{n}=\mathrm{3} \\ $$$${and}\:{n}=\mathrm{4}.\:{What}\:{is}\:{the}\:{smallest}\:{positive} \\ $$$${integer}\:{with}\:\mathrm{12}\:{proper}\:{factors}? \\ $$$${What}\:{is}\:{the}\:{smallest}\:{positive}\:{integer} \\ $$$${with}\:{at}\:{least}\:\mathrm{12}\:{proper}\:{factors}? \\ $$$$\left({A}\:{proper}\:{factor}\:{of}\:{a}\:{positive}\:{number}\:{N}\right. \\ $$$$\left.{is}\:{positive}\:{nteger}\:{M}\:{such}\:{that}\:{M}\neq\mathrm{1}\:{and}\:{M}\neq{N}.\right) \\ $$
Commented by prakash jain last updated on 25/Oct/15
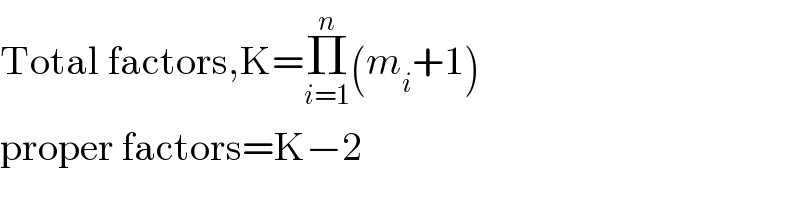
$$\mathrm{Total}\:\mathrm{factors},\mathrm{K}=\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}\left({m}_{{i}} +\mathrm{1}\right) \\ $$$$\mathrm{proper}\:\mathrm{factors}=\mathrm{K}−\mathrm{2} \\ $$
Answered by prakash jain last updated on 25/Oct/15
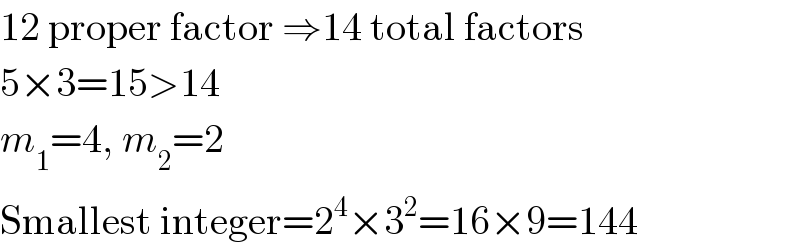
$$\mathrm{12}\:\mathrm{proper}\:\mathrm{factor}\:\Rightarrow\mathrm{14}\:\mathrm{total}\:\mathrm{factors} \\ $$$$\mathrm{5}×\mathrm{3}=\mathrm{15}>\mathrm{14} \\ $$$${m}_{\mathrm{1}} =\mathrm{4},\:{m}_{\mathrm{2}} =\mathrm{2} \\ $$$$\mathrm{Smallest}\:\mathrm{integer}=\mathrm{2}^{\mathrm{4}} ×\mathrm{3}^{\mathrm{2}} =\mathrm{16}×\mathrm{9}=\mathrm{144} \\ $$
