Menu Close

Let-n-be-the-smallest-positive-integer-that-is-a-multiple-of-75-and-has-exactly-75-positive-integral-divisors-including-1-and-itself-Find-n-75-

Tinku Tara 0 Comments
Pin




Question Number 11075 by Joel576 last updated on 10/Mar/17
Let n be the smallest positive integer that is a multiple of 75 and has exactly 75 positive integral divisors, including 1 and itself. Find (n/(75))
$$\mathrm{Let}\:{n}\:\mathrm{be}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{positive}\:\mathrm{integer}\:\mathrm{that}\:\mathrm{is} \\ $$$$\mathrm{a}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{75}\:\mathrm{and}\:\mathrm{has}\:\mathrm{exactly}\:\mathrm{75}\:\mathrm{positive} \\ $$$$\mathrm{integral}\:\mathrm{divisors},\:\mathrm{including}\:\mathrm{1}\:\mathrm{and}\:\mathrm{itself}. \\ $$$$\mathrm{Find}\:\frac{{n}}{\mathrm{75}} \\ $$
Commented by FilupS last updated on 11/Mar/17
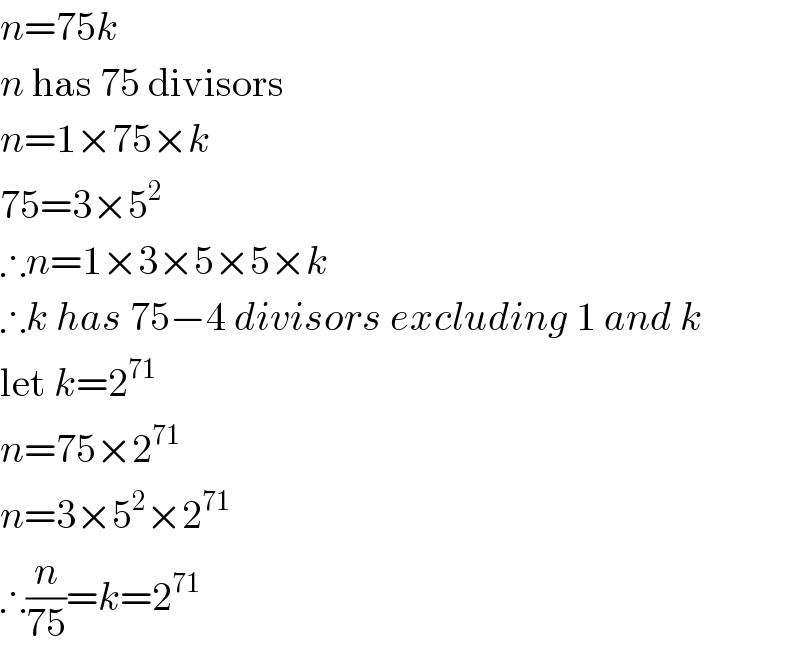
n=75k n has 75 divisors n=1×75×k 75=3×5^2 ∴n=1×3×5×5×k ∴k has 75−4 divisors excluding 1 and k let k=2^(71) n=75×2^(71) n=3×5^2 ×2^(71) ∴(n/(75))=k=2^(71)
$${n}=\mathrm{75}{k} \\ $$$${n}\:\mathrm{has}\:\mathrm{75}\:\mathrm{divisors} \\ $$$${n}=\mathrm{1}×\mathrm{75}×{k} \\ $$$$\mathrm{75}=\mathrm{3}×\mathrm{5}^{\mathrm{2}} \\ $$$$\therefore{n}=\mathrm{1}×\mathrm{3}×\mathrm{5}×\mathrm{5}×{k} \\ $$$$\therefore{k}\:{has}\:\mathrm{75}−\mathrm{4}\:{divisors}\:{excluding}\:\mathrm{1}\:{and}\:{k} \\ $$$$\mathrm{let}\:{k}=\mathrm{2}^{\mathrm{71}} \\ $$$${n}=\mathrm{75}×\mathrm{2}^{\mathrm{71}} \\ $$$${n}=\mathrm{3}×\mathrm{5}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{71}} \\ $$$$\therefore\frac{{n}}{\mathrm{75}}={k}=\mathrm{2}^{\mathrm{71}} \\ $$
Commented by mrW1 last updated on 14/Mar/17
The answer to this question depents very much on how to understand the condition “it has exactly 75 divisors”. Let′s look at an easier case that it has exactly 5 divisors. According to your consideration above the answer should be n=1×3×5×5×2^1 =150 But this number has not exactly only 5 divisors, but much more. All following numbers are divisors of it: 1/3/5/2 15/6 25/10 75/30/50 150 −−−−− that means the number n=150 has in fact not exactly 5 divisors, but exactly 12 different divisors. An orther problem is if identical divisors are allowed or not. Since 1 is definitely allowed, according to your consideration the answer should be n=1×3×5×5×1^(71) =75
$${The}\:{answer}\:{to}\:{this}\:{question}\:{depents} \\ $$$${very}\:{much}\:{on}\:{how}\:{to}\:{understand}\:{the} \\ $$$${condition}\:“{it}\:{has}\:{exactly}\:\mathrm{75}\:{divisors}''. \\ $$$$ \\ $$$${Let}'{s}\:{look}\:{at}\:{an}\:{easier}\:{case}\:{that}\:{it}\:{has} \\ $$$${exactly}\:\mathrm{5}\:{divisors}.\:{According}\:{to}\:{your} \\ $$$${consideration}\:{above}\:{the}\:{answer}\:{should} \\ $$$${be} \\ $$$${n}=\mathrm{1}×\mathrm{3}×\mathrm{5}×\mathrm{5}×\mathrm{2}^{\mathrm{1}} =\mathrm{150} \\ $$$${But}\:{this}\:{number}\:{has}\:{not}\:{exactly}\:{only} \\ $$$$\mathrm{5}\:{divisors},\:{but}\:{much}\:{more}.\:{All}\:{following} \\ $$$${numbers}\:{are}\:{divisors}\:{of}\:{it}: \\ $$$$\mathrm{1}/\mathrm{3}/\mathrm{5}/\mathrm{2} \\ $$$$\mathrm{15}/\mathrm{6} \\ $$$$\mathrm{25}/\mathrm{10} \\ $$$$\mathrm{75}/\mathrm{30}/\mathrm{50} \\ $$$$\mathrm{150} \\ $$$$−−−−− \\ $$$${that}\:{means}\:{the}\:{number}\:{n}=\mathrm{150}\:{has} \\ $$$${in}\:{fact}\:{not}\:{exactly}\:\mathrm{5}\:{divisors},\:{but} \\ $$$${exactly}\:\mathrm{12}\:{different}\:{divisors}. \\ $$$$ \\ $$$${An}\:{orther}\:{problem}\:{is}\:{if}\:{identical}\:{divisors} \\ $$$${are}\:{allowed}\:{or}\:{not}.\:{Since}\:\mathrm{1}\:{is}\:{definitely} \\ $$$${allowed},\:{according}\:{to}\:{your}\:{consideration} \\ $$$${the}\:{answer}\:{should}\:{be} \\ $$$${n}=\mathrm{1}×\mathrm{3}×\mathrm{5}×\mathrm{5}×\mathrm{1}^{\mathrm{71}} =\mathrm{75} \\ $$
Commented by FilupS last updated on 11/Mar/17
ahh. I was thinking of factors!
$${ahh}.\:\mathrm{I}\:\mathrm{was}\:\mathrm{thinking}\:\mathrm{of}\:\mathrm{factors}! \\ $$
Commented by mrW1 last updated on 11/Mar/17
I made following consideration: n=p_1 ×p_2 ×p_3 ....×p_m =Π_(k=1) ^m p_k p_k =the k−th prime number. n has following kinds of divisors: − each of the m prime numbers: C_1 ^m =((m!)/(1!(m−1)!))=m − product of every 2 of the m prime numbers: C_2 ^m =((m!)/(2!(m−2)!)) − product of every 3 of the m prime numbers: C_3 ^m =((m!)/(3!(m−3)!)) ...... − product of all of the m prime numbers: C_m ^m =((m!)/(m!(m−m)!))=1 that means the total number of divisors is Σ_(k=1) ^m C_k ^m =Σ_(k=1) ^m ((m!)/(k!(m−k)!))=2^m −1
$${I}\:{made}\:{following}\:{consideration}: \\ $$$${n}={p}_{\mathrm{1}} ×{p}_{\mathrm{2}} ×{p}_{\mathrm{3}} ….×{p}_{{m}} =\underset{{k}=\mathrm{1}} {\overset{{m}} {\prod}}{p}_{{k}} \\ $$$${p}_{{k}} ={the}\:{k}−{th}\:{prime}\:{number}. \\ $$$${n}\:{has}\:{following}\:{kinds}\:{of}\:{divisors}: \\ $$$$−\:{each}\:{of}\:{the}\:{m}\:{prime}\:{numbers}:\:{C}_{\mathrm{1}} ^{{m}} =\frac{{m}!}{\mathrm{1}!\left({m}−\mathrm{1}\right)!}={m} \\ $$$$−\:{product}\:{of}\:{every}\:\mathrm{2}\:{of}\:{the}\:{m}\:{prime}\:{numbers}:\:{C}_{\mathrm{2}} ^{{m}} \:=\frac{{m}!}{\mathrm{2}!\left({m}−\mathrm{2}\right)!} \\ $$$$−\:{product}\:{of}\:{every}\:\mathrm{3}\:{of}\:{the}\:{m}\:{prime}\:{numbers}:\:{C}_{\mathrm{3}} ^{{m}} \:=\frac{{m}!}{\mathrm{3}!\left({m}−\mathrm{3}\right)!} \\ $$$$…… \\ $$$$−\:{product}\:{of}\:{all}\:{of}\:{the}\:{m}\:{prime}\:{numbers}:\:{C}_{{m}} ^{{m}} \:=\frac{{m}!}{{m}!\left({m}−{m}\right)!}=\mathrm{1} \\ $$$$ \\ $$$${that}\:{means}\:{the}\:{total}\:{number}\:{of}\:{divisors}\:{is} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}{C}_{{k}} ^{{m}} =\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{{m}!}{{k}!\left({m}−{k}\right)!}=\mathrm{2}^{{m}} −\mathrm{1} \\ $$
Commented by FilupS last updated on 12/Mar/17
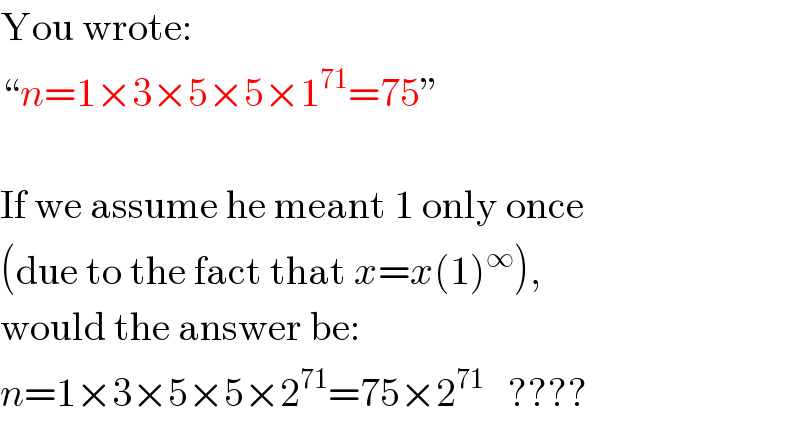
You wrote: “n=1×3×5×5×1^(71) =75” If we assume he meant 1 only once (due to the fact that x=x(1)^∞ ), would the answer be: n=1×3×5×5×2^(71) =75×2^(71) ????
$$\mathrm{You}\:\mathrm{wrote}: \\ $$$$“{n}=\mathrm{1}×\mathrm{3}×\mathrm{5}×\mathrm{5}×\mathrm{1}^{\mathrm{71}} =\mathrm{75}'' \\ $$$$\: \\ $$$$\mathrm{If}\:\mathrm{we}\:\mathrm{assume}\:\mathrm{he}\:\mathrm{meant}\:\mathrm{1}\:\mathrm{only}\:\mathrm{once} \\ $$$$\left(\mathrm{due}\:\mathrm{to}\:\mathrm{the}\:\mathrm{fact}\:\mathrm{that}\:{x}={x}\left(\mathrm{1}\right)^{\infty} \right), \\ $$$$\mathrm{would}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{be}: \\ $$$${n}=\mathrm{1}×\mathrm{3}×\mathrm{5}×\mathrm{5}×\mathrm{2}^{\mathrm{71}} =\mathrm{75}×\mathrm{2}^{\mathrm{71}} \:\:\:???? \\ $$
Commented by mrW1 last updated on 12/Mar/17
The difficulty lies on how to make the number to have exactly 75 divisors: − to get more divisors we should take more different prime numbers − to keep the number small we should use more 2′s. The general formula is n=2^n_1 ×3^n_2 ×5^n_3 ×7^n_4 ×11^n_5 ... with n_1 ,n_4 ,n_5 ,...≥0, n_2 ≥1,n_3 ≥2 The question is to determine n_1 ,n_2 ,n_3 ,... to keep n as small as possible and to have exactly 75 divisors. For example: n=2^(11) ×3×5^2 =153600 has 72 divisors n=2^(12) ×3×5^2 =307200 has 78 divisors n=2^3 ×3^2 ×5^2 ×7=12600 has 72 divisors n=2^4 ×3^2 ×5^2 ×7=25200 has 90 divisors n=2^2 ×3×5^2 ×7×11=23100 has 72 divisors n=2^3 ×3×5^2 ×7×11=46200 has 96 divisors We see it′s not the right way to use only factors 2. E.g. 2^(11) ×3×5^2 is much bigger than 2^3 ×3^2 ×5^2 ×7, but both have 72 divisors.
$${The}\:{difficulty}\:{lies}\:{on}\:{how}\:{to}\:{make} \\ $$$${the}\:{number}\:{to}\:{have}\:{exactly}\:\mathrm{75}\:{divisors}: \\ $$$$−\:{to}\:{get}\:{more}\:{divisors}\:{we}\:{should}\:{take} \\ $$$${more}\:{different}\:{prime}\:{numbers}\: \\ $$$$−\:{to}\:{keep}\:{the}\:{number}\:{small}\:{we}\:{should} \\ $$$${use}\:{more}\:\mathrm{2}'{s}. \\ $$$$ \\ $$$${The}\:{general}\:{formula}\:{is} \\ $$$${n}=\mathrm{2}^{{n}_{\mathrm{1}} } ×\mathrm{3}^{{n}_{\mathrm{2}} } ×\mathrm{5}^{{n}_{\mathrm{3}} } ×\mathrm{7}^{{n}_{\mathrm{4}} } ×\mathrm{11}^{{n}_{\mathrm{5}} } … \\ $$$${with}\:{n}_{\mathrm{1}} ,{n}_{\mathrm{4}} ,{n}_{\mathrm{5}} ,…\geqslant\mathrm{0},\:{n}_{\mathrm{2}} \geqslant\mathrm{1},{n}_{\mathrm{3}} \geqslant\mathrm{2} \\ $$$$ \\ $$$${The}\:{question}\:{is}\:{to}\:{determine} \\ $$$${n}_{\mathrm{1}} ,{n}_{\mathrm{2}} ,{n}_{\mathrm{3}} ,… \\ $$$${to}\:{keep}\:{n}\:{as}\:{small}\:{as}\:{possible}\:{and} \\ $$$${to}\:{have}\:{exactly}\:\mathrm{75}\:{divisors}. \\ $$$$ \\ $$$${For}\:{example}: \\ $$$${n}=\mathrm{2}^{\mathrm{11}} ×\mathrm{3}×\mathrm{5}^{\mathrm{2}} =\mathrm{153600}\:{has}\:\mathrm{72}\:{divisors} \\ $$$${n}=\mathrm{2}^{\mathrm{12}} ×\mathrm{3}×\mathrm{5}^{\mathrm{2}} =\mathrm{307200}\:{has}\:\mathrm{78}\:{divisors} \\ $$$$ \\ $$$${n}=\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{2}} ×\mathrm{5}^{\mathrm{2}} ×\mathrm{7}=\mathrm{12600}\:{has}\:\mathrm{72}\:{divisors} \\ $$$${n}=\mathrm{2}^{\mathrm{4}} ×\mathrm{3}^{\mathrm{2}} ×\mathrm{5}^{\mathrm{2}} ×\mathrm{7}=\mathrm{25200}\:{has}\:\mathrm{90}\:{divisors} \\ $$$$ \\ $$$${n}=\mathrm{2}^{\mathrm{2}} ×\mathrm{3}×\mathrm{5}^{\mathrm{2}} ×\mathrm{7}×\mathrm{11}=\mathrm{23100}\:{has}\:\mathrm{72}\:{divisors} \\ $$$${n}=\mathrm{2}^{\mathrm{3}} ×\mathrm{3}×\mathrm{5}^{\mathrm{2}} ×\mathrm{7}×\mathrm{11}=\mathrm{46200}\:{has}\:\mathrm{96}\:{divisors} \\ $$$$ \\ $$$${We}\:{see}\:{it}'{s}\:{not}\:{the}\:{right}\:{way}\:{to}\:{use} \\ $$$${only}\:{factors}\:\mathrm{2}.\:{E}.{g}.\:\mathrm{2}^{\mathrm{11}} ×\mathrm{3}×\mathrm{5}^{\mathrm{2}} \:{is}\:{much} \\ $$$${bigger}\:{than}\:\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{2}} ×\mathrm{5}^{\mathrm{2}} ×\mathrm{7},\:{but}\:{both} \\ $$$${have}\:\mathrm{72}\:{divisors}. \\ $$
Answered by mrW1 last updated on 16/Mar/17
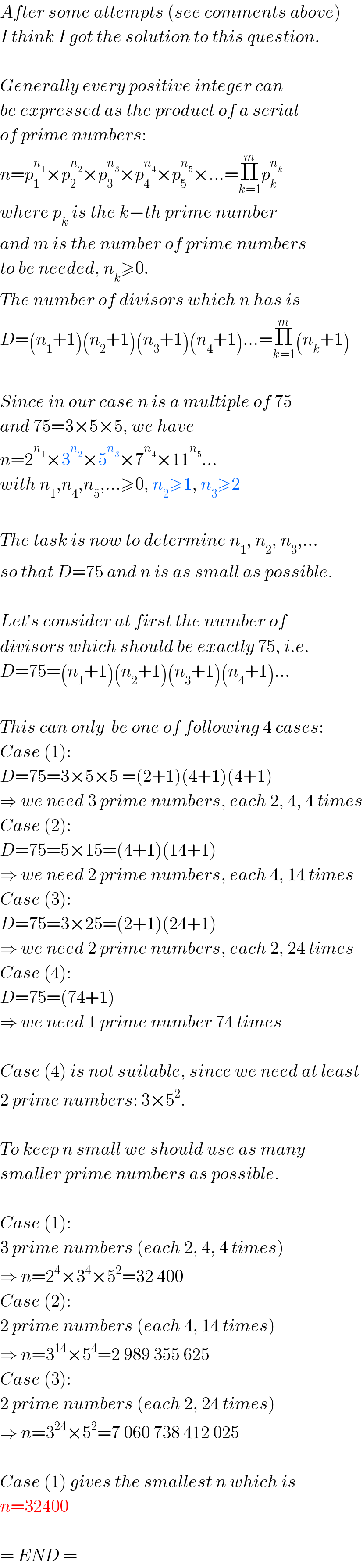
After some attempts (see comments above) I think I got the solution to this question. Generally every positive integer can be expressed as the product of a serial of prime numbers: n=p_1 ^n_1 ×p_2 ^n_2 ×p_3 ^n_3 ×p_4 ^n_4 ×p_5 ^n_5 ×...=Π_(k=1) ^m p_k ^n_k where p_k is the k−th prime number and m is the number of prime numbers to be needed, n_k ≥0. The number of divisors which n has is D=(n_1 +1)(n_2 +1)(n_3 +1)(n_4 +1)...=Π_(k=1) ^m (n_k +1) Since in our case n is a multiple of 75 and 75=3×5×5, we have n=2^n_1 ×3^n_2 ×5^n_3 ×7^n_4 ×11^n_5 ... with n_1 ,n_4 ,n_5 ,...≥0, n_2 ≥1, n_3 ≥2 The task is now to determine n_1 , n_2 , n_3 ,... so that D=75 and n is as small as possible. Let′s consider at first the number of divisors which should be exactly 75, i.e. D=75=(n_1 +1)(n_2 +1)(n_3 +1)(n_4 +1)... This can only be one of following 4 cases: Case (1): D=75=3×5×5 =(2+1)(4+1)(4+1) ⇒ we need 3 prime numbers, each 2, 4, 4 times Case (2): D=75=5×15=(4+1)(14+1) ⇒ we need 2 prime numbers, each 4, 14 times Case (3): D=75=3×25=(2+1)(24+1) ⇒ we need 2 prime numbers, each 2, 24 times Case (4): D=75=(74+1) ⇒ we need 1 prime number 74 times Case (4) is not suitable, since we need at least 2 prime numbers: 3×5^2 . To keep n small we should use as many smaller prime numbers as possible. Case (1): 3 prime numbers (each 2, 4, 4 times) ⇒ n=2^4 ×3^4 ×5^2 =32 400 Case (2): 2 prime numbers (each 4, 14 times) ⇒ n=3^(14) ×5^4 =2 989 355 625 Case (3): 2 prime numbers (each 2, 24 times) ⇒ n=3^(24) ×5^2 =7 060 738 412 025 Case (1) gives the smallest n which is n=32400 = END =
$${After}\:{some}\:{attempts}\:\left({see}\:{comments}\:{above}\right) \\ $$$${I}\:{think}\:{I}\:{got}\:{the}\:{solution}\:{to}\:{this}\:{question}. \\ $$$$ \\ $$$${Generally}\:{every}\:{positive}\:{integer}\:{can} \\ $$$${be}\:{expressed}\:{as}\:{the}\:{product}\:{of}\:{a}\:{serial} \\ $$$${of}\:{prime}\:{numbers}: \\ $$$${n}={p}_{\mathrm{1}} ^{{n}_{\mathrm{1}} } ×{p}_{\mathrm{2}} ^{{n}_{\mathrm{2}} } ×{p}_{\mathrm{3}} ^{{n}_{\mathrm{3}} } ×{p}_{\mathrm{4}} ^{{n}_{\mathrm{4}} } ×{p}_{\mathrm{5}} ^{{n}_{\mathrm{5}} } ×…=\underset{{k}=\mathrm{1}} {\overset{{m}} {\prod}}{p}_{{k}} ^{{n}_{{k}} } \\ $$$${where}\:{p}_{{k}} \:{is}\:{the}\:{k}−{th}\:{prime}\:{number} \\ $$$${and}\:{m}\:{is}\:{the}\:{number}\:{of}\:{prime}\:{numbers} \\ $$$${to}\:{be}\:{needed},\:{n}_{{k}} \geqslant\mathrm{0}. \\ $$$${The}\:{number}\:{of}\:{divisors}\:{which}\:{n}\:{has}\:{is} \\ $$$${D}=\left({n}_{\mathrm{1}} +\mathrm{1}\right)\left({n}_{\mathrm{2}} +\mathrm{1}\right)\left({n}_{\mathrm{3}} +\mathrm{1}\right)\left({n}_{\mathrm{4}} +\mathrm{1}\right)…=\underset{{k}=\mathrm{1}} {\overset{{m}} {\prod}}\left({n}_{{k}} +\mathrm{1}\right) \\ $$$$ \\ $$$${Since}\:{in}\:{our}\:{case}\:{n}\:{is}\:{a}\:{multiple}\:{of}\:\mathrm{75} \\ $$$${and}\:\mathrm{75}=\mathrm{3}×\mathrm{5}×\mathrm{5},\:{we}\:{have}\: \\ $$$${n}=\mathrm{2}^{{n}_{\mathrm{1}} } ×\mathrm{3}^{{n}_{\mathrm{2}} } ×\mathrm{5}^{{n}_{\mathrm{3}} } ×\mathrm{7}^{{n}_{\mathrm{4}} } ×\mathrm{11}^{{n}_{\mathrm{5}} } … \\ $$$${with}\:{n}_{\mathrm{1}} ,{n}_{\mathrm{4}} ,{n}_{\mathrm{5}} ,…\geqslant\mathrm{0},\:{n}_{\mathrm{2}} \geqslant\mathrm{1},\:{n}_{\mathrm{3}} \geqslant\mathrm{2} \\ $$$$ \\ $$$${The}\:{task}\:{is}\:{now}\:{to}\:{determine}\:{n}_{\mathrm{1}} ,\:{n}_{\mathrm{2}} ,\:{n}_{\mathrm{3}} ,… \\ $$$${so}\:{that}\:{D}=\mathrm{75}\:{and}\:{n}\:{is}\:{as}\:{small}\:{as}\:{possible}. \\ $$$$ \\ $$$${Let}'{s}\:{consider}\:{at}\:{first}\:{the}\:{number}\:{of} \\ $$$${divisors}\:{which}\:{should}\:{be}\:{exactly}\:\mathrm{75},\:{i}.{e}. \\ $$$${D}=\mathrm{75}=\left({n}_{\mathrm{1}} +\mathrm{1}\right)\left({n}_{\mathrm{2}} +\mathrm{1}\right)\left({n}_{\mathrm{3}} +\mathrm{1}\right)\left({n}_{\mathrm{4}} +\mathrm{1}\right)… \\ $$$$ \\ $$$${This}\:{can}\:{only}\:\:{be}\:{one}\:{of}\:{following}\:\mathrm{4}\:{cases}: \\ $$$${Case}\:\left(\mathrm{1}\right): \\ $$$${D}=\mathrm{75}=\mathrm{3}×\mathrm{5}×\mathrm{5}\:=\left(\mathrm{2}+\mathrm{1}\right)\left(\mathrm{4}+\mathrm{1}\right)\left(\mathrm{4}+\mathrm{1}\right) \\ $$$$\Rightarrow\:{we}\:{need}\:\mathrm{3}\:{prime}\:{numbers},\:{each}\:\mathrm{2},\:\mathrm{4},\:\mathrm{4}\:{times} \\ $$$${Case}\:\left(\mathrm{2}\right): \\ $$$${D}=\mathrm{75}=\mathrm{5}×\mathrm{15}=\left(\mathrm{4}+\mathrm{1}\right)\left(\mathrm{14}+\mathrm{1}\right)\: \\ $$$$\Rightarrow\:{we}\:{need}\:\mathrm{2}\:{prime}\:{numbers},\:{each}\:\mathrm{4},\:\mathrm{14}\:{times} \\ $$$${Case}\:\left(\mathrm{3}\right): \\ $$$${D}=\mathrm{75}=\mathrm{3}×\mathrm{25}=\left(\mathrm{2}+\mathrm{1}\right)\left(\mathrm{24}+\mathrm{1}\right)\: \\ $$$$\Rightarrow\:{we}\:{need}\:\mathrm{2}\:{prime}\:{numbers},\:{each}\:\mathrm{2},\:\mathrm{24}\:{times} \\ $$$${Case}\:\left(\mathrm{4}\right): \\ $$$${D}=\mathrm{75}=\left(\mathrm{74}+\mathrm{1}\right) \\ $$$$\Rightarrow\:{we}\:{need}\:\mathrm{1}\:{prime}\:{number}\:\mathrm{74}\:{times} \\ $$$$ \\ $$$${Case}\:\left(\mathrm{4}\right)\:{is}\:{not}\:{suitable},\:{since}\:{we}\:{need}\:{at}\:{least} \\ $$$$\mathrm{2}\:{prime}\:{numbers}:\:\mathrm{3}×\mathrm{5}^{\mathrm{2}} . \\ $$$$ \\ $$$${To}\:{keep}\:{n}\:{small}\:{we}\:{should}\:{use}\:{as}\:{many} \\ $$$${smaller}\:{prime}\:{numbers}\:{as}\:{possible}. \\ $$$$ \\ $$$${Case}\:\left(\mathrm{1}\right):\: \\ $$$$\mathrm{3}\:{prime}\:{numbers}\:\left({each}\:\mathrm{2},\:\mathrm{4},\:\mathrm{4}\:{times}\right) \\ $$$$\Rightarrow\:{n}=\mathrm{2}^{\mathrm{4}} ×\mathrm{3}^{\mathrm{4}} ×\mathrm{5}^{\mathrm{2}} =\mathrm{32}\:\mathrm{400} \\ $$$${Case}\:\left(\mathrm{2}\right):\: \\ $$$$\mathrm{2}\:{prime}\:{numbers}\:\left({each}\:\mathrm{4},\:\mathrm{14}\:{times}\right) \\ $$$$\Rightarrow\:{n}=\mathrm{3}^{\mathrm{14}} ×\mathrm{5}^{\mathrm{4}} =\mathrm{2}\:\mathrm{989}\:\mathrm{355}\:\mathrm{625} \\ $$$${Case}\:\left(\mathrm{3}\right):\: \\ $$$$\mathrm{2}\:{prime}\:{numbers}\:\left({each}\:\mathrm{2},\:\mathrm{24}\:{times}\right) \\ $$$$\Rightarrow\:{n}=\mathrm{3}^{\mathrm{24}} ×\mathrm{5}^{\mathrm{2}} =\mathrm{7}\:\mathrm{060}\:\mathrm{738}\:\mathrm{412}\:\mathrm{025} \\ $$$$ \\ $$$${Case}\:\left(\mathrm{1}\right)\:{gives}\:{the}\:{smallest}\:{n}\:{which}\:{is} \\ $$$${n}=\mathrm{32400} \\ $$$$ \\ $$$$=\:{END}\:= \\ $$
Commented by Joel576 last updated on 13/Mar/17
Hi, mrW1 Thank you very much for your great solution Even my teacher, he haven′t found any solutions yet. Glad you wanted to spend your time to find the solution.
$${Hi},\:\mathrm{mrW1} \\ $$$${Thank}\:{you}\:{very}\:{much}\:{for}\:{your}\:{great}\:{solution} \\ $$$${Even}\:{my}\:{teacher},\:{he}\:{haven}'{t}\:{found}\:{any}\:{solutions}\:{yet}. \\ $$$${Glad}\:{you}\:{wanted}\:{to}\:{spend}\:{your}\:{time}\:{to}\:{find}\:{the}\:{solution}. \\ $$
Commented by FilupS last updated on 13/Mar/17
I think mrW1 is the smartest person on here in the widest range of maths. Do you goto collage/university? I am completely self study. Math is my hobby.
$$\mathrm{I}\:\mathrm{think}\:\mathrm{mrW1}\:\mathrm{is}\:\mathrm{the}\:\mathrm{smartest}\:\mathrm{person}\:\mathrm{on} \\ $$$$\mathrm{here}\:\mathrm{in}\:\mathrm{the}\:\mathrm{widest}\:\mathrm{range}\:\mathrm{of}\:\mathrm{maths}.\:\mathrm{Do}\:\mathrm{you} \\ $$$$\mathrm{goto}\:\mathrm{collage}/\mathrm{university}?\:\mathrm{I}\:\mathrm{am}\:\mathrm{completely} \\ $$$$\mathrm{self}\:\mathrm{study}.\:\mathrm{Math}\:\mathrm{is}\:\mathrm{my}\:\mathrm{hobby}. \\ $$
Commented by FilupS last updated on 13/Mar/17
My strongest topic is in sequences and in number theory. I want to learn linear algebra
$$\mathrm{My}\:\mathrm{strongest}\:\mathrm{topic}\:\mathrm{is}\:\mathrm{in}\:\mathrm{sequences}\:\mathrm{and}\:\mathrm{in} \\ $$$$\mathrm{number}\:\mathrm{theory}.\:\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{learn}\:\mathrm{linear} \\ $$$$\mathrm{algebra} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *