let-set-S-R-let-nS-R-R-R-n-sets-of-R-n-Z-is-S-lt-nS-what-if-n-S-

Question Number 11145 by FilupS last updated on 14/Mar/17

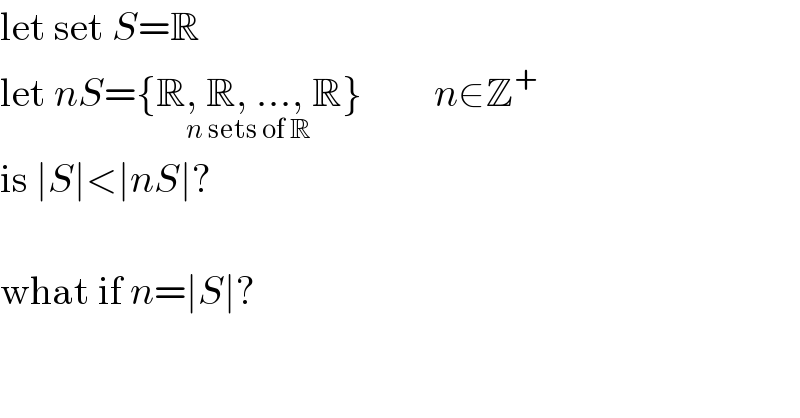
let set S=R let nS={R, R, ..., R_(n sets of R) } n∈Z^+ is ∣S∣<∣nS∣? what if n=∣S∣?

$$\mathrm{let}\:\mathrm{set}\:{S}=\mathbb{R} \\ $$$$\mathrm{let}\:{nS}=\left\{\underset{{n}\:\mathrm{sets}\:\mathrm{of}\:\mathbb{R}} {\mathbb{R},\:\mathbb{R},\:…,\:\mathbb{R}}\right\}\:\:\:\:\:\:\:\:\:{n}\in\mathbb{Z}^{+} \\ $$$$\mathrm{is}\:\mid{S}\mid<\mid{nS}\mid? \\ $$$$\: \\ $$$$\mathrm{what}\:\mathrm{if}\:{n}=\mid{S}\mid? \\ $$

Commented by prakash jain last updated on 15/Mar/17

S is noy countable. ∣nS∣=1 since duplicate elements are removed. nS is a set of sets.

$$\mathrm{S}\:\mathrm{is}\:\mathrm{noy}\:\mathrm{countable}. \\ $$$$\mid{nS}\mid=\mathrm{1}\:\mathrm{since}\:\mathrm{duplicate}\:\mathrm{elements}\:\mathrm{are}\:\mathrm{removed}. \\ $$$${n}\mathrm{S}\:{is}\:{a}\:{set}\:{of}\:{sets}. \\ $$

Facebook Tweet Pin

let-set-S-R-let-nS-R-R-R-n-sets-of-R-n-Z-is-S-lt-nS-what-if-n-S-

Leave a Reply Cancel reply