Question Number 67236 by prof Abdo imad last updated on 24/Aug/19
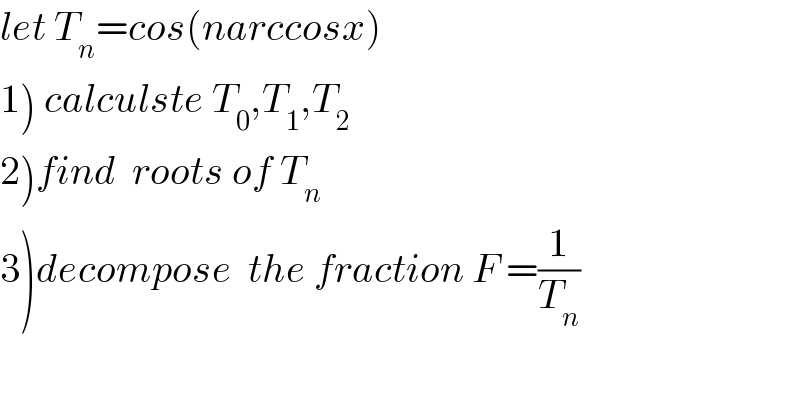
$${let}\:{T}_{{n}} ={cos}\left({narccosx}\right) \\ $$$$\left.\mathrm{1}\right)\:{calculste}\:{T}_{\mathrm{0}} ,{T}_{\mathrm{1}} ,{T}_{\mathrm{2}} \\ $$$$\left.\mathrm{2}\right){find}\:\:{roots}\:{of}\:{T}_{{n}} \\ $$$$\left.\mathrm{3}\right){decompose}\:\:{the}\:{fraction}\:{F}\:=\frac{\mathrm{1}}{{T}_{{n}} } \\ $$
Commented by mathmax by abdo last updated on 25/Aug/19
![1) T_0 =cos(0)=1 T_1 (x) =cos(arcosx)=x T_2 (x) =cos(2 arcosx) =2x^2 −1 wecan prove that T_n is a polynom with degT_n =n 2) T_n (x)=0 ⇔cos(narcosx)=0 ⇔narcosx =(π/2)+kπ k∈Z ⇔ arccosx =(π/(2n)) +((kπ)/n) ⇒ x_k =cos((π/(2n)) +((kπ)/n)) with k∈[[0,n−1]] 3) we have T_n (x) =a Π_(k=0) ^(n−1) (x−x_k ) with a is thedominent coefficient of T_n ⇒(1/(T_n (x))) =(1/(aΠ_(k=0) ^(n−1) (x−x_k ))) =Σ_(k=0) ^(n−1) (λ_k /(x−x_k )) and λ_k =(1/(T^′ (x_k ))) we have T^′ (x) =a Σ_(k=0) ^(n−1) Π_(j_(j≠k) =0) ^(n−1) (x−x_j ) ⇒ T^′ (x_k ) =a Σ_(k=0) ^(n−1) Π_(j=0_(j≠k) ) ^(n−1) (x_k −x_j )](https://www.tinkutara.com/question/Q67324.png)
$$\left.\mathrm{1}\right)\:{T}_{\mathrm{0}} ={cos}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${T}_{\mathrm{1}} \left({x}\right)\:={cos}\left({arcosx}\right)={x} \\ $$$${T}_{\mathrm{2}} \left({x}\right)\:={cos}\left(\mathrm{2}\:{arcosx}\right)\:=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}\:\:\:{wecan}\:{prove}\:{that}\:{T}_{{n}} {is}\:{a}\:{polynom} \\ $$$${with}\:{degT}_{{n}} ={n} \\ $$$$\left.\mathrm{2}\right)\:{T}_{{n}} \left({x}\right)=\mathrm{0}\:\Leftrightarrow{cos}\left({narcosx}\right)=\mathrm{0}\:\Leftrightarrow{narcosx}\:=\frac{\pi}{\mathrm{2}}+{k}\pi\:\:{k}\in{Z}\:\Leftrightarrow \\ $$$${arccosx}\:=\frac{\pi}{\mathrm{2}{n}}\:+\frac{{k}\pi}{{n}}\:\Rightarrow\:{x}_{{k}} ={cos}\left(\frac{\pi}{\mathrm{2}{n}}\:+\frac{{k}\pi}{{n}}\right)\:\:{with}\:{k}\in\left[\left[\mathrm{0},{n}−\mathrm{1}\right]\right] \\ $$$$\left.\mathrm{3}\right)\:{we}\:{have}\:{T}_{{n}} \left({x}\right)\:={a}\:\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}−{x}_{{k}} \right)\:\:\:{with}\:{a}\:{is}\:{thedominent} \\ $$$${coefficient}\:{of}\:{T}_{{n}} \:\Rightarrow\frac{\mathrm{1}}{{T}_{{n}} \left({x}\right)}\:=\frac{\mathrm{1}}{{a}\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}−{x}_{{k}} \right)} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{\lambda_{{k}} }{{x}−{x}_{{k}} }\:\:\:\:{and}\:\:\lambda_{{k}} =\frac{\mathrm{1}}{{T}\:^{'} \left({x}_{{k}} \right)}\:\:\:{we}\:{have}\: \\ $$$${T}\:^{'} \left({x}\right)\:={a}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\prod_{{j}_{{j}\neq{k}} =\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}−{x}_{{j}} \right)\:\Rightarrow \\ $$$${T}\:^{'} \left({x}_{{k}} \right)\:={a}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\prod_{{j}=\mathrm{0}_{{j}\neq{k}} } ^{{n}−\mathrm{1}} \:\:\:\left({x}_{{k}} −{x}_{{j}} \right) \\ $$
Answered by mind is power last updated on 24/Aug/19

$${T}_{\mathrm{0}} ={cos}\left(\mathrm{0}\right)=\mathrm{1}\:{T}_{\mathrm{1}} ={cos}\left({arcos}\left({x}\right)\right)={x} \\ $$$${T}_{\mathrm{2}} ={cos}\left(\mathrm{2}{arcos}\left({x}\right)\right)=\mathrm{2}{cos}^{\mathrm{2}} \left({arcos}\left({x}\right)\right)−\mathrm{1}=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1} \\ $$$${T}_{{n}} =\mathrm{0}\Rightarrow{cos}\left({narcos}\left({x}\right)\right)=\mathrm{0}\Rightarrow{n}\:{arcos}\left({x}\right)=\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi\:{withe}\: \\ $$$${arcos}\left({x}\right)=\left\{\frac{\mathrm{1}}{\mathrm{2}{n}}+\frac{\mathrm{2}{k}}{{n}}\right\}\pi \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}{n}}+\frac{\mathrm{2}{k}}{{n}}\leqslant\mathrm{1}\Rightarrow\mathrm{1}+\mathrm{4}{k}\leqslant\mathrm{2}{n}\Rightarrow{k}\leqslant\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{4}} \\ $$$${k}\in\left\{\mathrm{0},\mathrm{1},\:\:\:\:\:{E}\left(\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{4}}\right)\right\} \\ $$$${or}\:{narcos}\left({x}\right)=−\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi\Rightarrow\left(−\frac{\mathrm{1}}{\mathrm{2}{n}}+\frac{\mathrm{2}{k}}{{n}}\right)\pi\leqslant\pi \\ $$$$\Rightarrow\mathrm{4}{k}\leqslant\mathrm{2}{n}+\mathrm{1}\Rightarrow{k}\leqslant\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{4}} \\ $$$${solution}\:{ar}\:{cos}\left(\frac{\mathrm{1}+\mathrm{4}{k}}{\mathrm{2}{n}}\pi\right){withe}\:{k}\leqslant{E}\left(\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{4}}\right).{and}\:{cos}\left(\frac{\mathrm{4}{k}−\mathrm{1}}{\mathrm{2}{n}}\pi\right).{k}\leqslant{E}\left(\frac{\mathrm{2}{n}+\mathrm{1}{u}}{\mathrm{4}}\right) \\ $$$${Tn}=\underset{{k}=\mathrm{0}} {\overset{{E}\left(\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{4}}\right)} {\coprod}}\left({x}−{cos}\left(\frac{\mathrm{1}+\mathrm{4}{k}}{\mathrm{2}{n}}\pi\right)\right)\underset{{k}=\mathrm{0}} {\overset{{E}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{4}}\right)} {\prod}}\left({x}−{cos}\left(\frac{\mathrm{4}{k}−\mathrm{1}}{\mathrm{2}{n}}\pi\right)\right) \\ $$$$\frac{\mathrm{1}}{{Tn}}=\underset{{k}=\mathrm{0}} {\overset{{E}\left(\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{4}}\right)} {\sum}}\frac{{a}_{{k}} }{\left({x}−{cos}\left(\frac{\mathrm{1}+\mathrm{4}{k}}{\mathrm{2}{n}}\pi\right)\right)}+\underset{{k}=\mathrm{0}} {\overset{{E}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{4}}\right)} {\sum}}\frac{{a}_{{k}} }{\left({x}−{cos}\left(\frac{\mathrm{4}{k}−\mathrm{1}}{\mathrm{2}{n}}\pi\right)\right.} \\ $$$${a}_{{k}} =\underset{{j}=\mathrm{0}.{j}\neq{k}} {\overset{{E}\left(\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{4}}\right)} {\coprod}}\left({x}−{cos}\left(\frac{\mathrm{1}+\mathrm{4}{j}}{\mathrm{2}{n}}\pi\right)\right)\underset{{j}=\mathrm{0}.{j}#{k}} {\overset{{E}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{4}}\right)} {\prod}}\left({x}−{cos}\left(\frac{\mathrm{4}{j}−\mathrm{1}}{\mathrm{2}{n}}\pi\right)\right) \\ $$$$ \\ $$$$ \\ $$
Commented by Kunal12588 last updated on 24/Aug/19
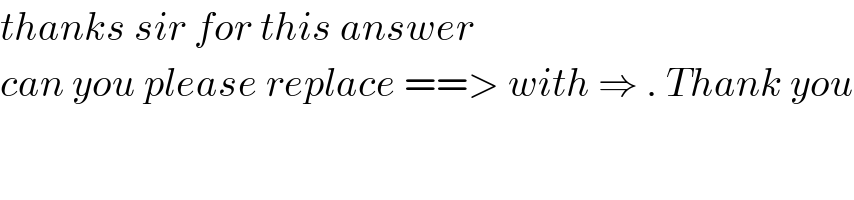
$${thanks}\:{sir}\:{for}\:{this}\:{answer} \\ $$$${can}\:{you}\:{please}\:{replace}\:==>\:{with}\:\Rightarrow\:.\:{Thank}\:{you} \\ $$
Commented by mind is power last updated on 24/Aug/19
$${ok}\:{wothe}\:{pleasur} \\ $$$$ \\ $$
