Question Number 4250 by Yozzii last updated on 06/Jan/16

$${Let}\:{u}=\frac{{ln}\left(\mathrm{3}−\left\{\frac{{ln}\left(\mathrm{3}−\left[\frac{{ln}\left(\mathrm{3}−\left(\ldots\right.\right.}{{ln}\left(\mathrm{2}+\left(\ldots\right.\right.}\right.\right.}{{ln}\left(\mathrm{2}+\left[\frac{{ln}\left(\mathrm{3}−\left(\ldots\right.\right.}{{ln}\left(\mathrm{2}+\left(\ldots\right.\right.}\right.\right.}\right\}\right)}{{ln}\left(\mathrm{2}+\left\{\frac{{ln}\left(\mathrm{3}−\left[\frac{{ln}\left(\mathrm{3}−\left(\ldots\right.\right.}{{ln}\left(\mathrm{2}+\left(\ldots\right.\right.}\right.\right.}{{ln}\left(\mathrm{2}+\left[\frac{{ln}\left(\mathrm{3}−\left(\ldots\right.\right.}{{ln}\left(\mathrm{2}+\left(\ldots\right.\right.}\right.\right.}\right\}\right)}. \\ $$$${What}\:{is}\:{the}\:{value}\:{of}\:{u}?\: \\ $$$$ \\ $$$${Let}\:{k}=\frac{{ln}\left({x}−\left\{\frac{{ln}\left({x}−\left[\frac{{ln}\left({x}−\left(\ldots\right.\right.}{{ln}\left({x}−\mathrm{1}+\left(\ldots\right.\right.}\right.\right.}{{ln}\left({x}−\mathrm{1}+\left[\frac{{ln}\left({x}−\left(\ldots\right.\right.}{{ln}\left({x}−\mathrm{1}+\left(\ldots\right.\right.}\right.\right.}\right\}\right)}{{ln}\left({x}−\mathrm{1}+\left\{\frac{{ln}\left({x}−\left[\frac{{ln}\left({x}−\left(\ldots\right.\right.}{{ln}\left({x}−\mathrm{1}+\left(\ldots\right.\right.}\right.\right.}{{ln}\left({x}−\mathrm{1}+\left[\frac{{ln}\left({x}−\left(\ldots\right.\right.}{{ln}\left({x}−\mathrm{1}+\left(\ldots\right.\right.}\right.\right.}\right\}\right)}. \\ $$$${For}\:{what}\:{values}\:{of}\:{x}\:{does} \\ $$$$\left({i}\right)\:{k}\:{converge}\:\left({ii}\right)\:{k}\:{diverge}? \\ $$
Commented by Yozzii last updated on 06/Jan/16
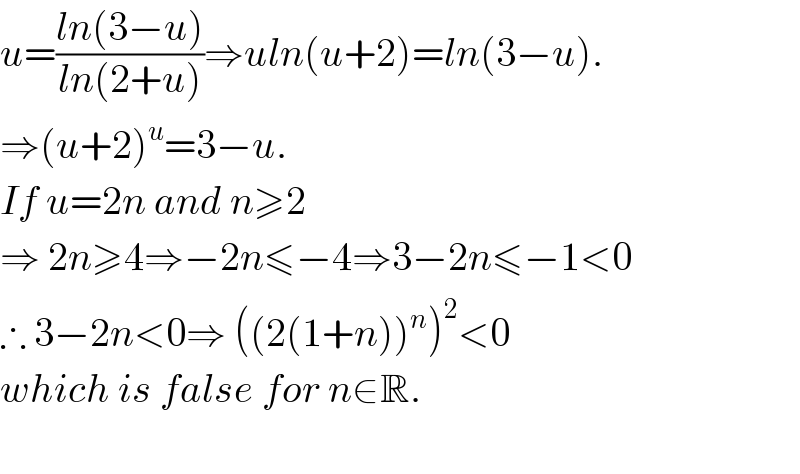
$${u}=\frac{{ln}\left(\mathrm{3}−{u}\right)}{{ln}\left(\mathrm{2}+{u}\right)}\Rightarrow{uln}\left({u}+\mathrm{2}\right)={ln}\left(\mathrm{3}−{u}\right). \\ $$$$\Rightarrow\left({u}+\mathrm{2}\right)^{{u}} =\mathrm{3}−{u}. \\ $$$${If}\:{u}=\mathrm{2}{n}\:{and}\:{n}\geqslant\mathrm{2} \\ $$$$\Rightarrow\:\mathrm{2}{n}\geqslant\mathrm{4}\Rightarrow−\mathrm{2}{n}\leqslant−\mathrm{4}\Rightarrow\mathrm{3}−\mathrm{2}{n}\leqslant−\mathrm{1}<\mathrm{0} \\ $$$$\therefore\:\mathrm{3}−\mathrm{2}{n}<\mathrm{0}\Rightarrow\:\left(\left(\mathrm{2}\left(\mathrm{1}+{n}\right)\right)^{{n}} \right)^{\mathrm{2}} <\mathrm{0}\: \\ $$$${which}\:{is}\:{false}\:{for}\:{n}\in\mathbb{R}.\: \\ $$$$ \\ $$
Commented by prakash jain last updated on 06/Jan/16

$${u}=\mathrm{1} \\ $$$$\mathrm{LHS}=\mathrm{3},\:\mathrm{RHS}=\mathrm{2},\:\mathrm{LHS}>\mathrm{RHS} \\ $$$${u}=\mathrm{0}.\mathrm{5} \\ $$$$\mathrm{LHS}=\sqrt{\frac{\mathrm{5}}{\mathrm{2}}}\:,\:\mathrm{RHS}=\mathrm{2}.\mathrm{5},\:\mathrm{LHS}<\mathrm{RHS} \\ $$$$\mathrm{some}\:\mathrm{solution}\:\mathrm{may}\:\mathrm{be}\:\mathrm{there}\:\mathrm{between}\:\mathrm{0}.\mathrm{5}\:\mathrm{and}\:\mathrm{1}. \\ $$
Commented by Yozzii last updated on 07/Jan/16
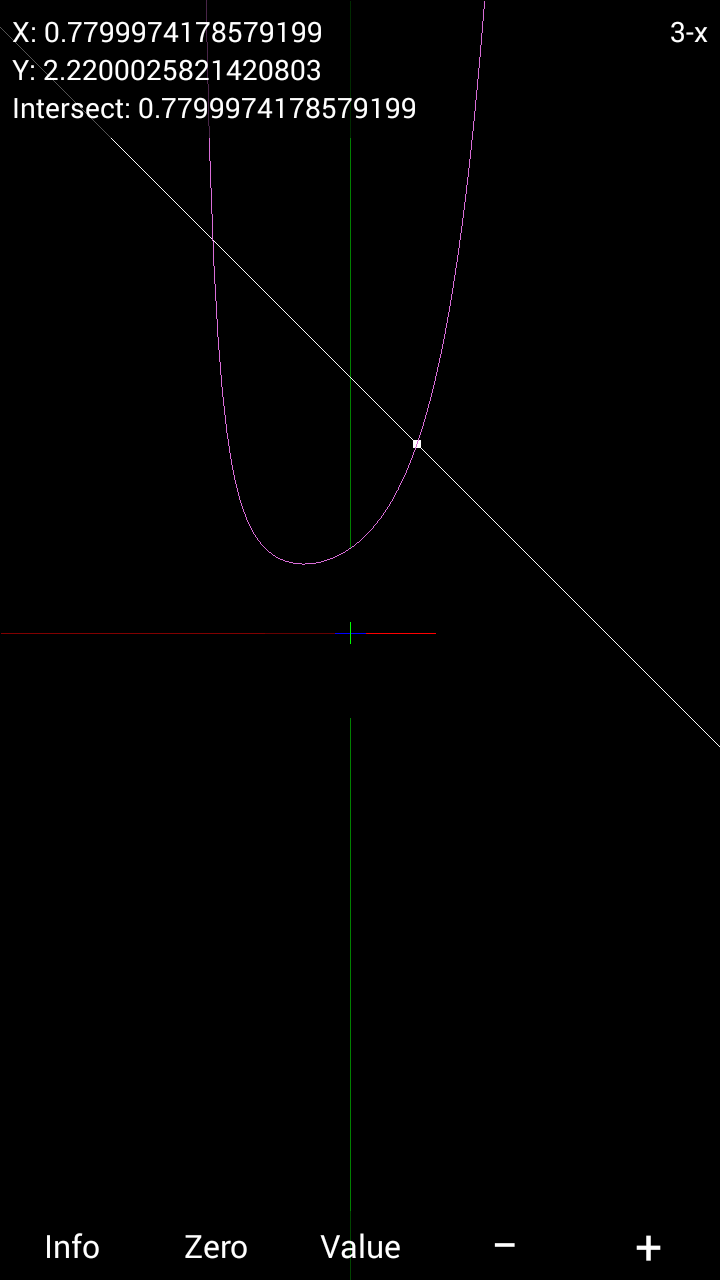
Commented by Yozzii last updated on 07/Jan/16
$${This}\:{indicates}\:{the}\:{positive}\:{root}\:{u} \\ $$$${of}\:{the}\:{equation}\:{being}\:{about}\:\mathrm{0}.\mathrm{78} \\ $$
Commented by Yozzii last updated on 07/Jan/16
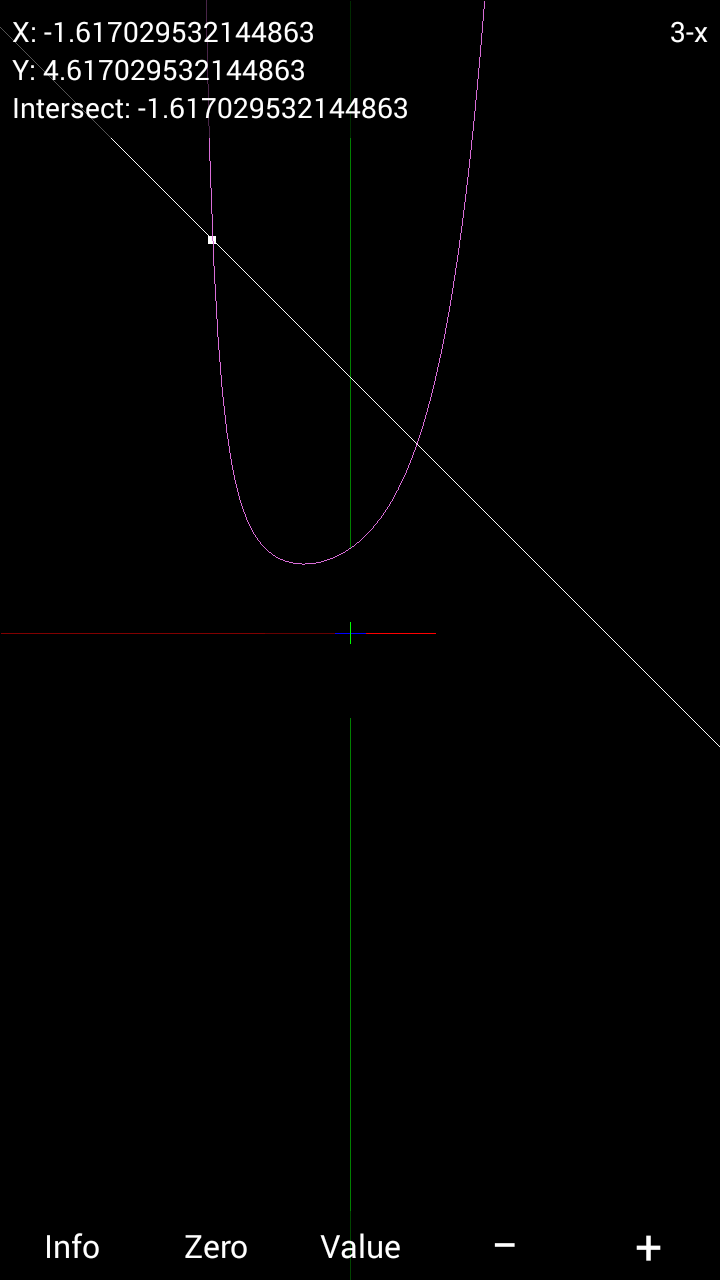
Commented by Yozzii last updated on 07/Jan/16

$${However},\:{the}\:{second}\:{root}\:{u}\:{is} \\ $$$${shown}\:{to}\:{be}\:{about}\:−\mathrm{1}.\mathrm{62}.\:{Is}\:{there}\:{a} \\ $$$${proof}\:{that}\:{would}\:{indicate}\:{the}\:{true} \\ $$$${sign}\:{or}\:{u},\:{if}\:{it}\:{is}\:{it}\:{can}\:{only}\:{take}\:{one}? \\ $$
