Question Number 133121 by abdomsup last updated on 19/Feb/21
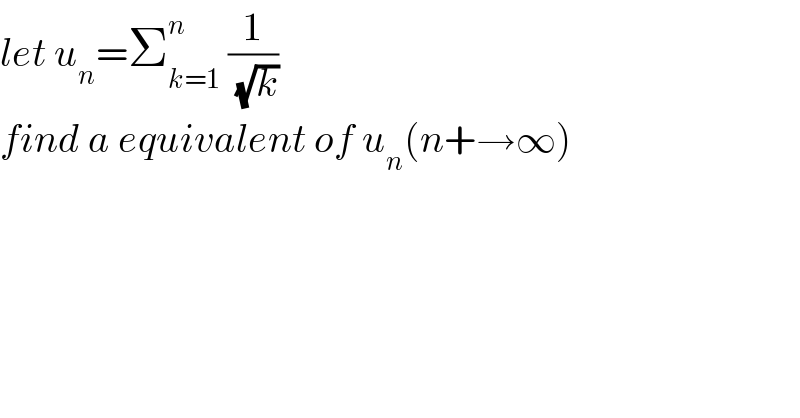
$${let}\:{u}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\:\sqrt{{k}}} \\ $$$${find}\:{a}\:{equivalent}\:{of}\:{u}_{{n}} \left({n}+\rightarrow\infty\right) \\ $$
Answered by mindispower last updated on 19/Feb/21
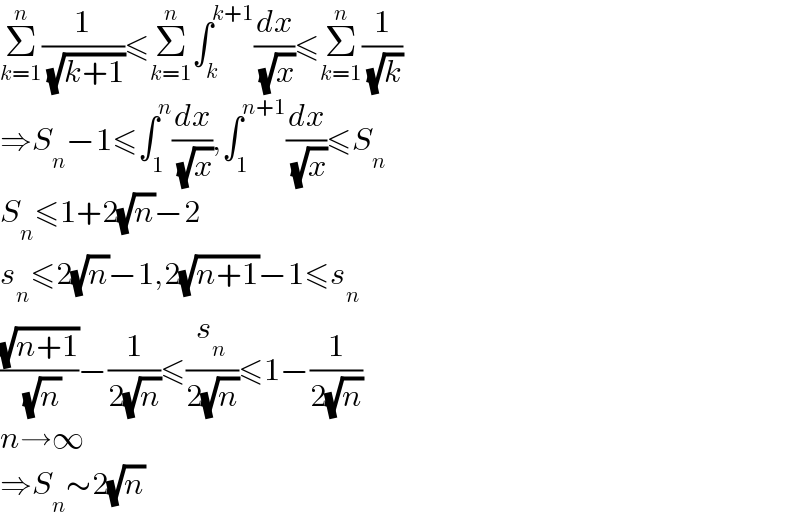
$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{k}+\mathrm{1}}}\leqslant\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\int_{{k}} ^{{k}+\mathrm{1}} \frac{{dx}}{\:\sqrt{{x}}}\leqslant\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{k}}} \\ $$$$\Rightarrow{S}_{{n}} −\mathrm{1}\leqslant\int_{\mathrm{1}} ^{{n}} \frac{{dx}}{\:\sqrt{{x}}},\int_{\mathrm{1}} ^{{n}+\mathrm{1}} \frac{{dx}}{\:\sqrt{{x}}}\leqslant{S}_{{n}} \\ $$$${S}_{{n}} \leqslant\mathrm{1}+\mathrm{2}\sqrt{{n}}−\mathrm{2} \\ $$$${s}_{{n}} \leqslant\mathrm{2}\sqrt{{n}}−\mathrm{1},\mathrm{2}\sqrt{{n}+\mathrm{1}}−\mathrm{1}\leqslant{s}_{{n}} \\ $$$$\frac{\sqrt{{n}+\mathrm{1}}}{\:\sqrt{{n}}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{{n}}}\leqslant\frac{{s}_{{n}} }{\mathrm{2}\sqrt{{n}}}\leqslant\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{{n}}} \\ $$$${n}\rightarrow\infty \\ $$$$\Rightarrow{S}_{{n}} \sim\mathrm{2}\sqrt{{n}} \\ $$
Commented by mathmax by abdo last updated on 19/Feb/21

$$\mathrm{thanks}\:\mathrm{sir}\:\mathrm{mind} \\ $$
