Question Number 75220 by ~blr237~ last updated on 08/Dec/19
$$\mathrm{Let}\:\mathrm{us}\:\mathrm{consider}\:\mathrm{the}\:\mathrm{function}\: \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{lnt}\right)\mathrm{dt}\: \\ $$$$\left.\mathrm{1}\right)\mathrm{Prove}\:\mathrm{that}\:\mathrm{for}\:\mathrm{all}\:\mathrm{x}\geqslant\mathrm{1}\:,\:\:\mathrm{F}\left(\mathrm{x}\right)\:\mathrm{exist} \\ $$$$\left.\mathrm{2}\right)\mathrm{Prove}\:\mathrm{that}\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{tln}\left(\mathrm{x}−\mathrm{lnt}\right)=\mathrm{0} \\ $$$$\left.\mathrm{3}\right)\mathrm{Prove}\:\mathrm{that}\:\mathrm{F}\:\in\:\mathrm{C}^{\mathrm{1}} \left(\left[\mathrm{1}:\infty\left[,\left[\mathrm{1}:\infty\left[\right)\:\mathrm{and}\:\mathrm{for}\:\right.\right.\right.\right. \\ $$$$\mathrm{all}\:\mathrm{x}\geqslant\mathrm{1}\:\:\mathrm{F}\left(\mathrm{x}\right)=\mathrm{F}'\left(\mathrm{x}\right)+\mathrm{lnx} \\ $$$$\left.\mathrm{4}\right)\:\mathrm{Find}\:\mathrm{out}\:\mathrm{the}\:\mathrm{value}\: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{F}\left(\mathrm{x}\right)\:\:\:\:\:\:\mathrm{and}\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}F}\left(\mathrm{x}\right) \\ $$$$\left.\mathrm{5}\right)\mathrm{Can}\:\mathrm{you}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{at}\:\mathrm{least}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{both}\:\mathrm{result}\:\mathrm{is}\:\mathrm{irrational}??? \\ $$
Answered by mind is power last updated on 08/Dec/19
![mistak at 3) F(x)=∫_0 ^1 e^(−x) ln(x−ln(t))dt F′(x)=∫_0 ^1 {−e^(−x) ln(x−ln(t))+(e^(−x) /(x−ln(t)))}dt by part F(x)=e^(−x) ∫_0 ^1 1.ln(x−ln(t))dt F(x)=e^(−x) {[tln(x−ln(t))]_0 ^1 −∫_0 ^1 t.((−1)/t).(dt/(x−ln(t)))} =e^(−x) ln(x)+e^(−x) ∫_0 ^1 (dt/(x−ln(t))) ⇒F(x)−F′(x)=∫_0 ^1 e^(−x) ln(x−ln(t))dt+e^(−x) ln(x) ⇔−F′(x)=e^(−x) ln(x) ⇒F′(x)=−e^(−x) ln(x)](https://www.tinkutara.com/question/Q75234.png)
$$\left.\mathrm{mistak}\:\mathrm{at}\:\mathrm{3}\right) \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\mathrm{dt} \\ $$$$\mathrm{F}'\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \left\{−\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)+\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)}\right\}\mathrm{dt} \\ $$$$\mathrm{by}\:\mathrm{part}\:\mathrm{F}\left(\mathrm{x}\right)=\mathrm{e}^{−\mathrm{x}} \int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{1}.\mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\mathrm{dt} \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\mathrm{e}^{−\mathrm{x}} \left\{\left[\mathrm{tln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{t}.\frac{−\mathrm{1}}{\mathrm{t}}.\frac{\mathrm{dt}}{\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)}\right\} \\ $$$$=\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right)+\mathrm{e}^{−\mathrm{x}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dt}}{\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)} \\ $$$$\Rightarrow\mathrm{F}\left(\mathrm{x}\right)−\mathrm{F}'\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\mathrm{dt}+\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right) \\ $$$$\Leftrightarrow−\mathrm{F}'\left(\mathrm{x}\right)=\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\mathrm{F}'\left(\mathrm{x}\right)=−\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right) \\ $$
Commented by ~blr237~ last updated on 08/Dec/19
$$\mathrm{Sorry}\:\:\mathrm{it}'\mathrm{s}\:\mathrm{because}\:,\:\mathrm{i}\:\mathrm{started}\:\mathrm{my}\:\mathrm{work}\:\:\mathrm{with}\:\:\mathrm{G}\left(\mathrm{x}\right)=\mathrm{e}^{\mathrm{x}} \mathrm{F}\left(\mathrm{x}\right)\: \\ $$$$\mathrm{and}\:\mathrm{it}\:\mathrm{was}\:\:\mathrm{G}\left(\mathrm{x}\right)=\mathrm{G}'\left(\mathrm{x}\right)+\mathrm{lnx}\:.\: \\ $$
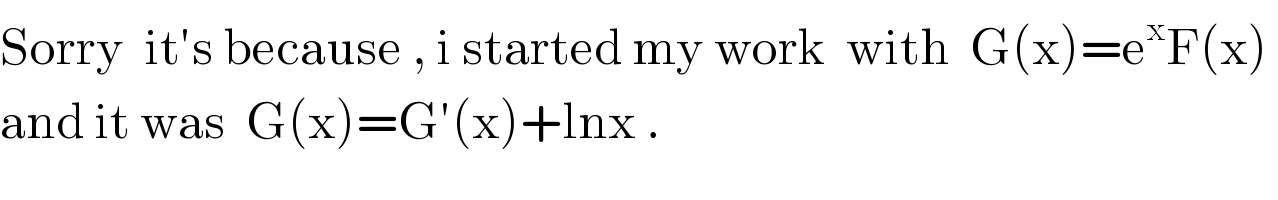
Commented by mind is power last updated on 08/Dec/19
$$\mathrm{F}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\mathrm{dt}? \\ $$
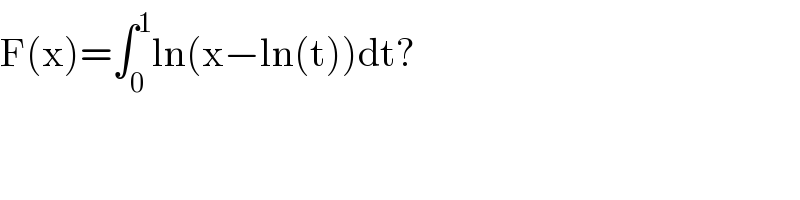
Commented by ~blr237~ last updated on 09/Dec/19
$$\mathrm{yes} \\ $$
Answered by mind is power last updated on 09/Dec/19
![F(x )=∫_0 ^1 e^(−x) ln(x−ln(t))dt uf x≥1⇒x−ln(t)≥1 ,∀t∈[0,1] 1≤ln(x−ln(t))=ln(x)+ln(1−((ln(t))/x))≤ln(x)−((ln(t))/x)≤ln(x) 0≤∫_0 ^1 e^(−x) ln(x−ln(t))dt≤e^(−x) ∫_0 ^1 (ln(x)−((ln(t))/x))dt=(ln(x)+(1/x))e^(−x) ⇒F(x) exist 2) ∀(x,t)∈[1,+∞[×[0,1] 0≤tln(x−ln(t))≤t ln(x)−((tln(t))/x) lim tln(x)−((tln(t))/x)→0 ⇒t ln(x−ln(t))→0 3) F is C_1 F is continous (x,t)→e^(−x) ln(x−ln(t)) is continous in each variable e^(−x) ln(x−ln(t))≤e^(−x) {ln(x)+ln(1−((ln(t))/x))}≤e^(−x) {ln(x)−((ln(t))/x)} ≤e^(−x) ln(x)+(e^(−x) /x){−ln(t)} e^(−x) ln(x)≤1,∀x≥1 (e^(−x) /x)≤1 ,∀x≥1⇒e^(−x) ln(x−ln(t))≤1−ln(t)=g(t) ⇒e^(−x) ln(x−ln(t))≤(1−ln(t))=g(t) witch is integrBl in ]0,1[ (t,x)→(∂/∂x)(e^(−x) ln(x−ln(t))) continus (t,x)→(∂/∂t)(e^(−x) ln(x−ln(t)))continus over [0,1[ (∂/∂x)(e^(−x) ln(x−ln(t)))=−e^(−x) ln(x−ln(t))+(e^(−x) /(x−ln(t))) x−ln(t)≥1⇒(e^(−x) /(x−ln(t)))≤e^(−x) ≤1 ln(x−ln(t))=ln(x)+ln(1−((ln(t))/x))≤ln(x)−((ln(t))/x) ⇒∣(∂/∂x)(e^(−x) ln(x−ln(t)))∣≤e^(−x) ln(x−ln(t))+1≤e^(−x) ln(x)+e^(−x) .((−ln(t))/x)+1 ≤3−ln(t) =g(t) ⇒∀x∈[1,+∞[ ∫∣(∂/∂x)(e^(−x) ln(x−ln(t))∣dt≤∫_0 ^1 g(t)dt=4 ⇒F(x) is C_1 g(x)=e^x F(x) g(x) is C_1 since F(x) and e^x are g(x)=∫_0 ^1 ln(x−ln(t))dt g(x)=∫_0 ^1 1.ln(x−ln(t))dt by part ⇒g(x)=[tln(x−ln(t))]_0 ^1 +∫(1/t).(t/(x−ln(t)))dt g(x)=ln(x)+∫(dt/(x−ln(t))) g′(x)=∫_0 ^1 (∂/∂x)(ln(x−ln(t))dt g′(x)=∫_0 ^1 (dt/(x−ln(t))) g(x)=ln(x)+g′(x)⇔g(x)=g′(x)+ln(x) g is continous lim_(x→∞) F(x)=lim_(x→∞) ∫_0 ^1 ln(x−ln(t))dt=lim_(x→∞) ∫_0 ^1 (dt/(x−ln(t))) x−ln(t)≥x⇒ ≤lim_(x→∞) ∫_0 ^1 (dt/x)=lim_(x→∞) (1/x)=0 since G(x) is C_1 ⇒lim_(x→1) G(x)=G(1)⇒ lim_(x→1) ∫_0 ^1 (dt/(x−ln(t)))=∫_0 ^1 (dt/(1−ln(t))) u=−ln(t)⇒G(1)=∫_0 ^(+∞) (e^(−u) /(1+u))](https://www.tinkutara.com/question/Q75282.png)
$$\mathrm{F}\left(\mathrm{x}\:\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\mathrm{dt} \\ $$$$\mathrm{uf}\:\mathrm{x}\geqslant\mathrm{1}\Rightarrow\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\geqslant\mathrm{1}\:,\forall\mathrm{t}\in\left[\mathrm{0},\mathrm{1}\right] \\ $$$$\mathrm{1}\leqslant\mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)=\mathrm{ln}\left(\mathrm{x}\right)+\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{x}}\right)\leqslant\mathrm{ln}\left(\mathrm{x}\right)−\frac{\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{x}}\leqslant\mathrm{ln}\left(\mathrm{x}\right) \\ $$$$\mathrm{0}\leqslant\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\mathrm{dt}\leqslant\mathrm{e}^{−\mathrm{x}} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{ln}\left(\mathrm{x}\right)−\frac{\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{x}}\right)\mathrm{dt}=\left(\mathrm{ln}\left(\mathrm{x}\right)+\frac{\mathrm{1}}{\mathrm{x}}\right)\mathrm{e}^{−\mathrm{x}} \\ $$$$\Rightarrow\mathrm{F}\left(\mathrm{x}\right)\:\mathrm{exist} \\ $$$$\left.\mathrm{2}\right)\:\forall\left(\mathrm{x},\mathrm{t}\right)\in\left[\mathrm{1},+\infty\left[×\left[\mathrm{0},\mathrm{1}\right]\right.\right. \\ $$$$\mathrm{0}\leqslant\mathrm{tln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\leqslant\mathrm{t}\:\mathrm{ln}\left(\mathrm{x}\right)−\frac{\mathrm{tln}\left(\mathrm{t}\right)}{\mathrm{x}} \\ $$$$\mathrm{lim}\:\:\mathrm{tln}\left(\mathrm{x}\right)−\frac{\mathrm{tln}\left(\mathrm{t}\right)}{\mathrm{x}}\rightarrow\mathrm{0} \\ $$$$\Rightarrow\mathrm{t}\:\mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\rightarrow\mathrm{0} \\ $$$$\left.\mathrm{3}\right)\:\mathrm{F}\:\mathrm{is}\:\mathrm{C}_{\mathrm{1}} \\ $$$$\mathrm{F}\:\mathrm{is}\:\mathrm{continous}\: \\ $$$$\left(\mathrm{x},\mathrm{t}\right)\rightarrow\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\:\mathrm{is}\:\mathrm{continous}\:\mathrm{in}\:\mathrm{each}\:\mathrm{variable} \\ $$$$\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\leqslant\mathrm{e}^{−\mathrm{x}} \left\{\mathrm{ln}\left(\mathrm{x}\right)+\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{x}}\right)\right\}\leqslant\mathrm{e}^{−\mathrm{x}} \left\{\mathrm{ln}\left(\mathrm{x}\right)−\frac{\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{x}}\right\} \\ $$$$\leqslant\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right)+\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{x}}\left\{−\mathrm{ln}\left(\mathrm{t}\right)\right\} \\ $$$$\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right)\leqslant\mathrm{1},\forall\mathrm{x}\geqslant\mathrm{1}\: \\ $$$$\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{x}}\leqslant\mathrm{1}\:,\forall\mathrm{x}\geqslant\mathrm{1}\Rightarrow\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\leqslant\mathrm{1}−\mathrm{ln}\left(\mathrm{t}\right)=\mathrm{g}\left(\mathrm{t}\right) \\ $$$$\left.\Rightarrow\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\leqslant\left(\mathrm{1}−\mathrm{ln}\left(\mathrm{t}\right)\right)=\mathrm{g}\left(\mathrm{t}\right)\:\mathrm{witch}\:\mathrm{is}\:\mathrm{integrBl}\:\mathrm{in}\:\right]\mathrm{0},\mathrm{1}\left[\right. \\ $$$$\left(\mathrm{t},\mathrm{x}\right)\rightarrow\frac{\partial}{\partial\mathrm{x}}\left(\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\right)\:\mathrm{continus} \\ $$$$\left(\mathrm{t},\mathrm{x}\right)\rightarrow\frac{\partial}{\partial\mathrm{t}}\left(\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\right)\mathrm{continus}\:\:\mathrm{over}\:\left[\mathrm{0},\mathrm{1}\left[\right.\right. \\ $$$$\frac{\partial}{\partial\mathrm{x}}\left(\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\right)=−\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)+\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)} \\ $$$$\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\geqslant\mathrm{1}\Rightarrow\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)}\leqslant\mathrm{e}^{−\mathrm{x}} \leqslant\mathrm{1} \\ $$$$\mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)=\mathrm{ln}\left(\mathrm{x}\right)+\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{x}}\right)\leqslant\mathrm{ln}\left(\mathrm{x}\right)−\frac{\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{x}} \\ $$$$\Rightarrow\mid\frac{\partial}{\partial\mathrm{x}}\left(\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\right)\mid\leqslant\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)+\mathrm{1}\leqslant\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right)+\mathrm{e}^{−\mathrm{x}} .\frac{−\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{x}}+\mathrm{1} \\ $$$$\leqslant\mathrm{3}−\mathrm{ln}\left(\mathrm{t}\right)\:=\mathrm{g}\left(\mathrm{t}\right) \\ $$$$\Rightarrow\forall\mathrm{x}\in\left[\mathrm{1},+\infty\left[\:\:\:\int\mid\frac{\partial}{\partial\mathrm{x}}\left(\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\mid\mathrm{dt}\leqslant\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{g}\left(\mathrm{t}\right)\mathrm{dt}=\mathrm{4}\right.\right.\right. \\ $$$$\Rightarrow\mathrm{F}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{C}_{\mathrm{1}} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\mathrm{e}^{\mathrm{x}} \mathrm{F}\left(\mathrm{x}\right) \\ $$$$\mathrm{g}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{C}_{\mathrm{1}} \:\mathrm{since}\:\mathrm{F}\left(\mathrm{x}\right)\:\mathrm{and}\:\mathrm{e}^{\mathrm{x}} \:\mathrm{are} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\mathrm{dt} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{1}.\mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\mathrm{dt}\:\mathrm{by}\:\mathrm{part} \\ $$$$\Rightarrow\mathrm{g}\left(\mathrm{x}\right)=\left[\mathrm{tln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\int\frac{\mathrm{1}}{\mathrm{t}}.\frac{\mathrm{t}}{\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)}\mathrm{dt} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\mathrm{ln}\left(\mathrm{x}\right)+\int\frac{\mathrm{dt}}{\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)} \\ $$$$\mathrm{g}'\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\partial}{\partial\mathrm{x}}\left(\mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\mathrm{dt}\right. \\ $$$$\mathrm{g}'\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dt}}{\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)}\: \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\mathrm{ln}\left(\mathrm{x}\right)+\mathrm{g}'\left(\mathrm{x}\right)\Leftrightarrow\mathrm{g}\left(\mathrm{x}\right)=\mathrm{g}'\left(\mathrm{x}\right)+\mathrm{ln}\left(\mathrm{x}\right) \\ $$$$\mathrm{g}\:\mathrm{is}\:\mathrm{continous} \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}F}\left(\mathrm{x}\right)=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\right)\mathrm{dt}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dt}}{\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)} \\ $$$$\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)\geqslant\mathrm{x}\Rightarrow \\ $$$$\leqslant\underset{{x}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dt}}{\mathrm{x}}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{0} \\ $$$$\mathrm{since}\:\mathrm{G}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{C}_{\mathrm{1}} \Rightarrow\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}G}\left(\mathrm{x}\right)=\mathrm{G}\left(\mathrm{1}\right)\Rightarrow \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dt}}{\mathrm{x}−\mathrm{ln}\left(\mathrm{t}\right)}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dt}}{\mathrm{1}−\mathrm{ln}\left(\mathrm{t}\right)} \\ $$$$\mathrm{u}=−\mathrm{ln}\left(\mathrm{t}\right)\Rightarrow\mathrm{G}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{e}^{−\mathrm{u}} }{\mathrm{1}+\mathrm{u}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$