Question Number 73473 by mathmax by abdo last updated on 13/Nov/19
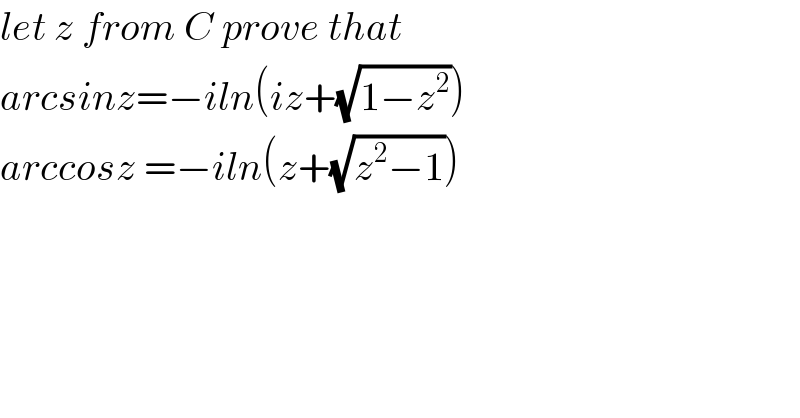
$${let}\:{z}\:{from}\:{C}\:{prove}\:{that}\: \\ $$$${arcsinz}=−{iln}\left({iz}+\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }\right) \\ $$$${arccosz}\:=−{iln}\left({z}+\sqrt{{z}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$
Commented by mathmax by abdo last updated on 15/Nov/19
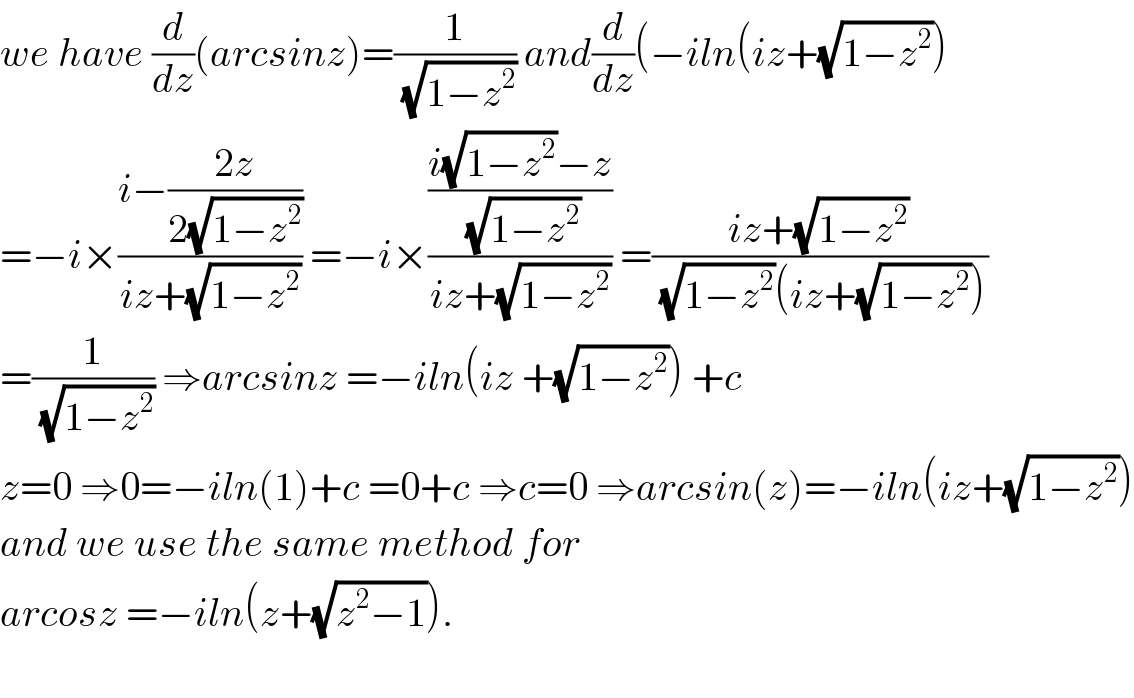
$${we}\:{have}\:\frac{{d}}{{dz}}\left({arcsinz}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }}\:{and}\frac{{d}}{{dz}}\left(−{iln}\left({iz}+\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }\right)\right. \\ $$$$=−{i}×\frac{{i}−\frac{\mathrm{2}{z}}{\mathrm{2}\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }}}{{iz}+\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }}\:=−{i}×\frac{\frac{{i}\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }−{z}}{\:\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }}}{{iz}+\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }}\:=\frac{{iz}+\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }\left({iz}+\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }\right)} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }}\:\Rightarrow{arcsinz}\:=−{iln}\left({iz}\:+\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }\right)\:+{c} \\ $$$${z}=\mathrm{0}\:\Rightarrow\mathrm{0}=−{iln}\left(\mathrm{1}\right)+{c}\:=\mathrm{0}+{c}\:\Rightarrow{c}=\mathrm{0}\:\Rightarrow{arcsin}\left({z}\right)=−{iln}\left({iz}+\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }\right) \\ $$$${and}\:{we}\:{use}\:{the}\:{same}\:{method}\:{for} \\ $$$${arcosz}\:=−{iln}\left({z}+\sqrt{{z}^{\mathrm{2}} −\mathrm{1}}\right). \\ $$$$ \\ $$
