lets-A-and-B-be-two-finite-sets-proof-or-give-a-counter-example-that-A-B-A-B-A-B-

Question Number 1672 by 123456 last updated on 30/Aug/15

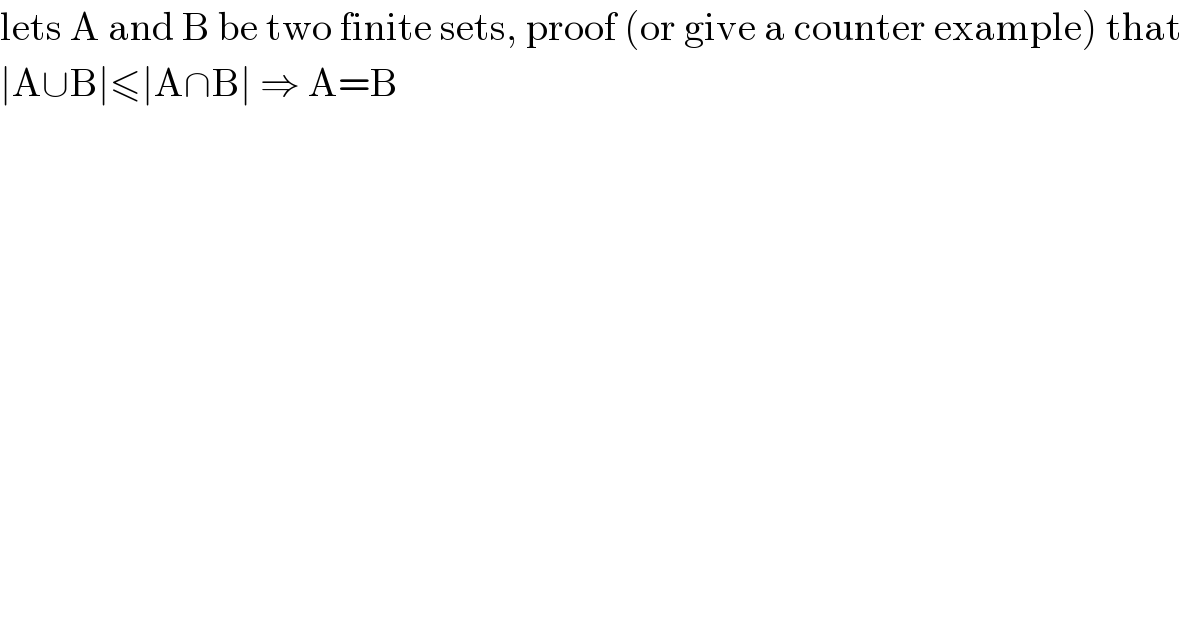
$$\mathrm{lets}\:\mathrm{A}\:\mathrm{and}\:\mathrm{B}\:\mathrm{be}\:\mathrm{two}\:\mathrm{finite}\:\mathrm{sets},\:\mathrm{proof}\:\left(\mathrm{or}\:\mathrm{give}\:\mathrm{a}\:\mathrm{counter}\:\mathrm{example}\right)\:\mathrm{that} \\ $$$$\mid\mathrm{A}\cup\mathrm{B}\mid\leqslant\mid\mathrm{A}\cap\mathrm{B}\mid\:\Rightarrow\:\mathrm{A}=\mathrm{B} \\ $$

Answered by Rasheed Soomro last updated on 01/Sep/15

$$\boldsymbol{\mathrm{Case}}−\mathrm{1}\:\boldsymbol{\mathrm{W}}\mathrm{hen}\:\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}=\varnothing\:,\:\mid\:\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\mid=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{SubCase}}\:\:\left(\boldsymbol{\mathrm{a}}\right)\:\boldsymbol{\mathrm{At}}\:\boldsymbol{\mathrm{least}}\:\boldsymbol{\mathrm{one}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{A}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{B}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{nonempty}}. \\ $$$$\:\:\:\:\:\:\:\mathrm{Say}\:\boldsymbol{\mathrm{A}}\:\mathrm{is}\:\mathrm{nonempty} \\ $$$$\:\:\:\:\:\:\:\mid\:\boldsymbol{\mathrm{A}}\:\mid>\mathrm{0}\:\wedge\:\mid\:\boldsymbol{\mathrm{B}}\:\mid\geqslant\mathrm{0}\:\Rightarrow\mid\:\boldsymbol{\mathrm{A}}\:\mid+\mid\:\boldsymbol{\mathrm{B}}\:\mid>\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\mid\:\boldsymbol{\mathrm{A}}\:\cup\boldsymbol{\mathrm{B}}\:\mid=\mid\:\boldsymbol{\mathrm{A}}\:\mid+\mid\:\boldsymbol{\mathrm{B}}\:\mid>\mathrm{0}\:\:\:\:\left[\boldsymbol{\mathrm{A}}\:\mathrm{and}\:\boldsymbol{\mathrm{B}}\:\mathrm{are}\:\mathrm{disjoint}\:\mathrm{sets}.\right]….\boldsymbol{\mathrm{I}} \\ $$$$\:\:\:\:\:\:\:\mid\:\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\mid=\mathrm{0}…………………………………………………….\boldsymbol{\mathrm{II}} \\ $$$$\mid\:\mathrm{A}\cup\boldsymbol{\mathrm{B}}\:\mid>\mid\:\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\mid\:\:\:\:\:\:\:\:\:\:\left[\mathrm{From}\:\:\boldsymbol{\mathrm{I}}\:\:\mathrm{and}\:\:\boldsymbol{\mathrm{II}}\right]\mid \\ $$$$\:\:\:\:\:\:\:\mathrm{In}\:\mathrm{this}\:\mathrm{subcase}\:\:\mid\:\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid\:\nleq\:\mid\:\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\mid \\ $$$$\:\:\:\:\:\:\boldsymbol{\mathrm{Not}}\:\boldsymbol{\mathrm{concerned}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{result}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{prove}}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{SubCase}}\:\:\left(\boldsymbol{\mathrm{b}}\right)\boldsymbol{\mathrm{When}}\:\boldsymbol{\mathrm{A}}=\varnothing\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{B}}=\boldsymbol{\varnothing}\:,\:\mid\:\boldsymbol{\mathrm{A}}\:\mid=\mathrm{0}\:\mathrm{and}\:\mid\boldsymbol{\mathrm{B}}\:\mid=\mathrm{0}. \\ $$$$\:\:\:\:\:\:\:\mid\:\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\:\mid=\mid\:\boldsymbol{\mathrm{A}}\:\mid+\mid\:\boldsymbol{\mathrm{B}}\:\mid=\mathrm{0}+\mathrm{0}=\mathrm{0}\:\:\:………………………..\boldsymbol{\mathrm{I}} \\ $$$$\:\:\:\:\:\:\:\mid\:\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\mid=\mathrm{0}………………………………………………..\boldsymbol{\mathrm{II}} \\ $$$$\:\:\:\:\:\:\:\mid\:\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\:\mid=\:\mid\:\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\mid\Rightarrow\boldsymbol{\mathrm{A}}=\boldsymbol{\mathrm{B}}=\boldsymbol{\varnothing}\:\:\:\:\:\:\:\:\:\:\left[\mathrm{From}\:\:\boldsymbol{\mathrm{I}}\:\:\mathrm{and}\:\:\boldsymbol{\mathrm{II}}\right] \\ $$$$\:\:\:\:\:\:\:\:\mid\:\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\:\mid=\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\:\mid\Rightarrow\:\boldsymbol{\mathrm{A}}=\boldsymbol{\mathrm{B}} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{Proved}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{result}}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{this}}\:\boldsymbol{\mathrm{subcase}}. \\ $$$$\boldsymbol{\mathrm{Case}}−\mathrm{2}\:\boldsymbol{\mathrm{When}}\:\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\neq\boldsymbol{\varnothing}\:\:\boldsymbol{\mathrm{i}}−\boldsymbol{\mathrm{e}}\:\boldsymbol{\mathrm{A}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{B}}\:\boldsymbol{\mathrm{are}}\:\boldsymbol{\mathrm{overlapping}}\:\boldsymbol{\mathrm{sets}}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{SubCase}}\:\left(\boldsymbol{\mathrm{a}}\right)\:\boldsymbol{\mathrm{A}}\:\varsubsetneq\:\boldsymbol{\mathrm{B}}\:\:\wedge\:\boldsymbol{\mathrm{B}}\:\varsubsetneq\:\boldsymbol{\mathrm{A}}\:{means}\:\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\subseteq\:\boldsymbol{\mathrm{A}}\:\wedge\:\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\subseteq\boldsymbol{\mathrm{B}} \\ $$$$\:\:\:\:\:\:\:\mid\:\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\:\mid=\mid\boldsymbol{\mathrm{A}}\mid+\mid\boldsymbol{\mathrm{B}}\mid−\mid\:\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\mid\: \\ $$$$\:\:\:\: \\ $$$$\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\subset\:\boldsymbol{\mathrm{A}}\Rightarrow\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\mid<\:\mid\boldsymbol{\mathrm{A}}\mid\:\:\:,\:\:\:\:\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\subset\:\boldsymbol{\mathrm{B}}\Rightarrow\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\:<\:\mid\boldsymbol{\mathrm{B}}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\mathrm{2}\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid<\mid\boldsymbol{\mathrm{A}}\mid+\mid\boldsymbol{\mathrm{B}}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\:<\mid\boldsymbol{\mathrm{A}}\mid+\mid\boldsymbol{\mathrm{B}}\mid−\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid<\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\Rightarrow\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid>\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid \\ $$$$\:\:\boldsymbol{\mathrm{Not}}\:\boldsymbol{\mathrm{concerned}}\:\boldsymbol{\mathrm{with}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{result}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{prove}}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{SubCase}}\:\:\left(\boldsymbol{\mathrm{b}}\right)\:\boldsymbol{\mathrm{One}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{A}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{B}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{subset}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{other}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{Say}}\:\boldsymbol{\mathrm{A}}\subseteq\boldsymbol{\mathrm{B}}\:\Rightarrow\:\mid\boldsymbol{\mathrm{A}}\mid\leqslant\mid\boldsymbol{\mathrm{B}}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\:=\boldsymbol{\mathrm{B}}\Rightarrow\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid=\mid\boldsymbol{\mathrm{B}}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:=\boldsymbol{\mathrm{A}}\Rightarrow\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid=\mid\boldsymbol{\mathrm{A}}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\boldsymbol{\mathrm{A}}\mid\leqslant\mid\boldsymbol{\mathrm{B}}\mid\Rightarrow\:\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\leqslant\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid\Rightarrow\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid\geqslant\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\underset{{Not}\:{concerned}} {\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid>\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid}\:\:\:\:\vee\:\:\:\:\:\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid=\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{SubCase}}\:\:\:\left(\boldsymbol{\mathrm{c}}\right)\:\:\boldsymbol{\mathrm{A}}\subseteq\boldsymbol{\mathrm{B}}\:\wedge\:\boldsymbol{\mathrm{B}}\subseteq\boldsymbol{\mathrm{A}}\:\:\:\:\boldsymbol{\mathrm{i}}−\boldsymbol{\mathrm{e}}\:\:\:\:\boldsymbol{\mathrm{A}}=\boldsymbol{\mathrm{B}} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\boldsymbol{\mathrm{Continue}} \\ $$

Answered by Rasheed Soomro last updated on 01/Sep/15

$$\mid\mathrm{A}\cup\mathrm{B}\mid\leqslant\mid\mathrm{A}\cap\mathrm{B}\mid\:\Rightarrow\:\mathrm{A}=\mathrm{B} \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow\:\underset{−} {\mid\mathrm{A}\cup\mathrm{B}\mid<\mid\mathrm{A}\cap\mathrm{B}\mid\:\Rightarrow\:\mathrm{A}=\mathrm{B}}\:\vee\:\underset{−} {\mid\mathrm{A}\cup\mathrm{B}\mid=\mid\mathrm{A}\cap\mathrm{B}\mid\:\Rightarrow\:\mathrm{A}=\mathrm{B}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\mathrm{First}\:\mathrm{we}\:\mathrm{will}\:\mathrm{prove}\:\mathrm{that}\left[\:\underset{−} {\mid\mathrm{A}\cup\mathrm{B}\mid<\mid\mathrm{A}\cap\mathrm{B}\mid\:\Rightarrow\:\mathrm{A}=\mathrm{B}}\:\right]\:\mathrm{is}\:\mathrm{false} \\ $$$$\mathrm{for}\:\mathrm{any}\:\boldsymbol{\mathrm{A}}\:\mathrm{and}\:\boldsymbol{\mathrm{B}}.\:\mathrm{Then}\:\mathrm{we}\:\mathrm{will}\:\mathrm{prove}\:\:: \\ $$$$\underset{−} {\mid\mathrm{A}\cup\mathrm{B}\mid=\mid\mathrm{A}\cap\mathrm{B}\mid\:\Rightarrow\:\mathrm{A}=\mathrm{B}} \\ $$$$ \\ $$$$\begin{cases}{\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\subseteq\:\boldsymbol{\mathrm{A}}}\\{\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\subseteq\:\boldsymbol{\mathrm{B}}}\end{cases}\Rightarrow\begin{cases}{\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\mid\leqslant\:\mid\boldsymbol{\mathrm{A}}\mid}\\{\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\mid\leqslant\:\mid\boldsymbol{\mathrm{B}}\mid}\end{cases}\Rightarrow\mathrm{2}\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\leqslant\mid\boldsymbol{\mathrm{A}}\mid+\mid\boldsymbol{\mathrm{B}}\mid \\ $$$$\Rightarrow\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\:\leqslant\:\mid\boldsymbol{\mathrm{A}}\mid+\mid\boldsymbol{\mathrm{B}}\mid−\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid \\ $$$$\Rightarrow\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\leqslant\:\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid\:\:\:\:\:\:\:\:\:\:\left[\:\because\:\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid=\mid\boldsymbol{\mathrm{A}}\mid+\mid\boldsymbol{\mathrm{B}}\mid−\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\:\right] \\ $$$$\Rightarrow\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid\:\geqslant\:\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid \\ $$$$\Rightarrow\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid\nless\:\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid \\ $$$$ \\ $$$$\boldsymbol{\mathrm{Proof}}\:\boldsymbol{\mathrm{for}}\:\:\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid=\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\:\:\Rightarrow\:\:\boldsymbol{\mathrm{A}}=\boldsymbol{\mathrm{B}}\:\: \\ $$$$\:\:\:\:\:\mathrm{On}\:\mathrm{the}\:\mathrm{contrary}\:\mathrm{suppose}\:\boldsymbol{\mathrm{A}}\neq\boldsymbol{\mathrm{B}} \\ $$$$\mathrm{Then}\:\mathrm{there}\:\mathrm{must}\:\mathrm{be}\:\mathrm{a}\:\mathrm{member}\:\mathrm{x}\:\mathrm{which}\:\mathrm{belongs}\:\mathrm{to} \\ $$$$\mathrm{one}\:\mathrm{of}\:\boldsymbol{\mathrm{A}}\:\mathrm{and}\:\boldsymbol{\mathrm{B}}\:\mathrm{and}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{belong}\:\mathrm{to}\:\mathrm{other}. \\ $$$$\mathrm{Say}\:\mathrm{x}\:\in\:\boldsymbol{\mathrm{A}}\:\wedge\:\mathrm{x}\:\notin\:\boldsymbol{\mathrm{B}} \\ $$$$\Rightarrow\:\mathrm{x}\:\in\:\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\:\mathrm{but}\:\mathrm{x}\:\notin\:\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}} \\ $$$$\Rightarrow\:\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid\neq\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid \\ $$$$\mathrm{Which}\:\mathrm{contradicts}\:\mathrm{the}\:\mathrm{given}\:\left[\:\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid=\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\:\right] \\ $$$$\mathrm{Hence}\:\:\:\boldsymbol{\mathrm{A}}=\boldsymbol{\mathrm{B}}\:\:\:\:\:\left({proved}\right) \\ $$$$\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid=\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\:\:\Rightarrow\:\:\boldsymbol{\mathrm{A}}=\boldsymbol{\mathrm{B}}\:\:\:\:\left(\boldsymbol{\mathrm{More}}\:\boldsymbol{\mathrm{specific}}\right) \\ $$$$\boldsymbol{\mathrm{Or}}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{say}}\:\boldsymbol{\mathrm{also}}, \\ $$$$\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid\leqslant\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\:\:\Rightarrow\:\:\boldsymbol{\mathrm{A}}=\boldsymbol{\mathrm{B}}\:\:\:\:\left(\boldsymbol{\mathrm{Not}}\:\boldsymbol{\mathrm{specific}}\right) \\ $$

Commented by 112358 last updated on 01/Sep/15

$${In}\:{your}\:{proof}\:{of}\:\mid{A}\cup{B}\mid=\mid{A}\cap{B}\mid\Rightarrow{A}={B} \\ $$$${you}\:{correctly}\:{proved}\:{the}\:{implication} \\ $$$${by}\:{proving}\:{the}\:{contrapositive}\:{of} \\ $$$${the}\:{statement}\:\left({A}\neq{B}\Rightarrow\mid{A}\cup{B}\mid\neq\mid{A}\cap{B}\mid\right). \\ $$$${But},\:{I}\:{was}\:{confused}\:{a}\:{bit}\:{when}\: \\ $$$${reading}\:{it}\:{where}\:{you}\:{said}\:'{Which} \\ $$$${contradicts}!'\:{because}\:{then}\:{it}\:{sounds} \\ $$$${as}\:{if}\:{the}\:{result}\:{is}\:{never}\:{true}\:{given}\:{A}\neq{B},{which} \\ $$$${is}\:{employed}\:{in}\:{the}\:{method}\:{of}\: \\ $$$${proof}\:{by}\:{contradiction}.\:{It}\:{doesn}'{t} \\ $$$${seem}\:{necessary}\:{to}\:{put}\:{in}\:{that}\:{line} \\ $$$${of}\:{text}.\:{You}\:{finished}\:{the}\:{essence} \\ $$$${of}\:{the}\:{proof}\:{when}\:{you}\:{showed} \\ $$$${that}\:\mid{A}\cup{B}\mid\neq\mid{A}\cap{B}\mid. \\ $$$${p}\Rightarrow{q}\:{is}\:{logically}\:{equivalent}\:{to} \\ $$$$\backsim{q}\Rightarrow\backsim{p}.\: \\ $$

Commented by 112358 last updated on 01/Sep/15

$${Very}\:{good}\:{analysis}\:{overall}! \\ $$

Commented by Rasheed Soomro last updated on 01/Sep/15

$$\mathrm{Thank}\mathbb{S}\boldsymbol{\mathrm{Sss}}{ssss}\:\mathrm{for}\:\mathrm{guidance}! \\ $$$$\mathrm{Use}\:\mathrm{of}\:\mathrm{proper}\:\mathrm{language}\:\mathrm{in}\:\mathbb{M}\mathrm{athematics},\:\mathrm{specially}\:\mathrm{in}\:\mathrm{logic} \\ $$$$\mathrm{is}\:\mathrm{basic}\:\mathrm{need}.\:\mathrm{I}\:\mathrm{am}\:\mathrm{not}\:\mathrm{much}\:\mathrm{confident}\:\mathrm{regarding}\:\mathrm{language}. \\ $$$$\mathrm{However}\:\:\mathrm{in}\:\mathrm{above}\:\mathrm{answer}\:\mathrm{by}\:'\:\mathrm{Which}\:\mathrm{contradicts}\:'\:\mathrm{I}\:\mathrm{mean}\: \\ $$$$\mathrm{contradicts}\:\mathrm{the}\:\mathrm{given}.\:\mathrm{If}\:\mathrm{P}\:\mathrm{is}\:\mathrm{given}\:\mathrm{and}\:\mathrm{you}\:\mathrm{reached}\:\mathrm{at}\:\sim\mathrm{P} \\ $$$$\mathrm{what}\:\mathrm{should}\:\mathrm{you}\:\mathrm{say}!\:\mathrm{Given}\:\mathrm{is}\:\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid=\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\:\mathrm{but}\:\mathrm{you}\:\mathrm{reached} \\ $$$$\mathrm{at}\:\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid\neq\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid.\:\mathrm{Is}\:\mathrm{this}\:\mathrm{not}\:\mathrm{contradiction}? \\ $$$$\:\mathrm{Anyway}\:\mathrm{you}\:\mathrm{have}\:\mathrm{provided}\:\mathrm{a}\:\mathrm{good}\:\:\mathrm{alternate}\:\mathrm{way}\:\mathrm{of}\:\mathrm{saying}\: \\ $$$$\mathrm{same}\:\mathrm{thing}! \\ $$

Commented by 123456 last updated on 01/Sep/15

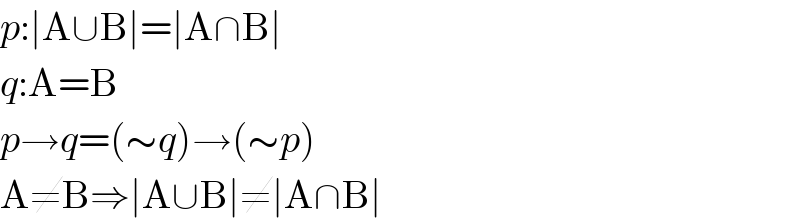
$${p}:\mid\mathrm{A}\cup\mathrm{B}\mid=\mid\mathrm{A}\cap\mathrm{B}\mid \\ $$$${q}:\mathrm{A}=\mathrm{B} \\ $$$${p}\rightarrow{q}=\left(\sim{q}\right)\rightarrow\left(\sim{p}\right) \\ $$$$\mathrm{A}\neq\mathrm{B}\Rightarrow\mid\mathrm{A}\cup\mathrm{B}\mid\neq\mid\mathrm{A}\cap\mathrm{B}\mid \\ $$

Commented by 112358 last updated on 01/Sep/15

$${Yes}.\:{I}\:{understand}\:{what}\:{you}\:{mean}. \\ $$$${Ijust}\:{saw}\:{the}\:{correction}\:{you}\:{made}. \\ $$$${I}\:{now}\:{see}\:{how}\:{you}\:{decided}\:{to} \\ $$$${argue}\:{the}\:{proof}\:{in}\:{such}\:{a}\:{way} \\ $$$${that}\:{saying}\:'{contradiction}\:{found}' \\ $$$${makes}\:{sense}. \\ $$$$ \\ $$

Commented by Rasheed Soomro last updated on 01/Sep/15

$${Thankssssss}! \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com