Menu Close

lets-f-continuous-and-diferrenciable-f-x-1-xf-x-proof-that-n-N-0-f-n-x-1-nf-n-1-x-xf-n-x-where-f-n-x-d-n-f-dx-n-

Tinku Tara 0 Comments
Pin




Question Number 4100 by 123456 last updated on 28/Dec/15
lets f continuous and diferrenciable f(x+1)=xf(x) proof that n∈N/{0} f^((n)) (x+1)=nf^((n−1)) (x)+xf^((n)) (x) where f^((n)) (x)=(d^n f/dx^n )
$$\mathrm{lets}\:{f}\:\mathrm{continuous}\:\mathrm{and}\:\mathrm{diferrenciable} \\ $$$${f}\left({x}+\mathrm{1}\right)={xf}\left({x}\right) \\ $$$$\mathrm{proof}\:\mathrm{that}\:{n}\in\mathbb{N}/\left\{\mathrm{0}\right\} \\ $$$${f}^{\left({n}\right)} \left({x}+\mathrm{1}\right)={nf}^{\left({n}−\mathrm{1}\right)} \left({x}\right)+{xf}^{\left({n}\right)} \left({x}\right) \\ $$$$\mathrm{where} \\ $$$${f}^{\left({n}\right)} \left({x}\right)=\frac{{d}^{{n}} {f}}{{dx}^{{n}} } \\ $$
Answered by prakash jain last updated on 28/Dec/15
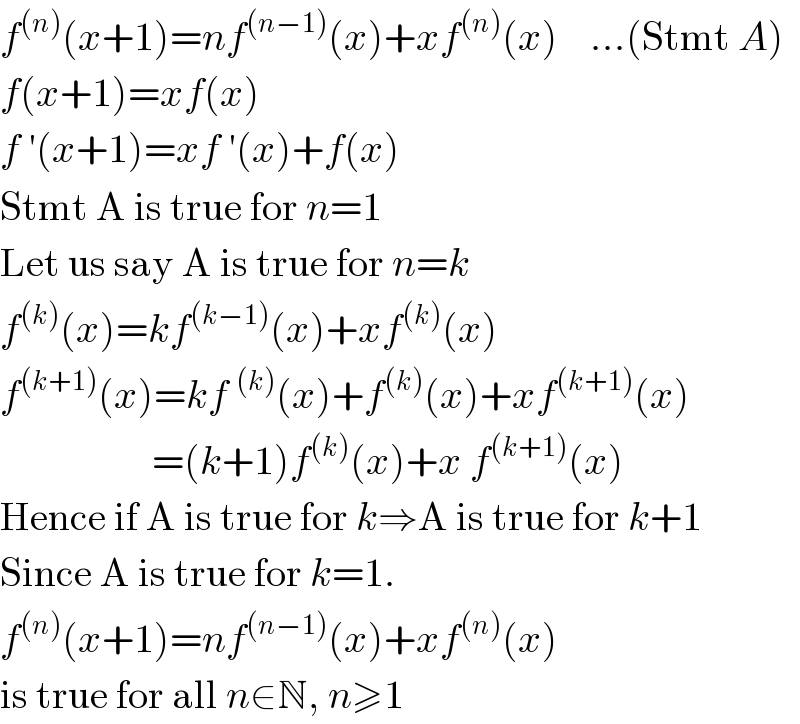
f^((n)) (x+1)=nf^((n−1)) (x)+xf^((n)) (x) ...(Stmt A) f(x+1)=xf(x) f ′(x+1)=xf ′(x)+f(x) Stmt A is true for n=1 Let us say A is true for n=k f^((k)) (x)=kf^((k−1)) (x)+xf^((k)) (x) f^((k+1)) (x)=kf^((k)) (x)+f^((k)) (x)+xf^((k+1)) (x) =(k+1)f^((k)) (x)+x f^((k+1)) (x) Hence if A is true for k⇒A is true for k+1 Since A is true for k=1. f^((n)) (x+1)=nf^((n−1)) (x)+xf^((n)) (x) is true for all n∈N, n≥1
$${f}^{\left({n}\right)} \left({x}+\mathrm{1}\right)={nf}^{\left({n}−\mathrm{1}\right)} \left({x}\right)+{xf}^{\left({n}\right)} \left({x}\right)\:\:\:\:…\left(\mathrm{Stmt}\:{A}\right) \\ $$$${f}\left({x}+\mathrm{1}\right)={xf}\left({x}\right) \\ $$$${f}\:'\left({x}+\mathrm{1}\right)={xf}\:'\left({x}\right)+{f}\left({x}\right) \\ $$$$\mathrm{Stmt}\:\mathrm{A}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:{n}=\mathrm{1} \\ $$$$\mathrm{Let}\:\mathrm{us}\:\mathrm{say}\:\mathrm{A}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:{n}={k} \\ $$$${f}^{\left({k}\right)} \left({x}\right)={kf}^{\left({k}−\mathrm{1}\right)} \left({x}\right)+{xf}^{\left({k}\right)} \left({x}\right) \\ $$$${f}^{\left({k}+\mathrm{1}\right)} \left({x}\right)={kf}\:^{\left({k}\right)} \left({x}\right)+{f}^{\left({k}\right)} \left({x}\right)+{xf}^{\left({k}+\mathrm{1}\right)} \left({x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({k}+\mathrm{1}\right){f}^{\left({k}\right)} \left({x}\right)+{x}\:{f}^{\left({k}+\mathrm{1}\right)} \left({x}\right) \\ $$$$\mathrm{Hence}\:\mathrm{if}\:\mathrm{A}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:{k}\Rightarrow\mathrm{A}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:{k}+\mathrm{1} \\ $$$$\mathrm{Since}\:\mathrm{A}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:{k}=\mathrm{1}. \\ $$$${f}^{\left({n}\right)} \left({x}+\mathrm{1}\right)={nf}^{\left({n}−\mathrm{1}\right)} \left({x}\right)+{xf}^{\left({n}\right)} \left({x}\right)\:\:\:\: \\ $$$$\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:{n}\in\mathbb{N},\:{n}\geqslant\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *