Question Number 746 by 123456 last updated on 06/Mar/15
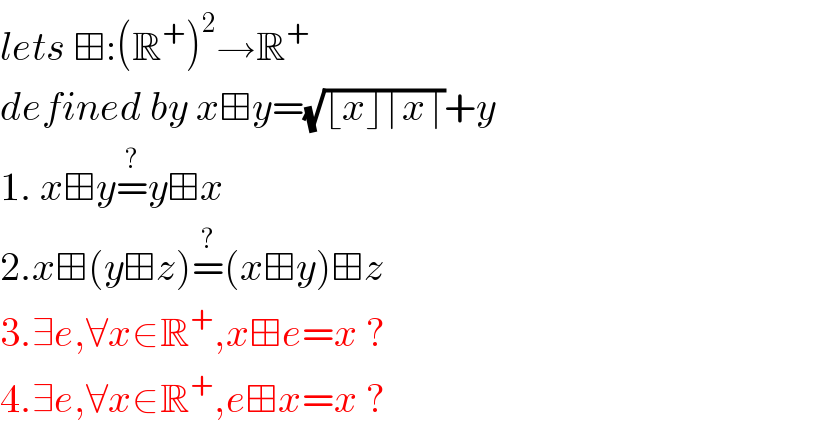
$${lets}\:\boxplus:\left(\mathbb{R}^{+} \right)^{\mathrm{2}} \rightarrow\mathbb{R}^{+} \\ $$$${defined}\:{by}\:{x}\boxplus{y}=\sqrt{\lfloor{x}\rfloor\lceil{x}\rceil}+{y} \\ $$$$\mathrm{1}.\:{x}\boxplus{y}\overset{?} {=}{y}\boxplus{x} \\ $$$$\mathrm{2}.{x}\boxplus\left({y}\boxplus{z}\right)\overset{?} {=}\left({x}\boxplus{y}\right)\boxplus{z} \\ $$$$\mathrm{3}.\exists{e},\forall{x}\in\mathbb{R}^{+} ,{x}\boxplus{e}={x}\:? \\ $$$$\mathrm{4}.\exists{e},\forall{x}\in\mathbb{R}^{+} ,{e}\boxplus{x}={x}\:? \\ $$
Commented by prakash jain last updated on 06/Mar/15

$$\mathrm{1}.\:{y}=\mathrm{5},\:{x}=\mathrm{4}.\mathrm{5} \\ $$$${x}\boxplus{y}=\sqrt{\mathrm{4}×\mathrm{5}}+\mathrm{5}=\mathrm{5}+\sqrt{\mathrm{20}} \\ $$$${y}\boxplus{x}=\mathrm{10} \\ $$$${x}\boxplus{y}\neq{y}\boxplus{x} \\ $$$$\mathrm{2}.\:{x}=\mathrm{4}.\mathrm{5},\:{y}=\mathrm{5}.\mathrm{5},\:{z}=\mathrm{6} \\ $$$${x}\boxplus\left({y}\boxplus{z}\right)\neq\left({x}\boxplus{y}\right)\boxplus{z} \\ $$
Answered by prakash jain last updated on 06/Mar/15

$$\sqrt{\lfloor{x}\rfloor\lceil{x}\rceil} \\ $$$$\lfloor{x}\rfloor={x}−{a}\:\:\:{where}\:{a}=\left\{{x}\right\}={fractional}\:{part} \\ $$$$\lceil{x}\rceil={x}+\mathrm{1}−{a} \\ $$$$\left({x}−{a}\right)\left({x}+\mathrm{1}−{a}\right)={x}^{\mathrm{2}} −{ax}+{x}−{a}−{ax}+{a}^{\mathrm{2}} \\ $$$$={x}^{\mathrm{2}} −\mathrm{2}{ax}+{a}^{\mathrm{2}} +{x}−{a} \\ $$$${y}={a}^{\mathrm{2}} −\mathrm{2}{ax}+{x}−{a}=\left({a}^{\mathrm{2}} −{a}\right)+{x}\left(\mathrm{1}−\mathrm{2}{a}\right)<\mathrm{0}\:\mathrm{for}\:{a}>\mathrm{0}.\mathrm{5} \\ $$$$\mathrm{So}\:\forall{x}\mid\left\{{x}\right\}>.\mathrm{5}\:\nexists{e}\in\mathbb{R}^{+} ,{x}\boxplus\mathrm{e}={x} \\ $$$$\mathrm{Statment}\:\mathrm{3}\:\mathrm{is}\:\mathrm{false}. \\ $$$$\mathrm{4}.\:{e}=\mathrm{0} \\ $$$$\mathrm{0}\boxplus{x}={x} \\ $$
