Question Number 1251 by 123456 last updated on 18/Jul/15
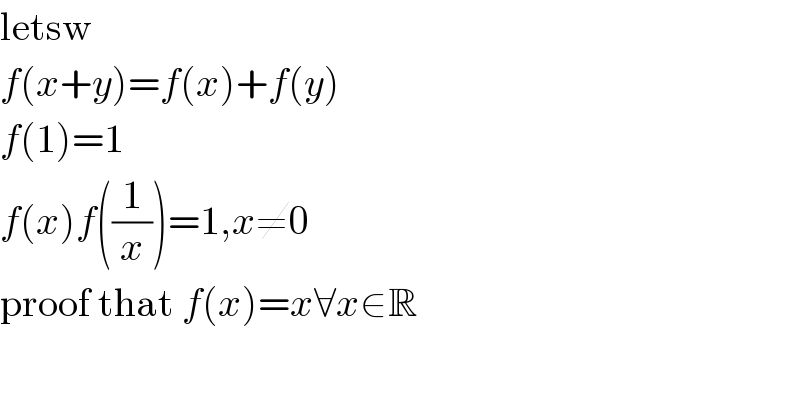
$$\mathrm{letsw} \\ $$$${f}\left({x}+{y}\right)={f}\left({x}\right)+{f}\left({y}\right) \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$${f}\left({x}\right){f}\left(\frac{\mathrm{1}}{{x}}\right)=\mathrm{1},{x}\neq\mathrm{0} \\ $$$$\mathrm{proof}\:\mathrm{that}\:{f}\left({x}\right)={x}\forall{x}\in\mathbb{R} \\ $$
Commented by prakash jain last updated on 18/Jul/15
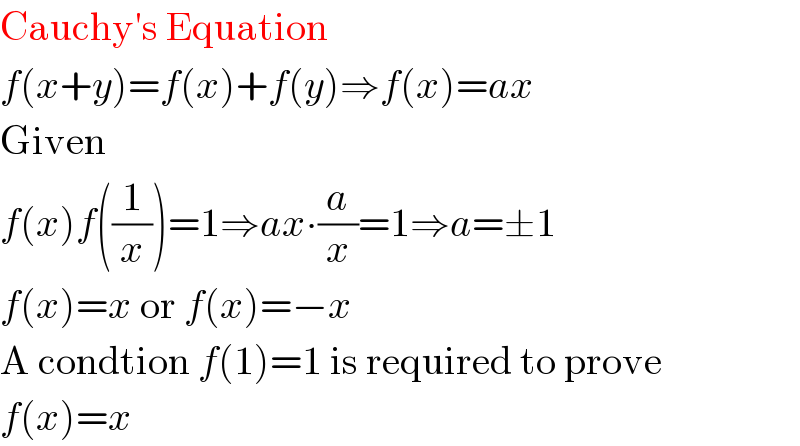
$$\mathrm{Cauchy}'\mathrm{s}\:\mathrm{Equation} \\ $$$${f}\left({x}+{y}\right)={f}\left({x}\right)+{f}\left({y}\right)\Rightarrow{f}\left({x}\right)={ax} \\ $$$$\mathrm{Given} \\ $$$${f}\left({x}\right){f}\left(\frac{\mathrm{1}}{{x}}\right)=\mathrm{1}\Rightarrow{ax}\centerdot\frac{{a}}{{x}}=\mathrm{1}\Rightarrow{a}=\pm\mathrm{1} \\ $$$${f}\left({x}\right)={x}\:\mathrm{or}\:{f}\left({x}\right)=−{x} \\ $$$$\mathrm{A}\:\mathrm{condtion}\:{f}\left(\mathrm{1}\right)=\mathrm{1}\:\mathrm{is}\:\mathrm{required}\:\mathrm{to}\:\mathrm{prove} \\ $$$${f}\left({x}\right)={x} \\ $$
