Question Number 73223 by malwaan last updated on 08/Nov/19

$$\boldsymbol{{lim}}\:\frac{\mathrm{0}}{\infty}\:\overset{?} {=}\:\mathrm{0}\:? \\ $$$$\boldsymbol{{lim}}\:\frac{\infty}{\mathrm{0}}\:\overset{?} {=}\:\infty\:? \\ $$
Commented by MJS last updated on 08/Nov/19
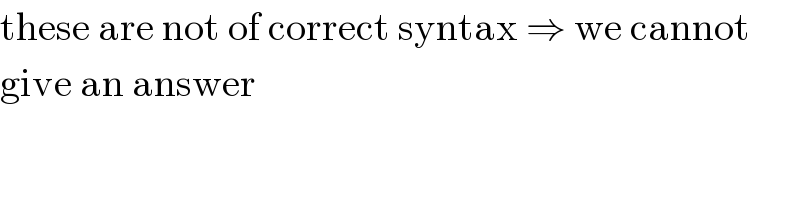
$$\mathrm{these}\:\mathrm{are}\:\mathrm{not}\:\mathrm{of}\:\mathrm{correct}\:\mathrm{syntax}\:\Rightarrow\:\mathrm{we}\:\mathrm{cannot} \\ $$$$\mathrm{give}\:\mathrm{an}\:\mathrm{answer} \\ $$
Commented by malwaan last updated on 09/Nov/19

$${A}\:{student}\:{asked}\:{me}\:{this}\:{question} \\ $$$${I}\:{answered} \\ $$$$\boldsymbol{{lim}}\frac{\mathrm{0}}{\infty}\:=\:\boldsymbol{{lim}}\:\mathrm{0}×\boldsymbol{{lim}}\frac{\mathrm{1}}{\infty}=\mathrm{0}×\mathrm{0}=\mathrm{0} \\ $$$$\boldsymbol{{also}}\:\frac{\infty}{\mathrm{0}}\:=\:\infty×\frac{\mathrm{1}}{\mathrm{0}}\:=\:\infty×\infty\:=\:\infty \\ $$$$\boldsymbol{{Am}}\:\boldsymbol{{I}}\:\boldsymbol{{right}}\:??? \\ $$$$ \\ $$
Commented by malwaan last updated on 09/Nov/19

$${example} \\ $$$$\underset{\boldsymbol{{x}}\rightarrow\frac{\pi}{\mathrm{2}}} {\boldsymbol{{lim}}}\:\:\:\frac{\boldsymbol{{tan}}\:\boldsymbol{{x}}}{\boldsymbol{{x}}−\frac{\boldsymbol{\pi}}{\mathrm{2}}}\:\:=\:\frac{\pm\infty}{\mathrm{0}}\:=\pm\infty×\infty \\ $$$$\overset{?} {=}\:\pm\infty \\ $$
Commented by malwaan last updated on 10/Nov/19

$${sorry}\:{sir}\:{mjs} \\ $$$${and}\:{thanks}\: \\ $$
Commented by malwaan last updated on 11/Nov/19

$$\underset{{x}\rightarrow\left(\frac{\pi}{\mathrm{2}}\right)^{+} } {{lim}_{} }\:=\:\frac{−}{+}\:=\:−\infty \\ $$$$\underset{{x}\rightarrow\left(\frac{\pi}{\mathrm{2}}\right)^{−} } {{lim}}\:\:=\:\frac{+}{−}\:=\:−\infty \\ $$$$\boldsymbol{{SO}}\:\boldsymbol{{THE}}\:\boldsymbol{{LIMIT}}\:\boldsymbol{{EXIST}} \\ $$$$\boldsymbol{{AND}}\:\boldsymbol{{EQUALS}}\:\boldsymbol{{TO}}\:−\infty \\ $$
