Question Number 131079 by mathlove last updated on 01/Feb/21
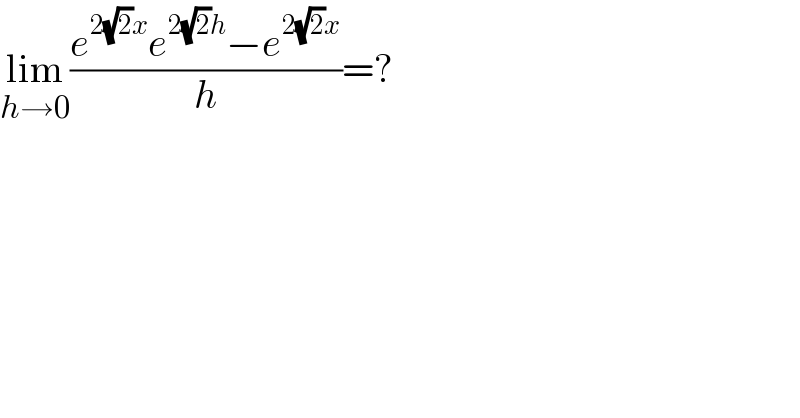
$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\mathrm{2}\sqrt{\mathrm{2}}{x}} {e}^{\mathrm{2}\sqrt{\mathrm{2}}{h}} −{e}^{\mathrm{2}\sqrt{\mathrm{2}}{x}} }{{h}}=? \\ $$
Commented by EDWIN88 last updated on 01/Feb/21
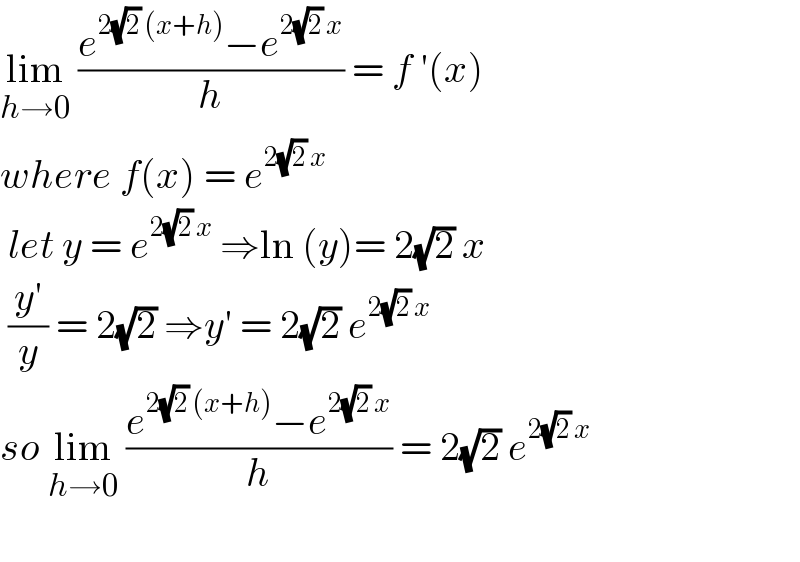
$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{e}^{\mathrm{2}\sqrt{\mathrm{2}}\:\left({x}+{h}\right)} −{e}^{\mathrm{2}\sqrt{\mathrm{2}}\:{x}} }{{h}}\:=\:{f}\:'\left({x}\right) \\ $$$${where}\:{f}\left({x}\right)\:=\:{e}^{\mathrm{2}\sqrt{\mathrm{2}}\:{x}} \\ $$$$\:{let}\:{y}\:=\:{e}^{\mathrm{2}\sqrt{\mathrm{2}}\:{x}} \:\Rightarrow\mathrm{ln}\:\left({y}\right)=\:\mathrm{2}\sqrt{\mathrm{2}}\:{x} \\ $$$$\:\frac{{y}'}{{y}}\:=\:\mathrm{2}\sqrt{\mathrm{2}}\:\Rightarrow{y}'\:=\:\mathrm{2}\sqrt{\mathrm{2}}\:{e}^{\mathrm{2}\sqrt{\mathrm{2}}\:{x}} \\ $$$${so}\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{e}^{\mathrm{2}\sqrt{\mathrm{2}}\:\left({x}+{h}\right)} −{e}^{\mathrm{2}\sqrt{\mathrm{2}}\:{x}} }{{h}}\:=\:\mathrm{2}\sqrt{\mathrm{2}}\:{e}^{\mathrm{2}\sqrt{\mathrm{2}}\:{x}} \\ $$$$ \\ $$
Answered by EDWIN88 last updated on 01/Feb/21
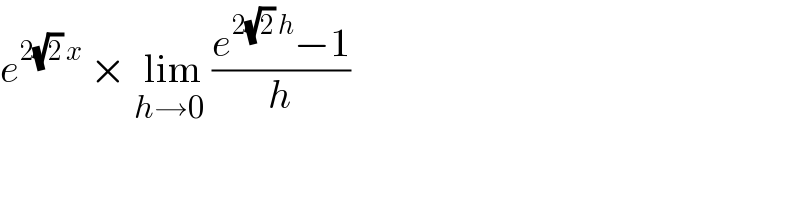
$${e}^{\mathrm{2}\sqrt{\mathrm{2}}\:{x}} \:×\:\underset{{h}\rightarrow\mathrm{0}\:} {\mathrm{lim}}\frac{{e}^{\mathrm{2}\sqrt{\mathrm{2}}\:{h}} −\mathrm{1}}{{h}} \\ $$
Commented by mathlove last updated on 01/Feb/21

$${and} \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\mathrm{2}\sqrt{\mathrm{2}}{h}} −\mathrm{1}}{{h}}=? \\ $$
Commented by Dwaipayan Shikari last updated on 01/Feb/21
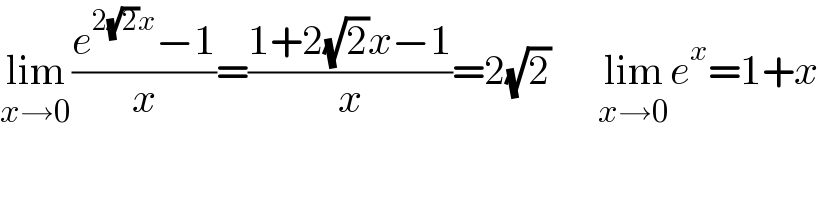
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\mathrm{2}\sqrt{\mathrm{2}}{x}} −\mathrm{1}}{{x}}=\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}{x}−\mathrm{1}}{{x}}=\mathrm{2}\sqrt{\mathrm{2}}\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{e}^{{x}} =\mathrm{1}+{x} \\ $$
