Question Number 138801 by mnjuly1970 last updated on 18/Apr/21
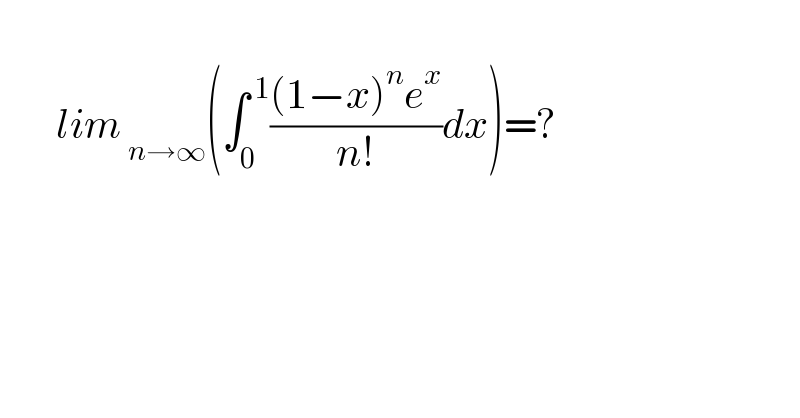
$$\: \\ $$$$\:\:\:\:\:\:\:{lim}_{\:{n}\rightarrow\infty} \left(\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{1}−{x}\right)^{{n}} {e}^{{x}} }{{n}!}{dx}\right)=? \\ $$
Answered by Kamel last updated on 18/Apr/21

Commented by mnjuly1970 last updated on 18/Apr/21
$${thanks}\:{mr}\:{kamel}\: \\ $$$${very}\:{nice}… \\ $$
Answered by mr W last updated on 18/Apr/21
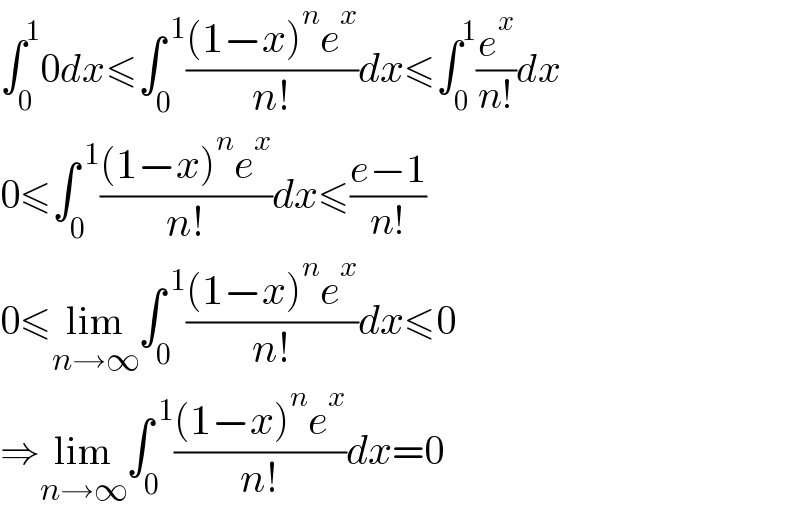
$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{0}{dx}\leqslant\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{1}−{x}\right)^{{n}} {e}^{{x}} }{{n}!}{dx}\leqslant\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{e}^{{x}} }{{n}!}{dx} \\ $$$$\mathrm{0}\leqslant\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{1}−{x}\right)^{{n}} {e}^{{x}} }{{n}!}{dx}\leqslant\frac{{e}−\mathrm{1}}{{n}!} \\ $$$$\mathrm{0}\leqslant\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{1}−{x}\right)^{{n}} {e}^{{x}} }{{n}!}{dx}\leqslant\mathrm{0} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{1}−{x}\right)^{{n}} {e}^{{x}} }{{n}!}{dx}=\mathrm{0} \\ $$
Commented by mnjuly1970 last updated on 18/Apr/21
$${grateful}\:{mr}\:{W}… \\ $$
