Question Number 143156 by mohammad17 last updated on 10/Jun/21
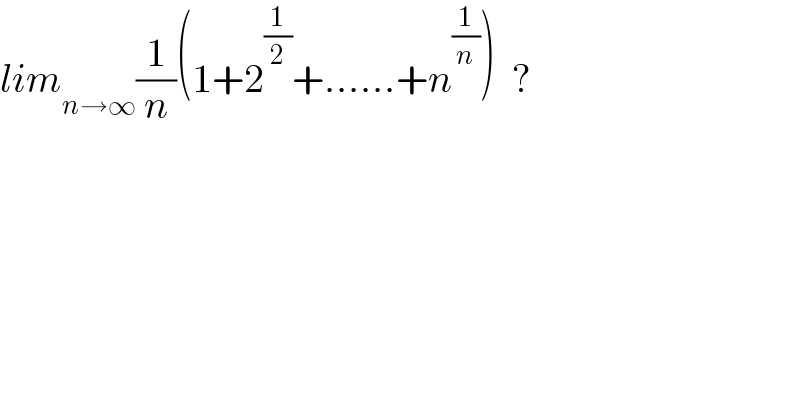
$${lim}_{{n}\rightarrow\infty} \frac{\mathrm{1}}{{n}}\left(\mathrm{1}+\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} +……+{n}^{\frac{\mathrm{1}}{{n}}} \right)\:\:? \\ $$
Answered by mr W last updated on 10/Jun/21
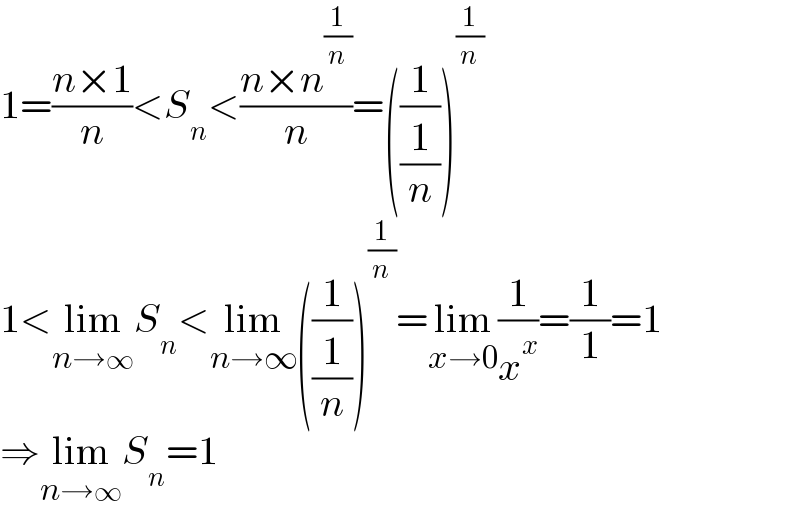
$$\mathrm{1}=\frac{{n}×\mathrm{1}}{{n}}<{S}_{{n}} <\frac{{n}×{n}^{\frac{\mathrm{1}}{{n}}} }{{n}}=\left(\frac{\mathrm{1}}{\frac{\mathrm{1}}{{n}}}\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$$\mathrm{1}<\underset{{n}\rightarrow\infty} {\mathrm{lim}}{S}_{{n}} <\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\frac{\mathrm{1}}{{n}}}\right)^{\frac{\mathrm{1}}{{n}}} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}^{{x}} }=\frac{\mathrm{1}}{\mathrm{1}}=\mathrm{1} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}{S}_{{n}} =\mathrm{1} \\ $$
