Question Number 75468 by aliesam last updated on 11/Dec/19
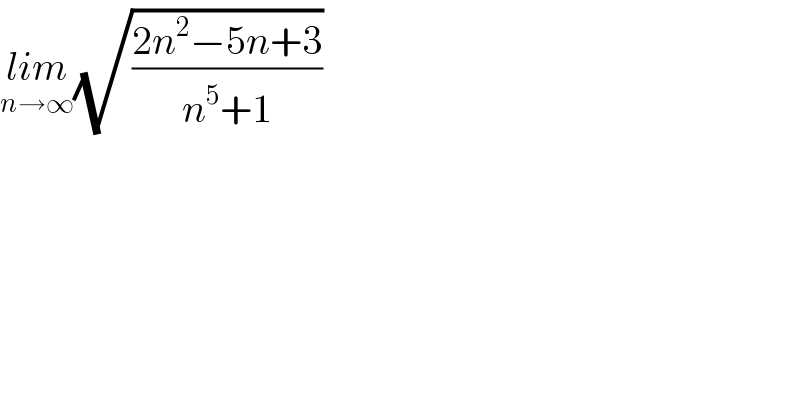
$$\underset{{n}\rightarrow\infty} {{lim}}\sqrt{\frac{\mathrm{2}{n}^{\mathrm{2}} −\mathrm{5}{n}+\mathrm{3}}{{n}^{\mathrm{5}} +\mathrm{1}}} \\ $$
Commented by MJS last updated on 11/Dec/19
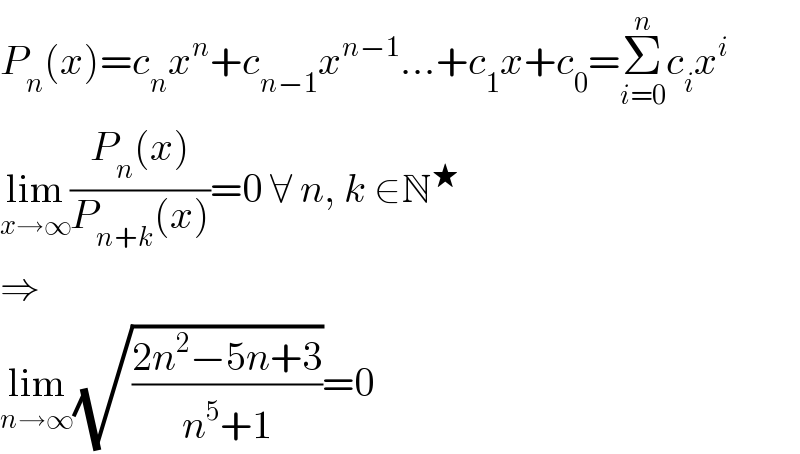
$${P}_{{n}} \left({x}\right)={c}_{{n}} {x}^{{n}} +{c}_{{n}−\mathrm{1}} {x}^{{n}−\mathrm{1}} …+{c}_{\mathrm{1}} {x}+{c}_{\mathrm{0}} =\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{c}_{{i}} {x}^{{i}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{P}_{{n}} \left({x}\right)}{{P}_{{n}+{k}} \left({x}\right)}=\mathrm{0}\:\forall\:{n},\:{k}\:\in\mathbb{N}^{\bigstar} \\ $$$$\Rightarrow \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\sqrt{\frac{\mathrm{2}{n}^{\mathrm{2}} −\mathrm{5}{n}+\mathrm{3}}{{n}^{\mathrm{5}} +\mathrm{1}}}=\mathrm{0} \\ $$
Commented by mathmax by abdo last updated on 12/Dec/19
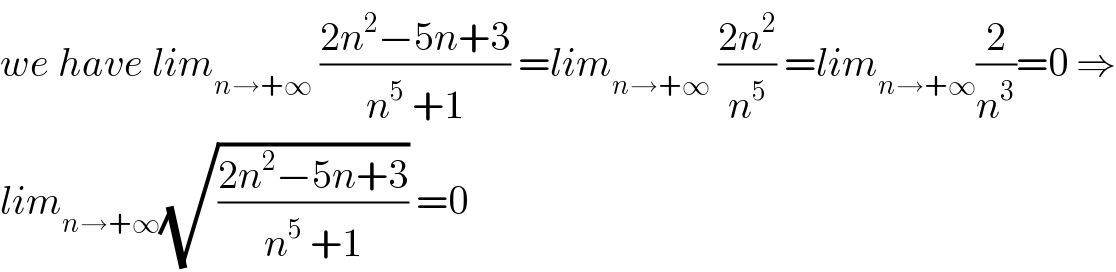
$${we}\:{have}\:{lim}_{{n}\rightarrow+\infty} \:\frac{\mathrm{2}{n}^{\mathrm{2}} −\mathrm{5}{n}+\mathrm{3}}{{n}^{\mathrm{5}} \:+\mathrm{1}}\:={lim}_{{n}\rightarrow+\infty} \:\frac{\mathrm{2}{n}^{\mathrm{2}} }{{n}^{\mathrm{5}} }\:={lim}_{{n}\rightarrow+\infty} \frac{\mathrm{2}}{{n}^{\mathrm{3}} }=\mathrm{0}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \sqrt{\frac{\mathrm{2}{n}^{\mathrm{2}} −\mathrm{5}{n}+\mathrm{3}}{{n}^{\mathrm{5}} \:+\mathrm{1}}}\:=\mathrm{0} \\ $$
