lim-n-2n-n-n-n-1-n-

Question Number 142464 by som(math1967) last updated on 01/Jun/21

$$\underset{\boldsymbol{{n}}\rightarrow\infty} {\boldsymbol{{lim}}}\:\left[\frac{\left(\mathrm{2}\boldsymbol{{n}}\right)!}{\boldsymbol{{n}}!\boldsymbol{{n}}^{\boldsymbol{{n}}} }\right]^{\frac{\mathrm{1}}{\boldsymbol{{n}}}} =? \\ $$

Answered by Dwaipayan Shikari last updated on 01/Jun/21

lim_(n→∞) [((2^(2n) n^(2n) e^(−2n) (√(4πn)))/(n^n e^(−n) (√(2πn)) n^n ))]^(1/n) =y ⇒[((4/e))^n (√2)]^(1/n) =y⇒y=(4/e)

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{\mathrm{2}^{\mathrm{2}{n}} {n}^{\mathrm{2}{n}} {e}^{−\mathrm{2}{n}} \sqrt{\mathrm{4}\pi{n}}}{{n}^{{n}} {e}^{−{n}} \sqrt{\mathrm{2}\pi{n}}\:{n}^{{n}} }\right]^{\frac{\mathrm{1}}{{n}}} ={y} \\ $$$$\Rightarrow\left[\left(\frac{\mathrm{4}}{{e}}\right)^{{n}} \sqrt{\mathrm{2}}\right]^{\frac{\mathrm{1}}{{n}}} ={y}\Rightarrow{y}=\frac{\mathrm{4}}{{e}} \\ $$

Answered by Dwaipayan Shikari last updated on 01/Jun/21

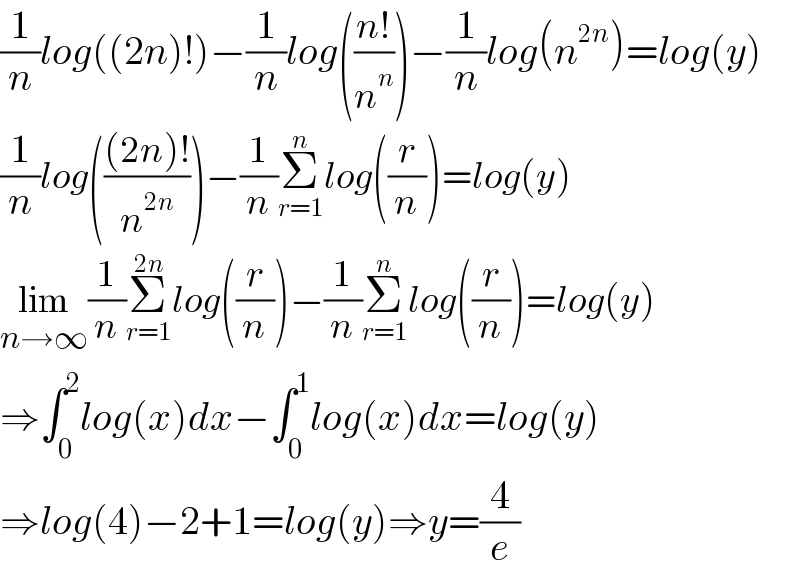
(1/n)log((2n)!)−(1/n)log(((n!)/n^n ))−(1/n)log(n^(2n) )=log(y) (1/n)log((((2n)!)/n^(2n) ))−(1/n)Σ_(r=1) ^n log((r/n))=log(y) lim_(n→∞) (1/n)Σ_(r=1) ^(2n) log((r/n))−(1/n)Σ_(r=1) ^n log((r/n))=log(y) ⇒∫_0 ^2 log(x)dx−∫_0 ^1 log(x)dx=log(y) ⇒log(4)−2+1=log(y)⇒y=(4/e)

$$\frac{\mathrm{1}}{{n}}{log}\left(\left(\mathrm{2}{n}\right)!\right)−\frac{\mathrm{1}}{{n}}{log}\left(\frac{{n}!}{{n}^{{n}} }\right)−\frac{\mathrm{1}}{{n}}{log}\left({n}^{\mathrm{2}{n}} \right)={log}\left({y}\right) \\ $$$$\frac{\mathrm{1}}{{n}}{log}\left(\frac{\left(\mathrm{2}{n}\right)!}{{n}^{\mathrm{2}{n}} }\right)−\frac{\mathrm{1}}{{n}}\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{log}\left(\frac{{r}}{{n}}\right)={log}\left({y}\right) \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{r}=\mathrm{1}} {\overset{\mathrm{2}{n}} {\sum}}{log}\left(\frac{{r}}{{n}}\right)−\frac{\mathrm{1}}{{n}}\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{log}\left(\frac{{r}}{{n}}\right)={log}\left({y}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{2}} {log}\left({x}\right){dx}−\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left({x}\right){dx}={log}\left({y}\right) \\ $$$$\Rightarrow{log}\left(\mathrm{4}\right)−\mathrm{2}+\mathrm{1}={log}\left({y}\right)\Rightarrow{y}=\frac{\mathrm{4}}{{e}} \\ $$

Commented by som(math1967) last updated on 01/Jun/21

$$\boldsymbol{{Thank}}\:\boldsymbol{{you}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply