Question Number 75469 by aliesam last updated on 11/Dec/19
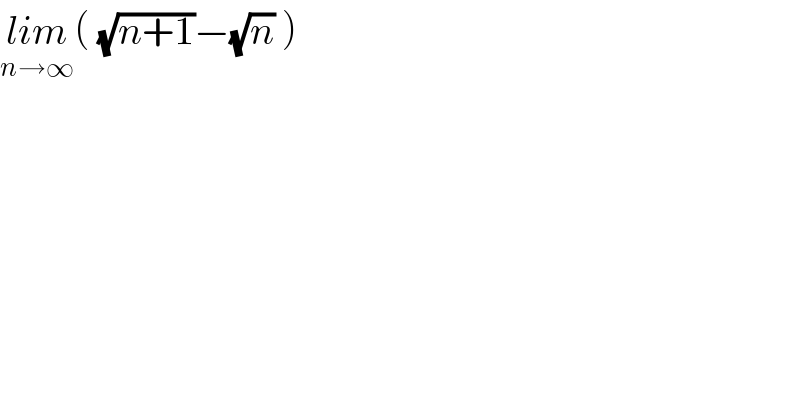
$$\underset{{n}\rightarrow\infty} {{lim}}\left(\:\sqrt{{n}+\mathrm{1}}−\sqrt{{n}}\:\right) \\ $$
Commented by MJS last updated on 11/Dec/19
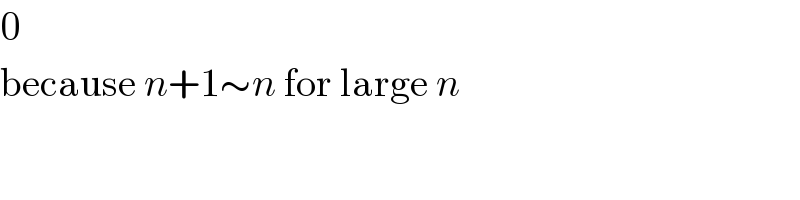
$$\mathrm{0} \\ $$$$\mathrm{because}\:{n}+\mathrm{1}\sim{n}\:\mathrm{for}\:\mathrm{large}\:{n} \\ $$
Commented by mathmax by abdo last updated on 12/Dec/19
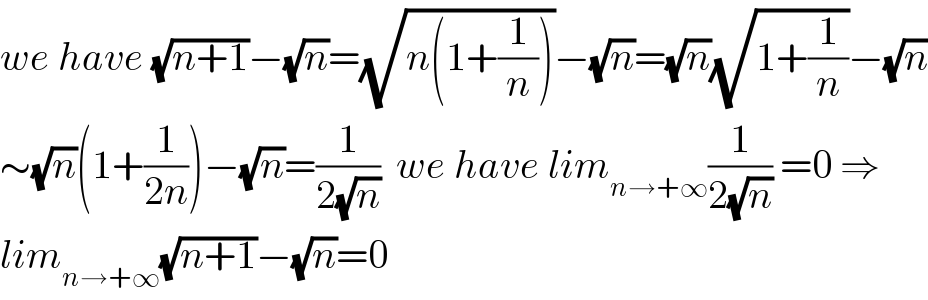
$${we}\:{have}\:\sqrt{{n}+\mathrm{1}}−\sqrt{{n}}=\sqrt{{n}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)}−\sqrt{{n}}=\sqrt{{n}}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{n}}}−\sqrt{{n}} \\ $$$$\sim\sqrt{{n}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right)−\sqrt{{n}}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{n}}}\:\:{we}\:{have}\:{lim}_{{n}\rightarrow+\infty} \frac{\mathrm{1}}{\mathrm{2}\sqrt{{n}}}\:=\mathrm{0}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \sqrt{{n}+\mathrm{1}}−\sqrt{{n}}=\mathrm{0} \\ $$
