Question Number 71777 by Henri Boucatchou last updated on 19/Oct/19
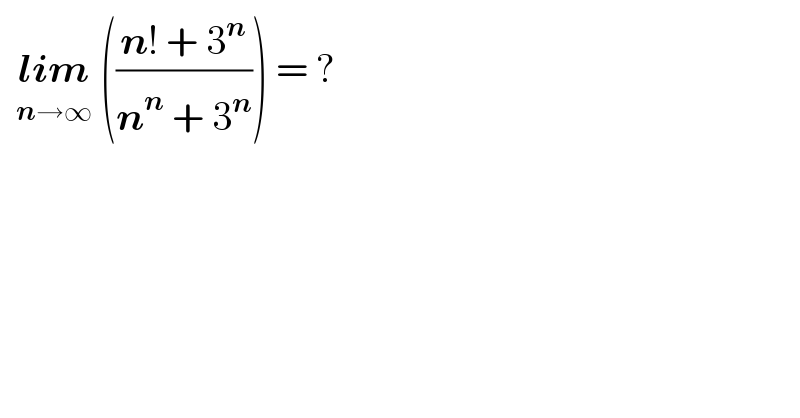
$$\:\:\underset{\boldsymbol{{n}}\rightarrow\infty} {\boldsymbol{{lim}}}\:\left(\frac{\boldsymbol{{n}}!\:+\:\mathrm{3}^{\boldsymbol{{n}}} }{\boldsymbol{{n}}^{\boldsymbol{{n}}} \:+\:\mathrm{3}^{\boldsymbol{{n}}} }\right)\:=\:? \\ $$
Commented by mathmax by abdo last updated on 19/Oct/19

$${let}\:{A}_{{n}} =\frac{{n}!\:+\mathrm{3}^{{n}} }{{n}^{{n}} \:+\mathrm{3}^{{n}} }\:\:\:{we}\:{have}\:\:{n}!\sim{n}^{{n}} {e}^{−{n}} \sqrt{\mathrm{2}\pi{n}}\left({stirling}\right)\:\Rightarrow \\ $$$${A}_{{n}} \sim\:\frac{{n}^{{n}} \:{e}^{−{n}} \sqrt{\mathrm{2}\pi{n}}+\mathrm{3}^{{n}} }{{n}^{{n}} \:+\mathrm{3}^{{n}} }\:=\frac{{n}^{{n}} \left\{\:{e}^{−{n}} \sqrt{\mathrm{2}\pi{n}}+\left(\frac{\mathrm{3}}{{n}}\right)^{{n}} \right\}}{{n}^{{n}} \left(\mathrm{1}+\left(\frac{\mathrm{3}}{{n}}\right)^{{n}} \right)} \\ $$$$=\frac{{e}^{−{n}} \sqrt{\mathrm{2}\pi{n}}+\left(\frac{\mathrm{3}}{{n}}\right)^{{n}} }{\mathrm{1}+\left(\frac{\mathrm{3}}{{n}}\right)^{{n}} }\: \\ $$$$\:{we}\:{have}\:{lim}_{{n}\rightarrow+\infty} \:{e}^{−{n}} \sqrt{\mathrm{2}\pi{n}}\:=\mathrm{0}\:{and}\:\:\left(\frac{\mathrm{3}}{{n}}\right)^{{n}} ={e}^{{nln}\left(\frac{\mathrm{3}}{{n}}\right)} \\ $$$${we}\:{use}\:{the}\:{changement}\:\frac{\mathrm{3}}{{n}}\:={t}\:\:\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \left(\frac{\mathrm{3}}{{n}}\right)^{{n}} ={lim}_{{t}\rightarrow\mathrm{0}} \:{e}^{\frac{\mathrm{3}}{{t}}{ln}\left({t}\right)} \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}^{+} } \:\:\:{e}^{\frac{\mathrm{3}{tln}\left({t}\right)}{{t}^{\mathrm{2}} }} \:\:=\mathrm{0}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} =\mathrm{0} \\ $$
