Question Number 142668 by mathdanisur last updated on 03/Jun/21
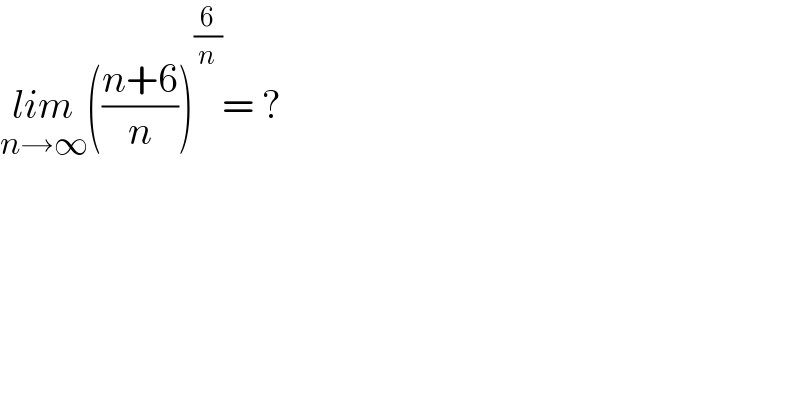
$$\underset{{n}\rightarrow\infty} {{lim}}\left(\frac{{n}+\mathrm{6}}{{n}}\right)^{\frac{\mathrm{6}}{{n}}} =\:? \\ $$
Commented by iloveisrael last updated on 04/Jun/21
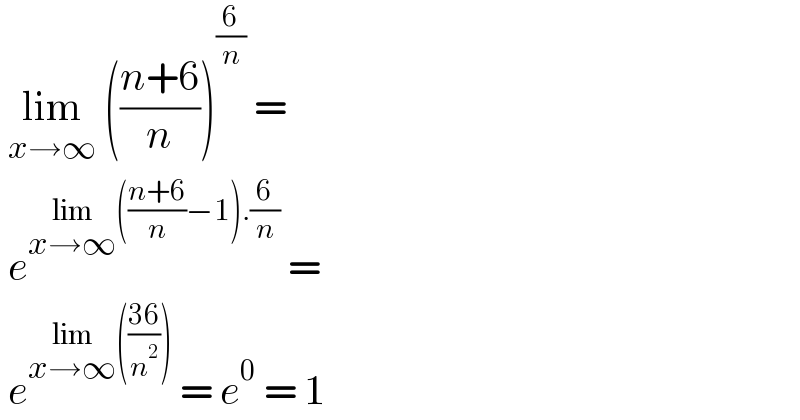
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{{n}+\mathrm{6}}{{n}}\right)^{\frac{\mathrm{6}}{{n}}} \:= \\ $$$$\:{e}^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{n}+\mathrm{6}}{{n}}−\mathrm{1}\right).\frac{\mathrm{6}}{{n}}} \:= \\ $$$$\:{e}^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{36}}{{n}^{\mathrm{2}} }\right)} \:=\:{e}^{\mathrm{0}} \:=\:\mathrm{1} \\ $$
Commented by mathdanisur last updated on 05/Jun/21

$${thanks}\:{sir} \\ $$
Answered by ajfour last updated on 03/Jun/21
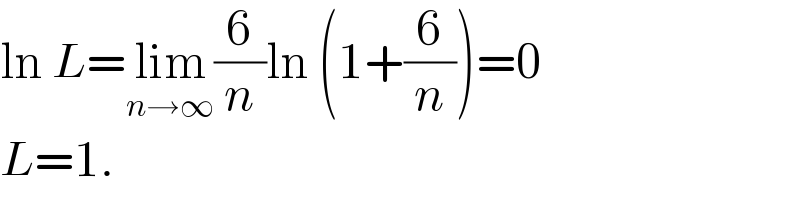
$$\mathrm{ln}\:{L}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{6}}{{n}}\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{6}}{{n}}\right)=\mathrm{0} \\ $$$${L}=\mathrm{1}. \\ $$
Answered by Ankushkumarparcha last updated on 03/Jun/21

$${Answer}:\:{e} \\ $$
Answered by mr W last updated on 03/Jun/21
![lim_(n→∞) (((n+6)/n))^(6/n) =lim_(n→∞) [(1+(1/(n/6)))^(n/6) ]^((36)/n^2 ) =e^0 =1](https://www.tinkutara.com/question/Q142673.png)
$$\underset{{n}\rightarrow\infty} {{lim}}\left(\frac{{n}+\mathrm{6}}{{n}}\right)^{\frac{\mathrm{6}}{{n}}} \\ $$$$=\underset{{n}\rightarrow\infty} {{lim}}\left[\left(\mathrm{1}+\frac{\mathrm{1}}{\frac{{n}}{\mathrm{6}}}\right)^{\frac{{n}}{\mathrm{6}}} \right]^{\frac{\mathrm{36}}{{n}^{\mathrm{2}} }} \\ $$$$={e}^{\mathrm{0}} =\mathrm{1} \\ $$
Commented by mathdanisur last updated on 05/Jun/21

$${thanks}\:{sir} \\ $$
