lim-n-S-i-1-n-i-n-1-L-S-R-S-gt-0-What-can-we-tell-about-L-Does-there-exist-a-limit-Is-it-positive-negative-

Question Number 5207 by FilupSmith last updated on 30/Apr/16

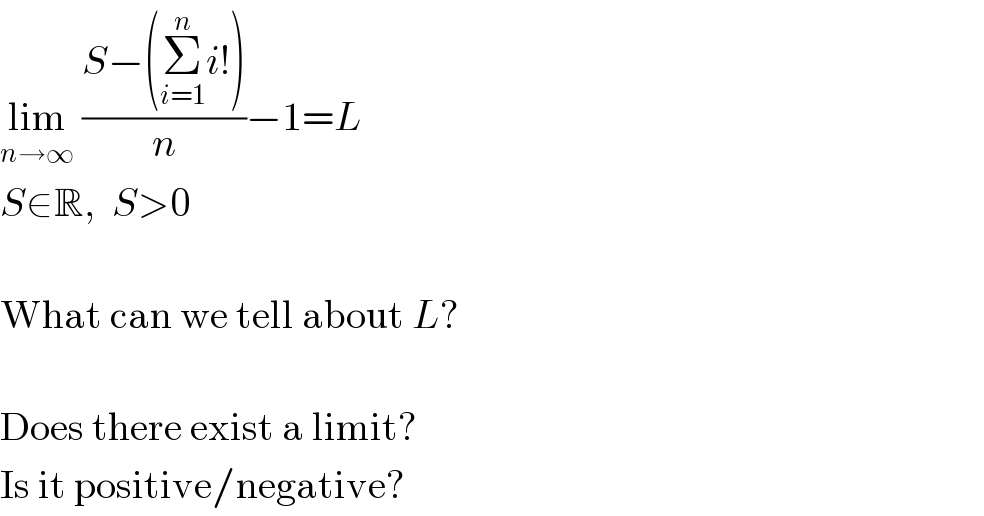
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{S}−\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{i}!\right)}{{n}}−\mathrm{1}={L} \\ $$$${S}\in\mathbb{R},\:\:{S}>\mathrm{0} \\ $$$$ \\ $$$$\mathrm{What}\:\mathrm{can}\:\mathrm{we}\:\mathrm{tell}\:\mathrm{about}\:{L}? \\ $$$$ \\ $$$$\mathrm{Does}\:\mathrm{there}\:\mathrm{exist}\:\mathrm{a}\:\mathrm{limit}? \\ $$$$\mathrm{Is}\:\mathrm{it}\:\mathrm{positive}/\mathrm{negative}? \\ $$

Commented by FilupSmith last updated on 30/Apr/16

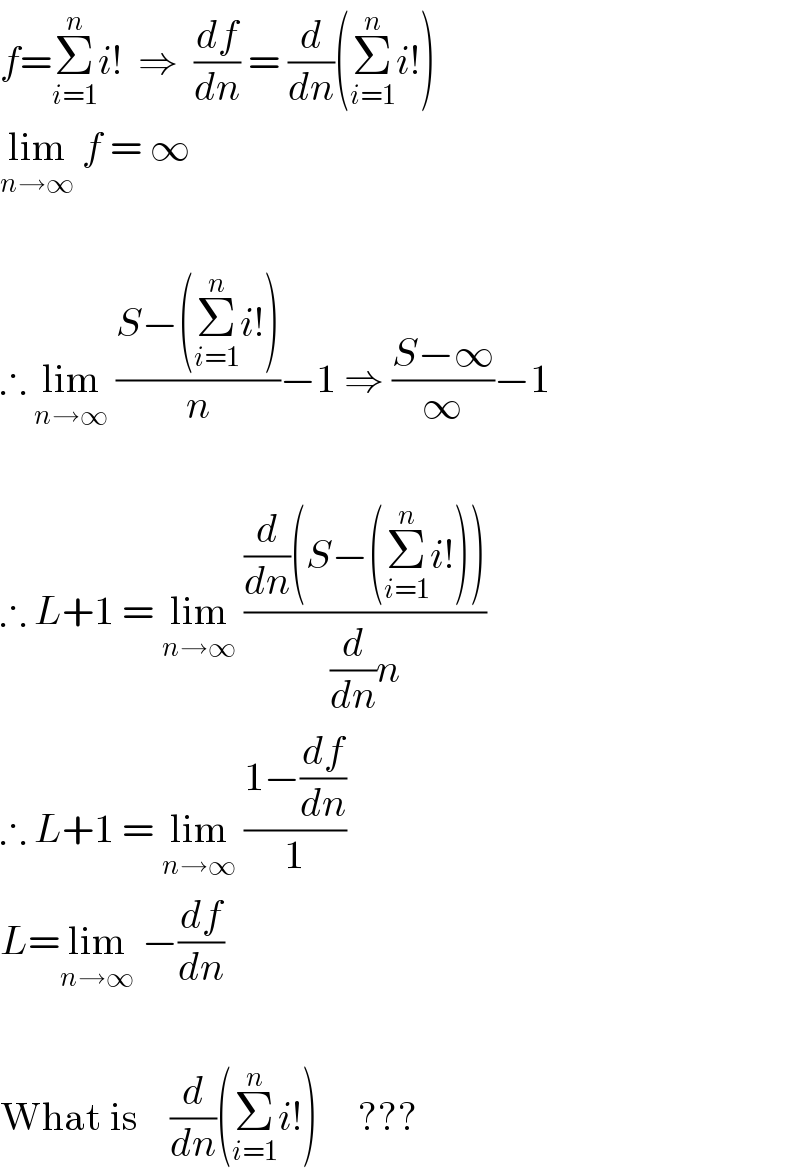
$${f}=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{i}!\:\:\Rightarrow\:\:\frac{{df}}{{dn}}\:=\:\frac{{d}}{{dn}}\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{i}!\right) \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{f}\:=\:\infty \\ $$$$ \\ $$$$\therefore\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{S}−\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{i}!\right)}{{n}}−\mathrm{1}\:\Rightarrow\:\frac{{S}−\infty}{\infty}−\mathrm{1} \\ $$$$ \\ $$$$\therefore\:{L}+\mathrm{1}\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\frac{{d}}{{dn}}\left({S}−\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{i}!\right)\right)}{\frac{{d}}{{dn}}{n}} \\ $$$$\therefore\:{L}+\mathrm{1}\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}−\frac{{df}}{{dn}}}{\mathrm{1}} \\ $$$${L}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:−\frac{{df}}{{dn}} \\ $$$$ \\ $$$$\mathrm{What}\:\mathrm{is}\:\:\:\:\frac{{d}}{{dn}}\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{i}!\right)\:\:\:\:\:??? \\ $$

Commented by FilupSmith last updated on 30/Apr/16

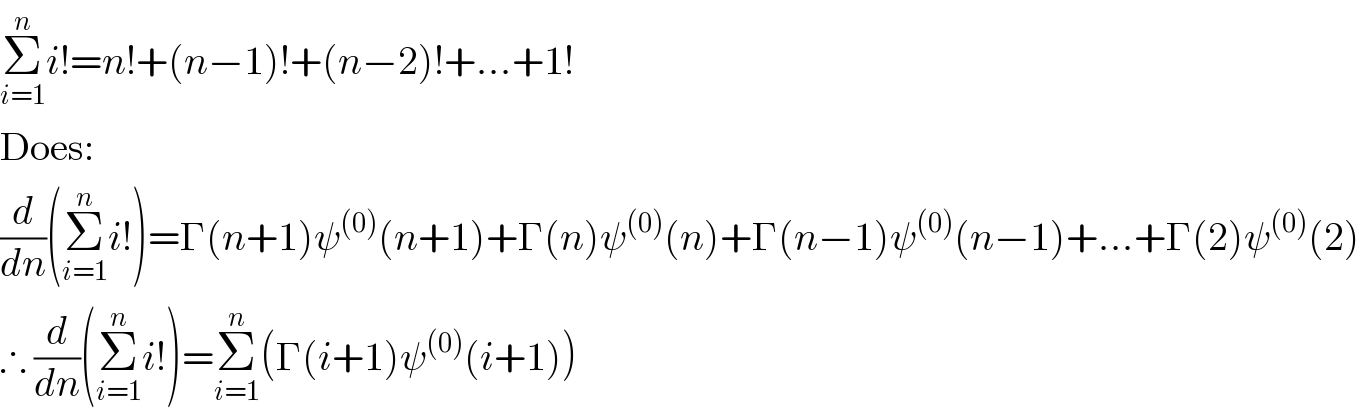
$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{i}!={n}!+\left({n}−\mathrm{1}\right)!+\left({n}−\mathrm{2}\right)!+…+\mathrm{1}! \\ $$$$\mathrm{Does}: \\ $$$$\frac{{d}}{{dn}}\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{i}!\right)=\Gamma\left({n}+\mathrm{1}\right)\psi^{\left(\mathrm{0}\right)} \left({n}+\mathrm{1}\right)+\Gamma\left({n}\right)\psi^{\left(\mathrm{0}\right)} \left({n}\right)+\Gamma\left({n}−\mathrm{1}\right)\psi^{\left(\mathrm{0}\right)} \left({n}−\mathrm{1}\right)+…+\Gamma\left(\mathrm{2}\right)\psi^{\left(\mathrm{0}\right)} \left(\mathrm{2}\right) \\ $$$$\therefore\:\frac{{d}}{{dn}}\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{i}!\right)=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\Gamma\left({i}+\mathrm{1}\right)\psi^{\left(\mathrm{0}\right)} \left({i}+\mathrm{1}\right)\right) \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com