Menu Close

lim-x-0-1-1-4x-cos-x-2-x-3-arctan-x-5-

Tinku Tara 0 Comments
Pin




Question Number 72462 by 20190927 last updated on 29/Oct/19
lim_(x→0) ((1−(√(1+4x ))cos(x^2 ))/(x^3 arctan(x^5 )))
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{4x}\:}\mathrm{cos}\left(\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{3}} \mathrm{arctan}\left(\mathrm{x}^{\mathrm{5}} \right)} \\ $$
Commented by kaivan.ahmadi last updated on 29/Oct/19
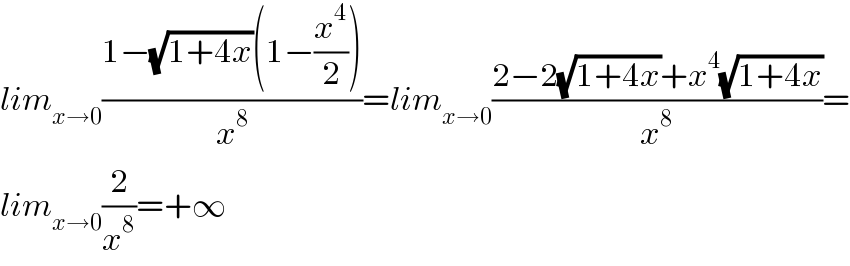
lim_(x→0) ((1−(√(1+4x))(1−(x^4 /2)))/x^8 )=lim_(x→0) ((2−2(√(1+4x))+x^4 (√(1+4x)))/x^8 )= lim_(x→0) (2/x^8 )=+∞
$${lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{4}{x}}\left(\mathrm{1}−\frac{{x}^{\mathrm{4}} }{\mathrm{2}}\right)}{{x}^{\mathrm{8}} }={lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{2}−\mathrm{2}\sqrt{\mathrm{1}+\mathrm{4}{x}}+{x}^{\mathrm{4}} \sqrt{\mathrm{1}+\mathrm{4}{x}}}{{x}^{\mathrm{8}} }= \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{2}}{{x}^{\mathrm{8}} }=+\infty \\ $$
Commented by mathmax by abdo last updated on 29/Oct/19
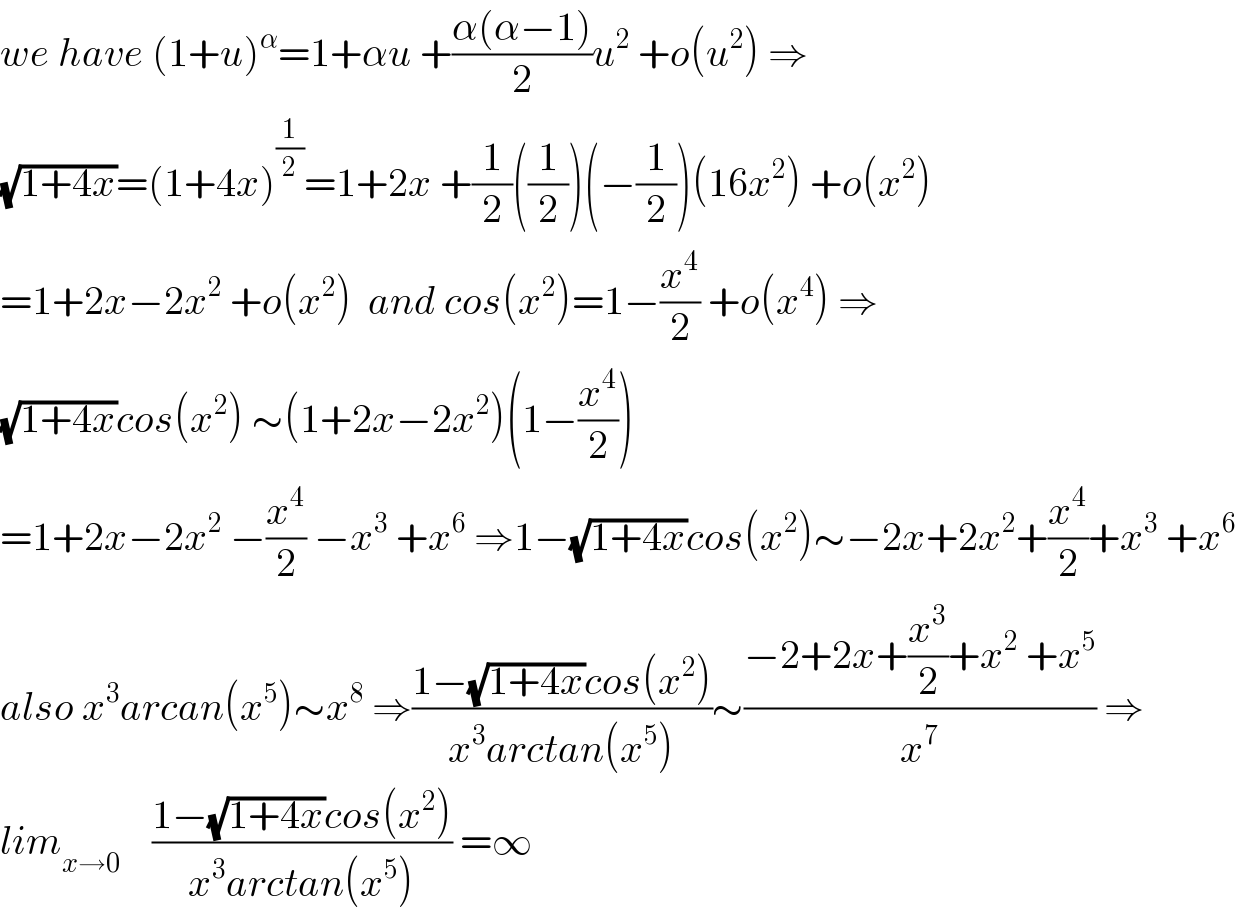
we have (1+u)^α =1+αu +((α(α−1))/2)u^2 +o(u^2 ) ⇒ (√(1+4x))=(1+4x)^(1/2) =1+2x +(1/2)((1/2))(−(1/2))(16x^2 ) +o(x^2 ) =1+2x−2x^2 +o(x^2 ) and cos(x^2 )=1−(x^4 /2) +o(x^4 ) ⇒ (√(1+4x))cos(x^2 ) ∼(1+2x−2x^2 )(1−(x^4 /2)) =1+2x−2x^2 −(x^4 /2) −x^3 +x^6 ⇒1−(√(1+4x))cos(x^2 )∼−2x+2x^2 +(x^4 /2)+x^3 +x^6 also x^3 arcan(x^5 )∼x^8 ⇒((1−(√(1+4x))cos(x^2 ))/(x^3 arctan(x^5 )))∼((−2+2x+(x^3 /2)+x^2 +x^5 )/x^7 ) ⇒ lim_(x→0) ((1−(√(1+4x))cos(x^2 ))/(x^3 arctan(x^5 ))) =∞
$${we}\:{have}\:\left(\mathrm{1}+{u}\right)^{\alpha} =\mathrm{1}+\alpha{u}\:+\frac{\alpha\left(\alpha−\mathrm{1}\right)}{\mathrm{2}}{u}^{\mathrm{2}} \:+{o}\left({u}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\sqrt{\mathrm{1}+\mathrm{4}{x}}=\left(\mathrm{1}+\mathrm{4}{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{1}+\mathrm{2}{x}\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{16}{x}^{\mathrm{2}} \right)\:+{o}\left({x}^{\mathrm{2}} \right) \\ $$$$=\mathrm{1}+\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} \:+{o}\left({x}^{\mathrm{2}} \right)\:\:{and}\:{cos}\left({x}^{\mathrm{2}} \right)=\mathrm{1}−\frac{{x}^{\mathrm{4}} }{\mathrm{2}}\:+{o}\left({x}^{\mathrm{4}} \right)\:\Rightarrow \\ $$$$\sqrt{\mathrm{1}+\mathrm{4}{x}}{cos}\left({x}^{\mathrm{2}} \right)\:\sim\left(\mathrm{1}+\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\frac{{x}^{\mathrm{4}} }{\mathrm{2}}\right) \\ $$$$=\mathrm{1}+\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} \:−\frac{{x}^{\mathrm{4}} }{\mathrm{2}}\:−{x}^{\mathrm{3}} \:+{x}^{\mathrm{6}} \:\Rightarrow\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{4}{x}}{cos}\left({x}^{\mathrm{2}} \right)\sim−\mathrm{2}{x}+\mathrm{2}{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{4}} }{\mathrm{2}}+{x}^{\mathrm{3}} \:+{x}^{\mathrm{6}} \\ $$$${also}\:{x}^{\mathrm{3}} {arcan}\left({x}^{\mathrm{5}} \right)\sim{x}^{\mathrm{8}} \:\Rightarrow\frac{\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{4}{x}}{cos}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{3}} {arctan}\left({x}^{\mathrm{5}} \right)}\sim\frac{−\mathrm{2}+\mathrm{2}{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{2}}+{x}^{\mathrm{2}} \:+{x}^{\mathrm{5}} }{{x}^{\mathrm{7}} }\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\frac{\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{4}{x}}{cos}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{3}} {arctan}\left({x}^{\mathrm{5}} \right)}\:=\infty \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *