Question Number 133091 by metamorfose last updated on 18/Feb/21
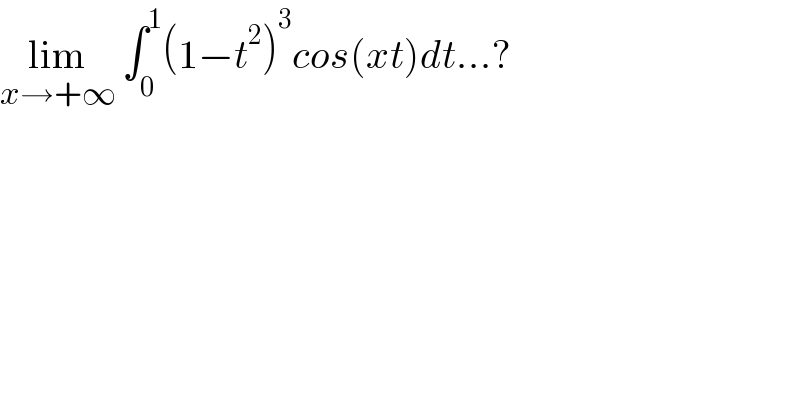
$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{3}} {cos}\left({xt}\right){dt}…? \\ $$
Answered by mnjuly1970 last updated on 18/Feb/21
![answer:=0 reiman −lebesgue theorem f is continuoues on[0,1] lim_(x→∞) ∫_0 ^( 1) f(t)sin(xt)dt=0](https://www.tinkutara.com/question/Q133096.png)
$${answer}:=\mathrm{0} \\ $$$${reiman}\:−{lebesgue}\:{theorem} \\ $$$$\:{f}\:\:{is}\:\:{continuoues}\:{on}\left[\mathrm{0},\mathrm{1}\right] \\ $$$$\:\:{lim}_{{x}\rightarrow\infty} \int_{\mathrm{0}} ^{\:\mathrm{1}} {f}\left({t}\right){sin}\left({xt}\right){dt}=\mathrm{0} \\ $$$$\:\:\: \\ $$
Answered by mathmax by abdo last updated on 20/Feb/21
![let f(t) is pritive of (1−t^2 )^3 by parts we get ∫_0 ^1 (1−t^2 )^3 cos(xt)dt =[((f(t))/x) sin(xt)]_0 ^1 −∫_0 ^1 ((f(t))/x)sin(xt)dt =((f(1)sin(x))/x) −(1/x)∫_0 ^1 f(t)sin(xt)dt ⇒ for x>0 ∣∫_0 ^1 (...)dt∣ ≤((∣f(1)∣)/x) +(1/x)∫_0 ^1 ∣f(t)∣ dt →0 (x→+∞) ⇒ lim_(x→+∞) ∫_0 ^1 (1−t^2 )^3 cos(xt)dt =0](https://www.tinkutara.com/question/Q133217.png)
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{t}\right)\:\mathrm{is}\:\mathrm{pritive}\:\mathrm{of}\:\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{3}} \:\mathrm{by}\:\mathrm{parts}\:\mathrm{we}\:\mathrm{get} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{3}} \:\mathrm{cos}\left(\mathrm{xt}\right)\mathrm{dt}\:=\left[\frac{\mathrm{f}\left(\mathrm{t}\right)}{\mathrm{x}}\:\mathrm{sin}\left(\mathrm{xt}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{f}\left(\mathrm{t}\right)}{\mathrm{x}}\mathrm{sin}\left(\mathrm{xt}\right)\mathrm{dt}\: \\ $$$$=\frac{\mathrm{f}\left(\mathrm{1}\right)\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{x}}\:−\frac{\mathrm{1}}{\mathrm{x}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{f}\left(\mathrm{t}\right)\mathrm{sin}\left(\mathrm{xt}\right)\mathrm{dt}\:\Rightarrow\:\mathrm{for}\:\mathrm{x}>\mathrm{0}\:\mid\int_{\mathrm{0}} ^{\mathrm{1}} \left(…\right)\mathrm{dt}\mid \\ $$$$\leqslant\frac{\mid\mathrm{f}\left(\mathrm{1}\right)\mid}{\mathrm{x}}\:+\frac{\mathrm{1}}{\mathrm{x}}\int_{\mathrm{0}} ^{\mathrm{1}} \mid\mathrm{f}\left(\mathrm{t}\right)\mid\:\mathrm{dt}\:\rightarrow\mathrm{0}\:\:\left(\mathrm{x}\rightarrow+\infty\right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{3}} \mathrm{cos}\left(\mathrm{xt}\right)\mathrm{dt}\:=\mathrm{0} \\ $$
