Question Number 139766 by mohammad17 last updated on 01/May/21
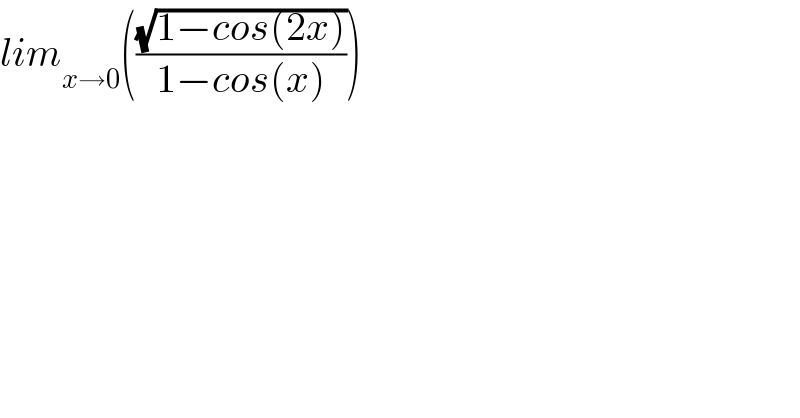
$${lim}_{{x}\rightarrow\mathrm{0}} \left(\frac{\sqrt{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}}{\mathrm{1}−{cos}\left({x}\right)}\right) \\ $$
Answered by bramlexs22 last updated on 01/May/21
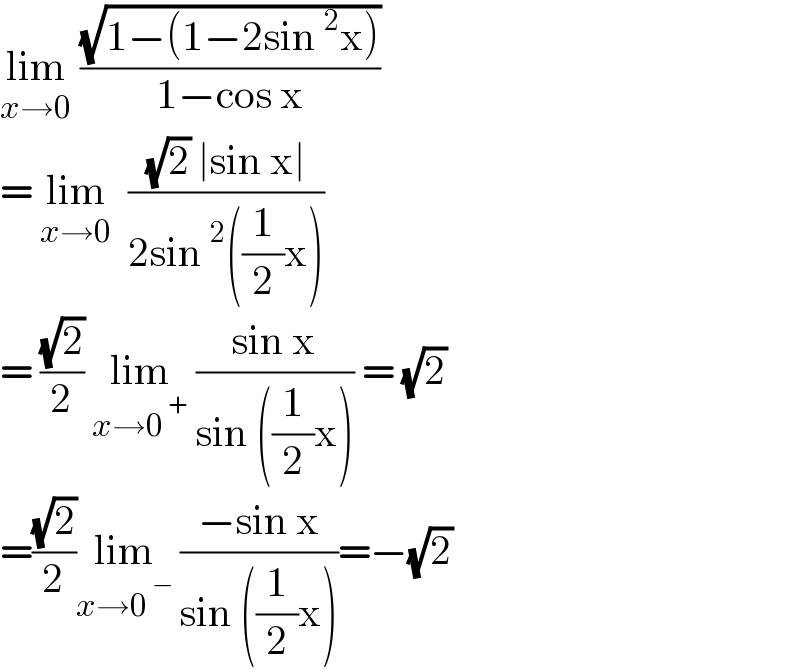
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}\right)}}{\mathrm{1}−\mathrm{cos}\:\mathrm{x}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\sqrt{\mathrm{2}}\:\mid\mathrm{sin}\:\mathrm{x}\mid}{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)} \\ $$$$=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\underset{{x}\rightarrow\mathrm{0}^{\:+} } {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)}\:=\:\sqrt{\mathrm{2}} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\underset{{x}\rightarrow\mathrm{0}^{\:−} } {\mathrm{lim}}\:\frac{−\mathrm{sin}\:\mathrm{x}}{\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)}=−\sqrt{\mathrm{2}}\: \\ $$
