Question Number 4964 by ankit chakravarti last updated on 27/Mar/16
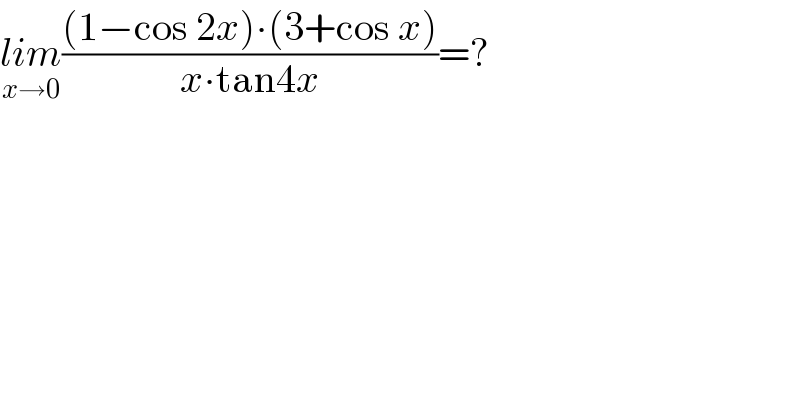
$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right)\centerdot\left(\mathrm{3}+\mathrm{cos}\:{x}\right)}{{x}\centerdot\mathrm{tan4}{x}}=? \\ $$$$ \\ $$
Answered by FilupSmith last updated on 29/Mar/16
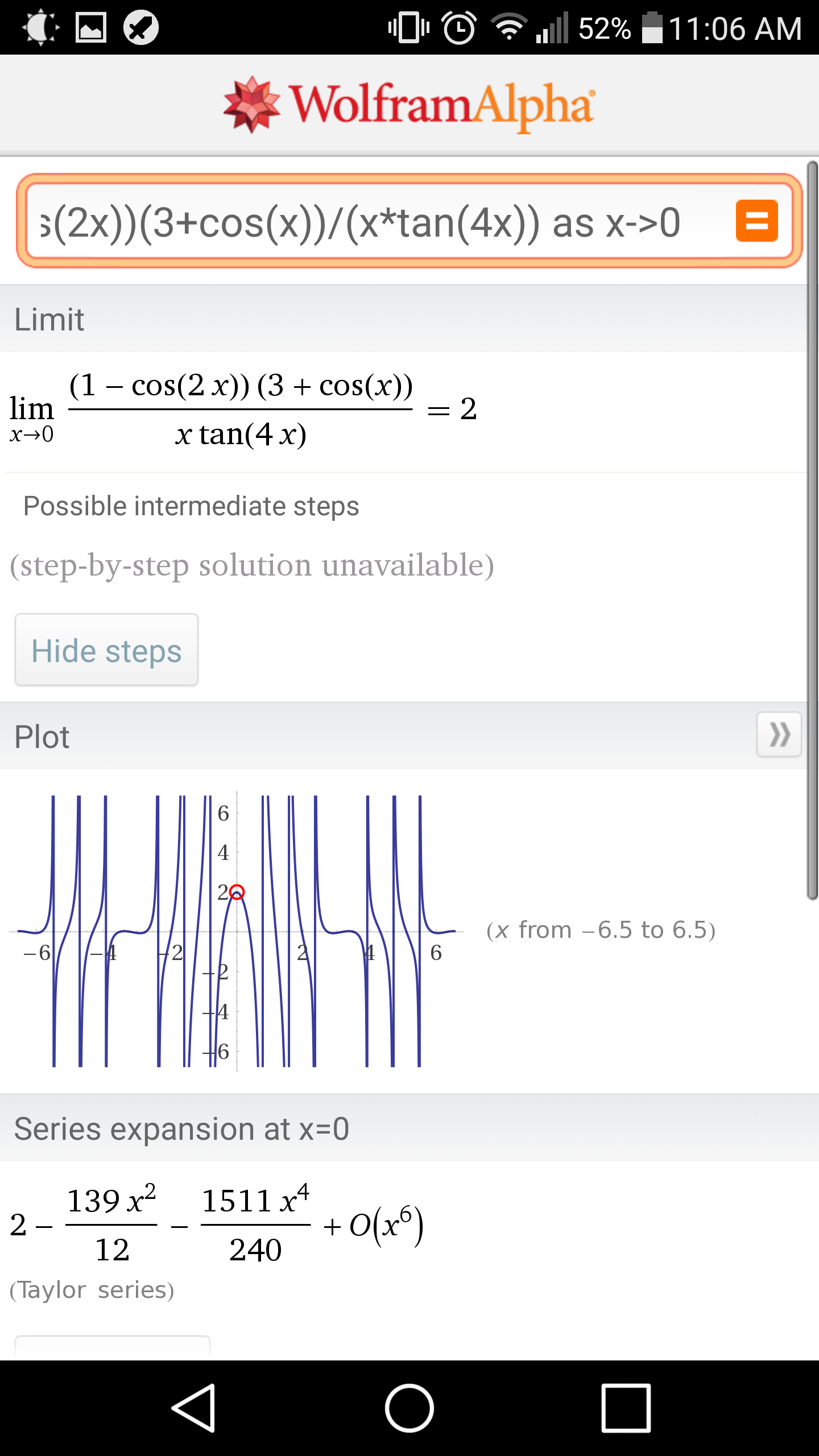
Commented by FilupSmith last updated on 29/Mar/16
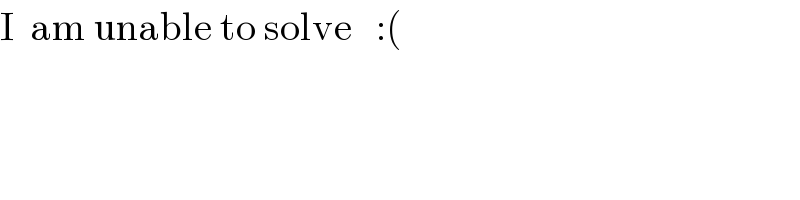
$$\mathrm{I}\:\:\mathrm{am}\:\mathrm{unable}\:\mathrm{to}\:\mathrm{solve}\:\:\::\left(\right. \\ $$
Commented by 123456 last updated on 29/Mar/16
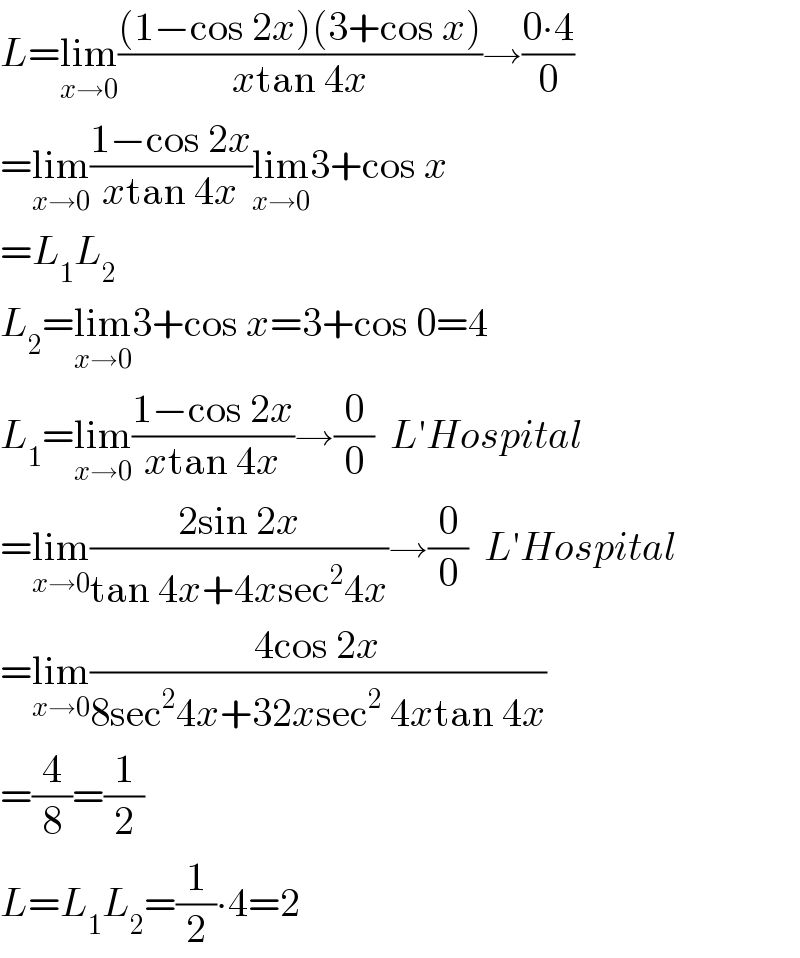
$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right)\left(\mathrm{3}+\mathrm{cos}\:{x}\right)}{{x}\mathrm{tan}\:\mathrm{4}{x}}\rightarrow\frac{\mathrm{0}\centerdot\mathrm{4}}{\mathrm{0}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}}{{x}\mathrm{tan}\:\mathrm{4}{x}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}3}+\mathrm{cos}\:{x} \\ $$$$={L}_{\mathrm{1}} {L}_{\mathrm{2}} \\ $$$${L}_{\mathrm{2}} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}3}+\mathrm{cos}\:{x}=\mathrm{3}+\mathrm{cos}\:\mathrm{0}=\mathrm{4} \\ $$$${L}_{\mathrm{1}} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}}{{x}\mathrm{tan}\:\mathrm{4}{x}}\rightarrow\frac{\mathrm{0}}{\mathrm{0}}\:\:{L}'{Hospital} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}\:\mathrm{2}{x}}{\mathrm{tan}\:\mathrm{4}{x}+\mathrm{4}{x}\mathrm{sec}^{\mathrm{2}} \mathrm{4}{x}}\rightarrow\frac{\mathrm{0}}{\mathrm{0}}\:\:{L}'{Hospital} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{4cos}\:\mathrm{2}{x}}{\mathrm{8sec}^{\mathrm{2}} \mathrm{4}{x}+\mathrm{32}{x}\mathrm{sec}^{\mathrm{2}} \:\mathrm{4}{x}\mathrm{tan}\:\mathrm{4}{x}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${L}={L}_{\mathrm{1}} {L}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\centerdot\mathrm{4}=\mathrm{2} \\ $$
Answered by Rojaye Shegz last updated on 30/Mar/16
![Multiply through by 1/4x^2 [lim (((1/4x^2 )(1−cos 2x).(3+cos x))/((1/4x^2 )x.tan4x))]_(x→0) ⇒(1/4)[lim((((((1−cos 2x))/x^2 ))(3+cos x))/((tan4x)/(4x)))]_(x→0) ⇒(1/4)[lim(((((2sin^2 x)/x^2 ))(3+cos x))/1)]_(x→0) (1−cos 2x=2sin^2 x, [lim(((tan x)/x))]_(x→0) =1) ⇒(1/4)[lim 2×1(3+cos x)]_(x→0) ([lim ((sin x)/x)]_(x→0) =1) ⇒(1/4)[lim 2(3+1)]_(x→0) (cos0=1) ⇒(1/4)×2×4 ⇒2](https://www.tinkutara.com/question/Q4999.png)
$${Multiply}\:{through}\:{by}\:\mathrm{1}/\mathrm{4}{x}^{\mathrm{2}} \\ $$$$\left[{lim}\:\frac{\left(\mathrm{1}/\mathrm{4}{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right).\left(\mathrm{3}+\mathrm{cos}\:{x}\right)}{\left(\mathrm{1}/\mathrm{4}{x}^{\mathrm{2}} \right){x}.\mathrm{tan4}{x}}\right]_{{x}\rightarrow\mathrm{0}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}\left[{lim}\frac{\left(\frac{\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right)}{{x}^{\mathrm{2}} }\right)\left(\mathrm{3}+\mathrm{cos}\:{x}\right)}{\frac{\mathrm{tan4}{x}}{\mathrm{4}{x}}}\right]_{{x}\rightarrow\mathrm{0}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}\left[{lim}\frac{\left(\frac{\mathrm{2sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }\right)\left(\mathrm{3}+\mathrm{cos}\:{x}\right)}{\mathrm{1}}\right]_{{x}\rightarrow\mathrm{0}} \:\:\:\:\:\:\:\:\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}=\mathrm{2sin}^{\mathrm{2}} {x},\:\left[{lim}\left(\frac{\mathrm{tan}\:{x}}{{x}}\right)\right]_{{x}\rightarrow\mathrm{0}} =\mathrm{1}\right) \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}\left[{lim}\:\mathrm{2}×\mathrm{1}\left(\mathrm{3}+\mathrm{cos}\:{x}\right)\right]_{{x}\rightarrow\mathrm{0}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\left[{lim}\:\frac{\mathrm{sin}\:{x}}{{x}}\right]_{{x}\rightarrow\mathrm{0}} =\mathrm{1}\right) \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}\left[{lim}\:\mathrm{2}\left(\mathrm{3}+\mathrm{1}\right)\right]_{{x}\rightarrow\mathrm{0}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{cos0}=\mathrm{1}\right) \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{2}×\mathrm{4} \\ $$$$\Rightarrow\mathrm{2} \\ $$
