Menu Close

lim-x-0-1-e-sin-x-ln-cos-x-x-3-

Tinku Tara 0 Comments
Pin




Question Number 142277 by liberty last updated on 29/May/21
lim_(x→0) ((1−e^(sin x ln (cos x)) )/x^3 ) =?
$$\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−{e}^{\mathrm{sin}\:{x}\:\mathrm{ln}\:\left(\mathrm{cos}\:{x}\right)} }{{x}^{\mathrm{3}} }\:=? \\ $$
Answered by Dwaipayan Shikari last updated on 29/May/21
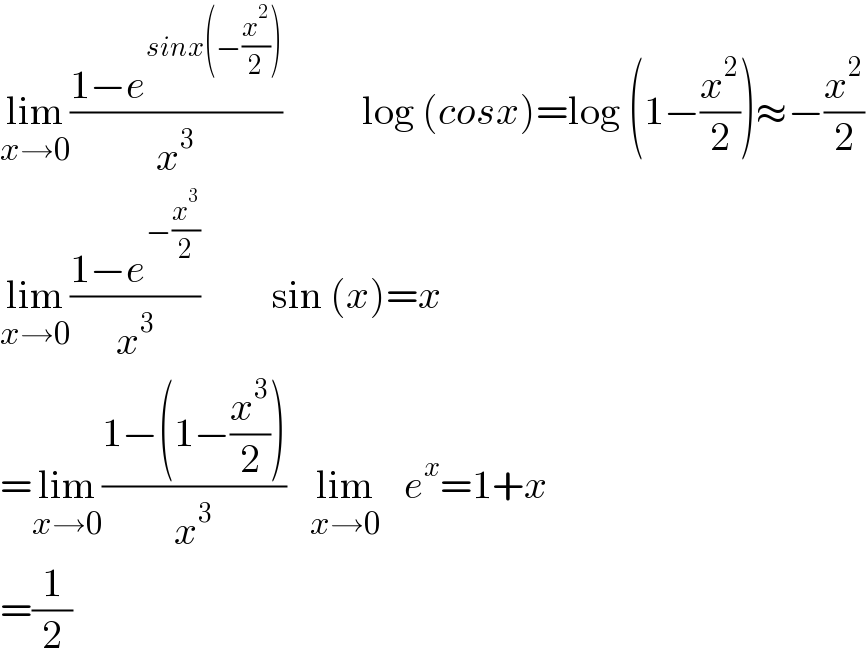
lim_(x→0) ((1−e^(sinx(−(x^2 /2))) )/x^3 ) log (cosx)=log (1−(x^2 /2))≈−(x^2 /2) lim_(x→0) ((1−e^(−(x^3 /2)) )/x^3 ) sin (x)=x =lim_(x→0) ((1−(1−(x^3 /2)))/x^3 ) lim_(x→0) e^x =1+x =(1/2)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−{e}^{{sinx}\left(−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)} }{{x}^{\mathrm{3}} }\:\:\:\:\:\:\:\:\:\:\mathrm{log}\:\left({cosx}\right)=\mathrm{log}\:\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\approx−\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−{e}^{−\frac{{x}^{\mathrm{3}} }{\mathrm{2}}} }{{x}^{\mathrm{3}} }\:\:\:\:\:\:\:\:\:\mathrm{sin}\:\left({x}\right)={x} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\left(\mathrm{1}−\frac{{x}^{\mathrm{3}} }{\mathrm{2}}\right)}{{x}^{\mathrm{3}} }\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:{e}^{{x}} =\mathrm{1}+{x} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by liberty last updated on 29/May/21
lim_(x→0) ((1−e^(sin x ln (1+cos x−1)) )/x^3 ) = lim_(x→1) ((1−e^(sin x(cos x−1)) )/x^3 ) = lim_(x→1) ((1−e^((x−(x^3 /6))(−(1/2)x^2 )) )/x^3 ) = lim_(x→1) ((1−(1−(1/2)x^3 (1−(x^2 /6))))/x^3 ) = lim_(x→1) (((1/2)x^3 (1−(x^2 /6)))/x^3 ) = (1/2)
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−{e}^{\mathrm{sin}\:{x}\:\mathrm{ln}\:\left(\mathrm{1}+\mathrm{cos}\:{x}−\mathrm{1}\right)} }{{x}^{\mathrm{3}} }\: \\ $$$$=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}−{e}^{\mathrm{sin}\:{x}\left(\mathrm{cos}\:{x}−\mathrm{1}\right)} }{{x}^{\mathrm{3}} } \\ $$$$=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}−{e}^{\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)\left(−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right)} }{{x}^{\mathrm{3}} } \\ $$$$=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{3}} \left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\right)\right)}{{x}^{\mathrm{3}} } \\ $$$$=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{3}} \left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\right)}{{x}^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 29/May/21
nice solution : thank you so much..
$${nice}\:{solution}\::\:{thank}\:{you}\:{so}\:{much}.. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *