Menu Close

lim-x-0-1-x-2-1-3-1-2x-1-4-x-x-2-lim-x-1-7-x-2-1-3-3-x-2-x-1-

Tinku Tara 0 Comments
Pin




Question Number 143064 by EDWIN88 last updated on 09/Jun/21
lim_(x→0) ((((1+x^2 ))^(1/3) −((1−2x))^(1/4) )/(x+x^2 )) =? lim_(x→1) ((((7+x^2 ))^(1/3) −(√(3+x^2 )))/(x−1)) =?
$$\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:−\sqrt[{\mathrm{4}}]{\mathrm{1}−\mathrm{2x}}}{\mathrm{x}+\mathrm{x}^{\mathrm{2}} }\:=? \\ $$$$\:\:\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{7}+\mathrm{x}^{\mathrm{2}} }−\sqrt{\mathrm{3}+\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}−\mathrm{1}}\:=? \\ $$
Answered by bramlexs22 last updated on 09/Jun/21
Answered by Mathspace last updated on 09/Jun/21
f(x)=(((1+x^2 )^3 −(1−2x)^(1/4) )/(x^(2 ) +x)) ⇒ f(x)∼((1+3x^2 −(1−(x/2)))/(x^2 +x)) ⇒ f(x)∼((3x^2 +(x/2))/(x^2 +x))=((3x+(1/2))/(x+1)) ⇒ lim_(x→0) f(x)=(1/2)
$${f}\left({x}\right)=\frac{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} −\left(\mathrm{1}−\mathrm{2}{x}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }{{x}^{\mathrm{2}\:} +{x}}\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\frac{\mathrm{1}+\mathrm{3}{x}^{\mathrm{2}} −\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)}{{x}^{\mathrm{2}} +{x}}\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\frac{\mathrm{3}{x}^{\mathrm{2}} \:+\frac{{x}}{\mathrm{2}}}{{x}^{\mathrm{2}} +{x}}=\frac{\mathrm{3}{x}+\frac{\mathrm{1}}{\mathrm{2}}}{{x}+\mathrm{1}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by Mathspace last updated on 09/Jun/21
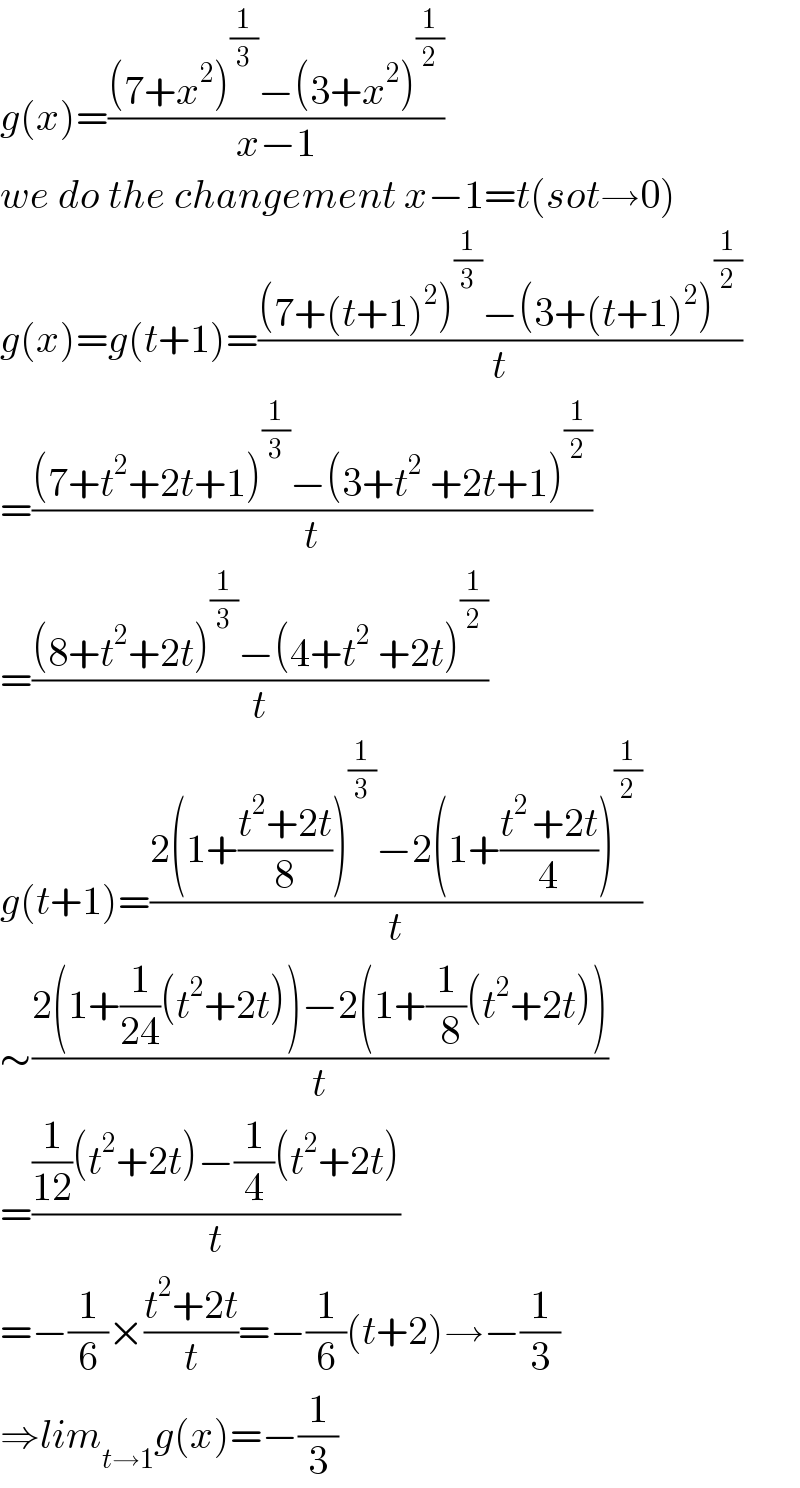
g(x)=(((7+x^2 )^(1/3) −(3+x^2 )^(1/2) )/(x−1)) we do the changement x−1=t(sot→0) g(x)=g(t+1)=(((7+(t+1)^2 )^(1/3) −(3+(t+1)^2 )^(1/2) )/t) =(((7+t^2 +2t+1)^(1/3) −(3+t^2 +2t+1)^(1/2) )/t) =(((8+t^2 +2t)^(1/3) −(4+t^2 +2t)^(1/2) )/t) g(t+1)=((2(1+((t^2 +2t)/8))^(1/3) −2(1+((t^(2 ) +2t)/4))^(1/2) )/t) ∼((2(1+(1/(24))(t^2 +2t))−2(1+(1/( 8))(t^2 +2t)))/t) =(((1/(12))(t^2 +2t)−(1/4)(t^2 +2t))/t) =−(1/6)×((t^2 +2t)/t)=−(1/6)(t+2)→−(1/3) ⇒lim_(t→1) g(x)=−(1/3)
$${g}\left({x}\right)=\frac{\left(\mathrm{7}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\left(\mathrm{3}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{{x}−\mathrm{1}} \\ $$$${we}\:{do}\:{the}\:{changement}\:{x}−\mathrm{1}={t}\left({sot}\rightarrow\mathrm{0}\right) \\ $$$${g}\left({x}\right)={g}\left({t}+\mathrm{1}\right)=\frac{\left(\mathrm{7}+\left({t}+\mathrm{1}\right)^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\left(\mathrm{3}+\left({t}+\mathrm{1}\right)^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{{t}} \\ $$$$=\frac{\left(\mathrm{7}+{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\left(\mathrm{3}+{t}^{\mathrm{2}} \:+\mathrm{2}{t}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{{t}} \\ $$$$=\frac{\left(\mathrm{8}+{t}^{\mathrm{2}} +\mathrm{2}{t}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\left(\mathrm{4}+{t}^{\mathrm{2}} \:+\mathrm{2}{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{{t}} \\ $$$${g}\left({t}+\mathrm{1}\right)=\frac{\mathrm{2}\left(\mathrm{1}+\frac{{t}^{\mathrm{2}} +\mathrm{2}{t}}{\mathrm{8}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{2}\left(\mathrm{1}+\frac{{t}^{\mathrm{2}\:} +\mathrm{2}{t}}{\mathrm{4}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{{t}} \\ $$$$\sim\frac{\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{24}}\left({t}^{\mathrm{2}} +\mathrm{2}{t}\right)\right)−\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{1}}{\:\mathrm{8}}\left({t}^{\mathrm{2}} +\mathrm{2}{t}\right)\right)}{{t}} \\ $$$$=\frac{\frac{\mathrm{1}}{\mathrm{12}}\left({t}^{\mathrm{2}} +\mathrm{2}{t}\right)−\frac{\mathrm{1}}{\mathrm{4}}\left({t}^{\mathrm{2}} +\mathrm{2}{t}\right)}{{t}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}×\frac{{t}^{\mathrm{2}} +\mathrm{2}{t}}{{t}}=−\frac{\mathrm{1}}{\mathrm{6}}\left({t}+\mathrm{2}\right)\rightarrow−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{lim}_{{t}\rightarrow\mathrm{1}} {g}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Answered by Olaf_Thorendsen last updated on 09/Jun/21
f(x) = ((((1+x^2 ))^(1/3) −((1−2x))^(1/4) )/(x+x^2 )) f(x) ∼_0 (((1+(1/3)x^2 )−(1+(1/4)(−2x)))/(x+x^2 )) f(x) ∼_0 (((1/3)x^2 +(1/2)x)/(x+x^2 )) → (1/2) g(x) = ((((7+x^2 ))^(1/3) −(√(3+x^2 )))/(x−1)) g(x+1) = ((((8+2x+x^2 ))^(1/3) −(√(4+2x+x^2 )))/x) g(x+1) = ((2((1+(1/4)x+(1/8)x^2 ))^(1/3) −2(√(1+(1/2)x+(1/4)x^2 )))/x) g(x+1) ∼_0 ((2(1+(1/3)((1/4)x+(1/8)x^2 ))−2(1+(1/2)((1/2)x+(1/4)x^2 )))/x) g(x+1) ∼_0 (((2/3)((1/4)x+(1/8)x^2 )−((1/2)x+(1/4)x^2 ))/x) → (1/6)−(1/2) = −(1/3)
$${f}\left({x}\right)\:=\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+{x}^{\mathrm{2}} }−\sqrt[{\mathrm{4}}]{\mathrm{1}−\mathrm{2}{x}}}{{x}+{x}^{\mathrm{2}} } \\ $$$${f}\left({x}\right)\:\underset{\mathrm{0}} {\sim}\:\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{2}} \right)−\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\left(−\mathrm{2}{x}\right)\right)}{{x}+{x}^{\mathrm{2}} } \\ $$$${f}\left({x}\right)\:\underset{\mathrm{0}} {\sim}\:\frac{\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{x}}{{x}+{x}^{\mathrm{2}} }\:\rightarrow\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${g}\left({x}\right)\:=\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{7}+{x}^{\mathrm{2}} }−\sqrt{\mathrm{3}+{x}^{\mathrm{2}} }}{{x}−\mathrm{1}} \\ $$$${g}\left({x}+\mathrm{1}\right)\:=\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{8}+\mathrm{2}{x}+{x}^{\mathrm{2}} }−\sqrt{\mathrm{4}+\mathrm{2}{x}+{x}^{\mathrm{2}} }}{{x}} \\ $$$${g}\left({x}+\mathrm{1}\right)\:=\:\frac{\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}{x}+\frac{\mathrm{1}}{\mathrm{8}}{x}^{\mathrm{2}} }−\mathrm{2}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{x}+\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{2}} }}{{x}} \\ $$$${g}\left({x}+\mathrm{1}\right)\:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{4}}{x}+\frac{\mathrm{1}}{\mathrm{8}}{x}^{\mathrm{2}} \right)\right)−\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}{x}+\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{2}} \right)\right)}{{x}} \\ $$$${g}\left({x}+\mathrm{1}\right)\:\underset{\mathrm{0}} {\sim}\:\frac{\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{4}}{x}+\frac{\mathrm{1}}{\mathrm{8}}{x}^{\mathrm{2}} \right)−\left(\frac{\mathrm{1}}{\mathrm{2}}{x}+\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{2}} \right)}{{x}}\:\rightarrow\:\frac{\mathrm{1}}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{2}}\:=\:−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *