Question Number 131181 by john_santu last updated on 02/Feb/21
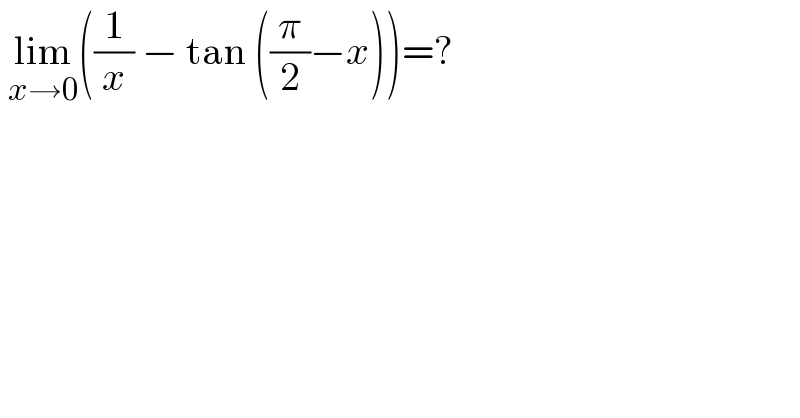
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}}\:−\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}−{x}\right)\right)=? \\ $$
Answered by Ar Brandon last updated on 02/Feb/21
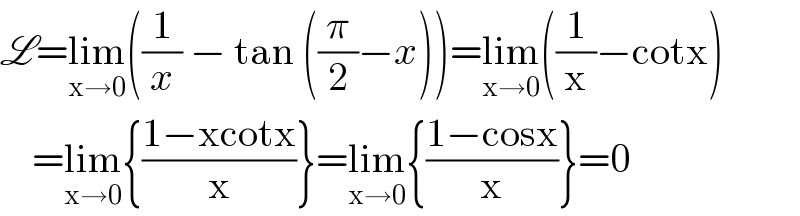
$$\mathscr{L}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}}\:−\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}−{x}\right)\right)=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{cotx}\right) \\ $$$$\:\:\:\:=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{\mathrm{1}−\mathrm{xcotx}}{\mathrm{x}}\right\}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{\mathrm{1}−\mathrm{cosx}}{\mathrm{x}}\right\}=\mathrm{0} \\ $$
Answered by john_santu last updated on 02/Feb/21

