Menu Close

lim-x-0-27-x-1-3-27-x-1-3-x-2-1-3-x-3-1-4-

Tinku Tara 0 Comments
Pin




Question Number 142351 by bramlexs22 last updated on 30/May/21
lim_(x→0) ((((27+x))^(1/(3 )) −((27−x))^(1/(3 )) )/( (x^2 )^(1/(3 )) + (x^3 )^(1/(4 )) )) =?
$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{27}+{x}}−\sqrt[{\mathrm{3}\:}]{\mathrm{27}−{x}}}{\:\sqrt[{\mathrm{3}\:}]{{x}^{\mathrm{2}} }\:+\:\sqrt[{\mathrm{4}\:}]{{x}^{\mathrm{3}} }}\:=? \\ $$
Answered by mathmax by abdo last updated on 30/May/21
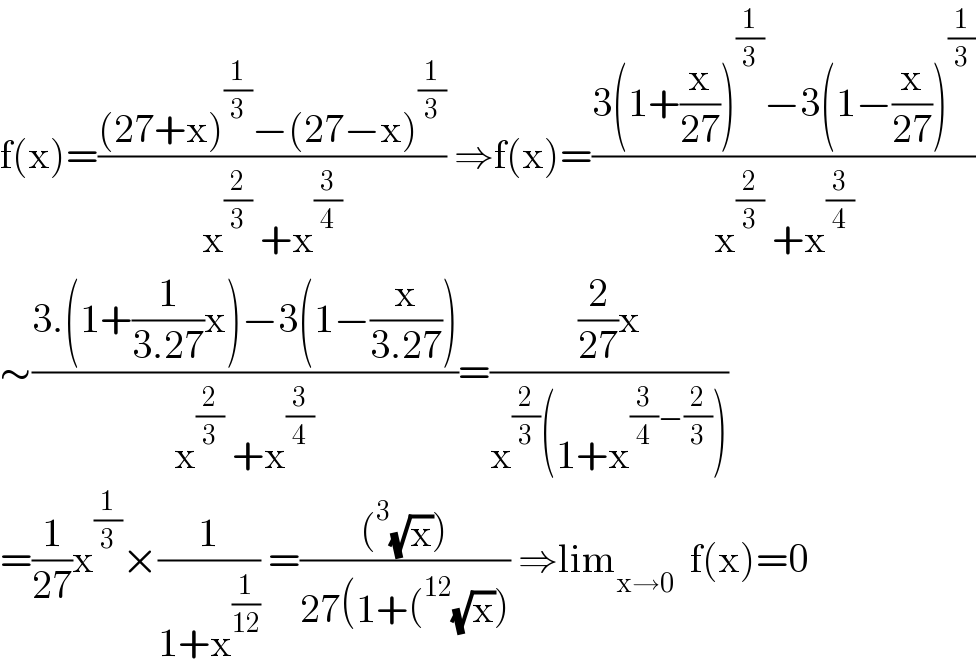
f(x)=(((27+x)^(1/3) −(27−x)^(1/3) )/(x^(2/3) +x^(3/4) )) ⇒f(x)=((3(1+(x/(27)))^(1/3) −3(1−(x/(27)))^(1/3) )/(x^(2/3) +x^(3/4) )) ∼((3.(1+(1/(3.27))x)−3(1−(x/(3.27))))/(x^(2/3) +x^(3/4) ))=(((2/(27))x)/(x^(2/3) (1+x^((3/4)−(2/3)) ))) =(1/(27))x^(1/3) ×(1/(1+x^(1/(12)) )) =(((^3 (√x)))/(27(1+(^(12) (√x)))) ⇒lim_(x→0) f(x)=0
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\left(\mathrm{27}+\mathrm{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\left(\mathrm{27}−\mathrm{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{\mathrm{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \:+\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{4}}} }\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{3}\left(\mathrm{1}+\frac{\mathrm{x}}{\mathrm{27}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{27}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{\mathrm{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \:+\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{4}}} } \\ $$$$\sim\frac{\mathrm{3}.\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}.\mathrm{27}}\mathrm{x}\right)−\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{3}.\mathrm{27}}\right)}{\mathrm{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \:+\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{4}}} }=\frac{\frac{\mathrm{2}}{\mathrm{27}}\mathrm{x}}{\mathrm{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \left(\mathrm{1}+\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{2}}{\mathrm{3}}} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{27}}\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{3}}} ×\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{12}}} }\:=\frac{\left(^{\mathrm{3}} \sqrt{\mathrm{x}}\right)}{\mathrm{27}\left(\mathrm{1}+\left(^{\mathrm{12}} \sqrt{\mathrm{x}}\right)\right.}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{0} \\ $$
Commented by mathmax by abdo last updated on 30/May/21
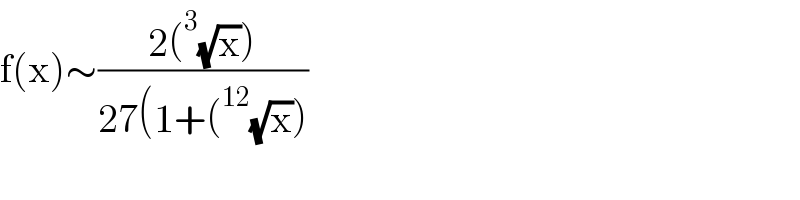
f(x)∼((2(^3 (√x)))/(27(1+(^(12) (√x))))
$$\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{2}\left(^{\mathrm{3}} \sqrt{\mathrm{x}}\right)}{\mathrm{27}\left(\mathrm{1}+\left(^{\mathrm{12}} \sqrt{\mathrm{x}}\right)\right.} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *