Question Number 71317 by aliesam last updated on 13/Oct/19
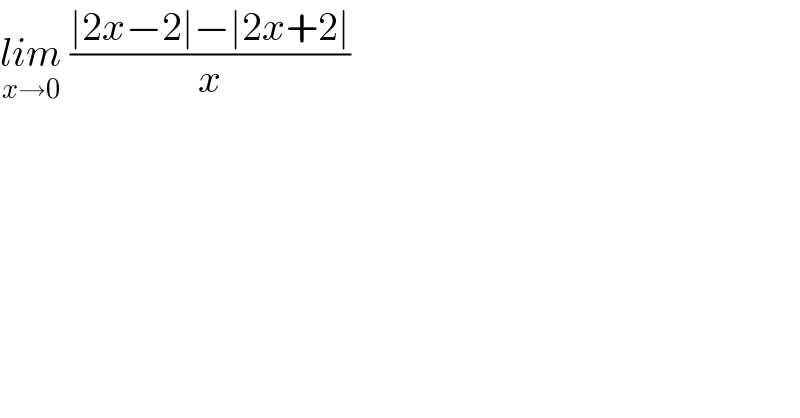
$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{\mid\mathrm{2}{x}−\mathrm{2}\mid−\mid\mathrm{2}{x}+\mathrm{2}\mid}{{x}} \\ $$
Commented by mathmax by abdo last updated on 13/Oct/19
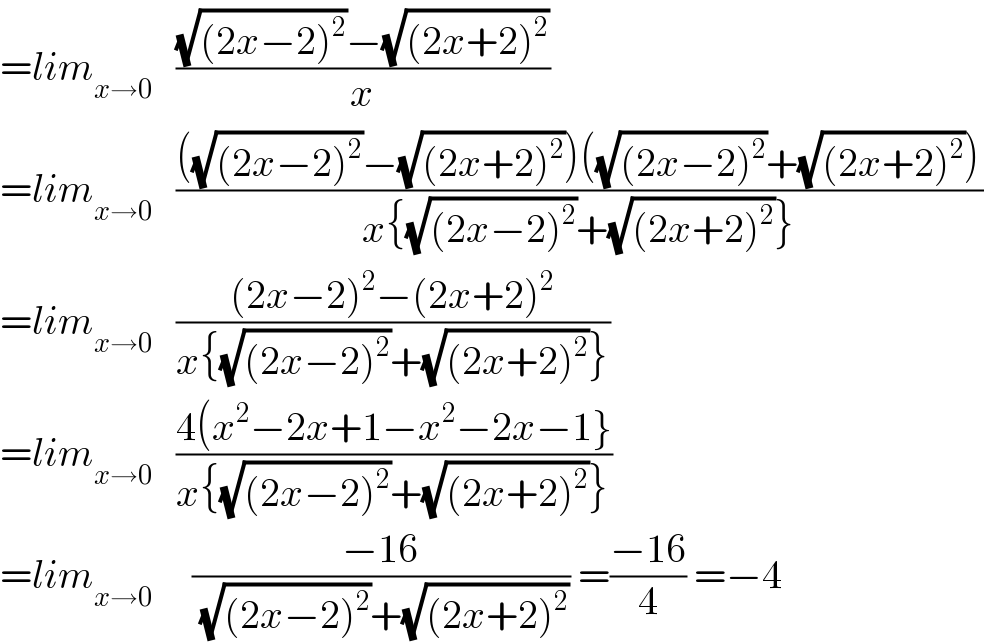
$$={lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{\sqrt{\left(\mathrm{2}{x}−\mathrm{2}\right)^{\mathrm{2}} }−\sqrt{\left(\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }}{{x}} \\ $$$$={lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{\left(\sqrt{\left(\mathrm{2}{x}−\mathrm{2}\right)^{\mathrm{2}} }−\sqrt{\left(\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }\right)\left(\sqrt{\left(\mathrm{2}{x}−\mathrm{2}\right)^{\mathrm{2}} }+\sqrt{\left(\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }\right)}{{x}\left\{\sqrt{\left(\mathrm{2}{x}−\mathrm{2}\right)^{\mathrm{2}} }+\sqrt{\left(\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }\right\}} \\ $$$$={lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{\left(\mathrm{2}{x}−\mathrm{2}\right)^{\mathrm{2}} −\left(\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }{{x}\left\{\sqrt{\left(\mathrm{2}{x}−\mathrm{2}\right)^{\mathrm{2}} }+\sqrt{\left(\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }\right\}} \\ $$$$={lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{4}\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}−{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}\right\}}{{x}\left\{\sqrt{\left(\mathrm{2}{x}−\mathrm{2}\right)^{\mathrm{2}} }+\sqrt{\left(\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }\right\}} \\ $$$$={lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\:\frac{−\mathrm{16}}{\:\sqrt{\left(\mathrm{2}{x}−\mathrm{2}\right)^{\mathrm{2}} }+\sqrt{\left(\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }}\:=\frac{−\mathrm{16}}{\mathrm{4}}\:=−\mathrm{4} \\ $$
Commented by aliesam last updated on 13/Oct/19

$${god}\:{bless}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 13/Oct/19

$${thank}\:{you}\:{sir}. \\ $$
Answered by ajfour last updated on 13/Oct/19
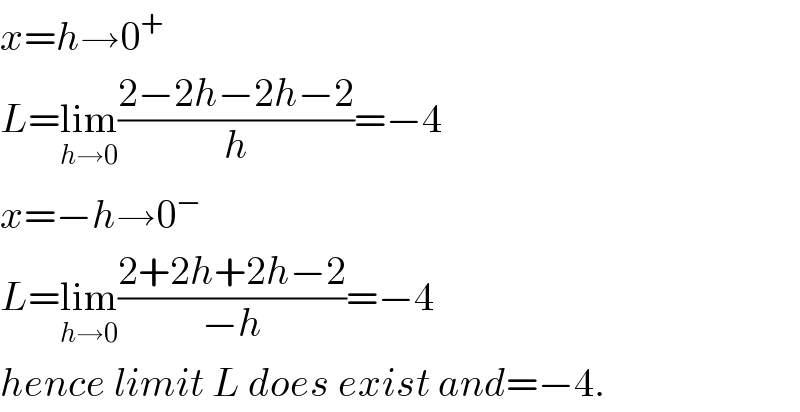
$${x}={h}\rightarrow\mathrm{0}^{+} \\ $$$${L}=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}−\mathrm{2}{h}−\mathrm{2}{h}−\mathrm{2}}{{h}}=−\mathrm{4} \\ $$$${x}=−{h}\rightarrow\mathrm{0}^{−} \\ $$$${L}=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}+\mathrm{2}{h}+\mathrm{2}{h}−\mathrm{2}}{−{h}}=−\mathrm{4} \\ $$$${hence}\:{limit}\:{L}\:{does}\:{exist}\:{and}=−\mathrm{4}. \\ $$
