Question Number 2265 by B744237509 last updated on 12/Nov/15
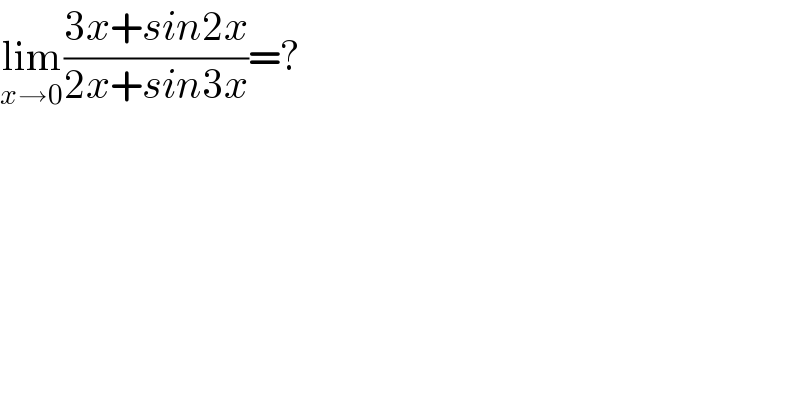
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}{x}+{sin}\mathrm{2}{x}}{\mathrm{2}{x}+{sin}\mathrm{3}{x}}=? \\ $$$$ \\ $$$$ \\ $$
Answered by Filup last updated on 12/Nov/15
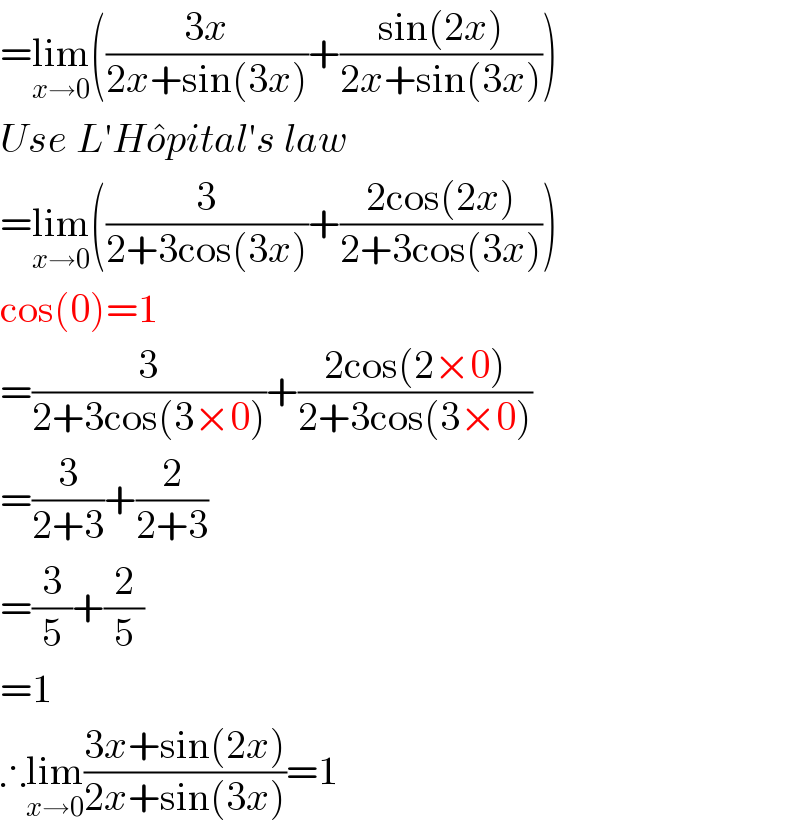
$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{3}{x}}{\mathrm{2}{x}+\mathrm{sin}\left(\mathrm{3}{x}\right)}+\frac{\mathrm{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}{x}+\mathrm{sin}\left(\mathrm{3}{x}\right)}\right) \\ $$$${Use}\:{L}'{H}\hat {{o}pital}'{s}\:{law} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{3}}{\mathrm{2}+\mathrm{3cos}\left(\mathrm{3}{x}\right)}+\frac{\mathrm{2cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}+\mathrm{3cos}\left(\mathrm{3}{x}\right)}\right) \\ $$$$\mathrm{cos}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}+\mathrm{3cos}\left(\mathrm{3}×\mathrm{0}\right)}+\frac{\mathrm{2cos}\left(\mathrm{2}×\mathrm{0}\right)}{\mathrm{2}+\mathrm{3cos}\left(\mathrm{3}×\mathrm{0}\right)} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}+\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{2}+\mathrm{3}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{5}}+\frac{\mathrm{2}}{\mathrm{5}} \\ $$$$=\mathrm{1} \\ $$$$\therefore\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}{x}+\mathrm{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}{x}+\mathrm{sin}\left(\mathrm{3}{x}\right)}=\mathrm{1} \\ $$
Commented by Filup last updated on 12/Nov/15

$$\mathrm{Expanding}\:\mathrm{the}\:\mathrm{fraction}\:\mathrm{into}\:\mathrm{two}\:\mathrm{parts} \\ $$$$\mathrm{isnt}\:\mathrm{nessisary}.\:\mathrm{You}\:\mathrm{can}\:\mathrm{start}\:\mathrm{on}\:\mathrm{line}\:\mathrm{2} \\ $$
Answered by Rasheed Soomro last updated on 12/Nov/15
![A way which doesn′t use derivative. lim_(x→0) ((3x+sin2x)/(2x+sin3x)) =lim_(x→0) ((((3x+sin2x)/(2x))×2x)/(((2x+sin3x)/(3x))×3x)) =(2/3)lim_(x→0) ((((3x)/(2x))+((sin 2x)/(2x)))/(((2x)/(3x))+((sin 3x)/(3x)))) =(2/3)lim_(x→0) (((3/2)+((sin 2x)/(2x)))/((2/3)+((sin 3x)/(3x)))) =(2/3)×(((3/2)+lim_(2x→0) ((sin 2x)/(2x)))/((2/3)+lim_(3x→0) ((sin 3x)/(3x)))) [x→0 { ((2x→0)),((3x→0)) :} ] =(2/3)×(((3/2)+1)/((2/3)+1)) [lim_(x→0) ((sin x)/x)=1] =(2/3)×(5/2)×(3/5)=1](https://www.tinkutara.com/question/Q2269.png)
$${A}\:{way}\:{which}\:{doesn}'{t}\:{use}\:{derivative}. \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}{x}+{sin}\mathrm{2}{x}}{\mathrm{2}{x}+{sin}\mathrm{3}{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{3}{x}+{sin}\mathrm{2}{x}}{\mathrm{2}{x}}×\mathrm{2}{x}}{\frac{\mathrm{2}{x}+{sin}\mathrm{3}{x}}{\mathrm{3}{x}}×\mathrm{3}{x}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\frac{\mathrm{3}{x}}{\mathrm{2}{x}}+\frac{{sin}\:\mathrm{2}{x}}{\mathrm{2}{x}}}{\frac{\mathrm{2}{x}}{\mathrm{3}{x}}+\frac{{sin}\:\mathrm{3}{x}}{\mathrm{3}{x}}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\frac{\mathrm{3}}{\mathrm{2}}+\frac{{sin}\:\mathrm{2}{x}}{\mathrm{2}{x}}}{\frac{\mathrm{2}}{\mathrm{3}}+\frac{{sin}\:\mathrm{3}{x}}{\mathrm{3}{x}}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\frac{\mathrm{3}}{\mathrm{2}}+\underset{\mathrm{2}{x}\rightarrow\mathrm{0}} {{lim}}\frac{{sin}\:\mathrm{2}{x}}{\mathrm{2}{x}}}{\frac{\mathrm{2}}{\mathrm{3}}+\underset{\mathrm{3}{x}\rightarrow\mathrm{0}} {{lim}}\frac{{sin}\:\mathrm{3}{x}}{\mathrm{3}{x}}}\:\:\:\:\:\left[{x}\rightarrow\mathrm{0\begin{cases}{\mathrm{2}{x}\rightarrow\mathrm{0}}\\{\mathrm{3}{x}\rightarrow\mathrm{0}}\end{cases}}\:\:\right] \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{1}}{\frac{\mathrm{2}}{\mathrm{3}}+\mathrm{1}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{sin}\:{x}}{{x}}=\mathrm{1}\right] \\ $$$$\:=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{5}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{5}}=\mathrm{1} \\ $$
Commented by Filup last updated on 12/Nov/15

$$\mathrm{I}\:\mathrm{knew}\:\mathrm{there}\:\mathrm{was}\:\mathrm{a}\:\mathrm{way}\:\mathrm{but}\:\mathrm{i}\:\mathrm{didnt}\:\mathrm{know} \\ $$$$\mathrm{how}\:\mathrm{to}\:\mathrm{do}\:\mathrm{it}.\:\mathrm{Nice}! \\ $$
Commented by B744237509 last updated on 12/Nov/15

$${thanx} \\ $$
