Menu Close

lim-x-0-4-sin-x-2-tan-x-6x-x-5-Without-L-Hospital-

Tinku Tara 0 Comments
Pin




Question Number 68521 by naka3546 last updated on 13/Sep/19
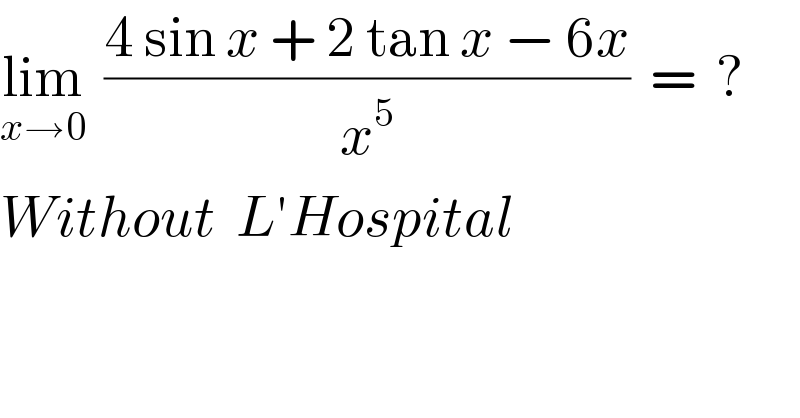
lim_(x→0) ((4 sin x + 2 tan x − 6x)/x^5 ) = ? Without L′Hospital
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{4}\:\mathrm{sin}\:{x}\:+\:\mathrm{2}\:\mathrm{tan}\:{x}\:−\:\mathrm{6}{x}}{{x}^{\mathrm{5}} }\:\:=\:\:? \\ $$$${Without}\:\:{L}'{Hospital} \\ $$
Commented by mathmax by abdo last updated on 13/Sep/19
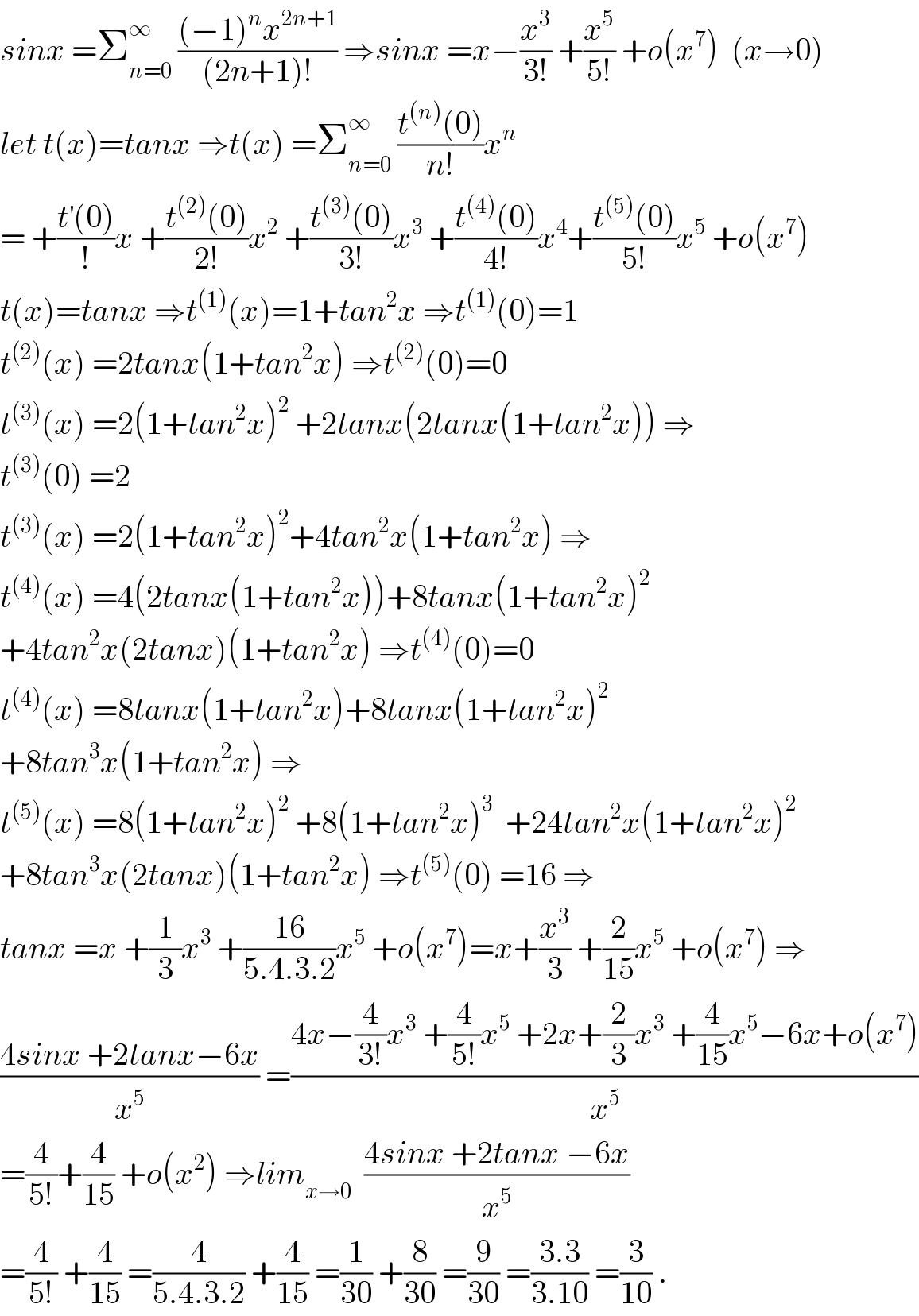
sinx =Σ_(n=0) ^∞ (((−1)^n x^(2n+1) )/((2n+1)!)) ⇒sinx =x−(x^3 /(3!)) +(x^5 /(5!)) +o(x^7 ) (x→0) let t(x)=tanx ⇒t(x) =Σ_(n=0) ^∞ ((t^((n)) (0))/(n!))x^n = +((t^′ (0))/!)x +((t^((2)) (0))/(2!))x^2 +((t^((3)) (0))/(3!))x^3 +((t^((4)) (0))/(4!))x^4 +((t^((5)) (0))/(5!))x^5 +o(x^7 ) t(x)=tanx ⇒t^((1)) (x)=1+tan^2 x ⇒t^((1)) (0)=1 t^((2)) (x) =2tanx(1+tan^2 x) ⇒t^((2)) (0)=0 t^((3)) (x) =2(1+tan^2 x)^2 +2tanx(2tanx(1+tan^2 x)) ⇒ t^((3)) (0) =2 t^((3)) (x) =2(1+tan^2 x)^2 +4tan^2 x(1+tan^2 x) ⇒ t^((4)) (x) =4(2tanx(1+tan^2 x))+8tanx(1+tan^2 x)^2 +4tan^2 x(2tanx)(1+tan^2 x) ⇒t^((4)) (0)=0 t^((4)) (x) =8tanx(1+tan^2 x)+8tanx(1+tan^2 x)^2 +8tan^3 x(1+tan^2 x) ⇒ t^((5)) (x) =8(1+tan^2 x)^2 +8(1+tan^2 x)^3 +24tan^2 x(1+tan^2 x)^2 +8tan^3 x(2tanx)(1+tan^2 x) ⇒t^((5)) (0) =16 ⇒ tanx =x +(1/3)x^3 +((16)/(5.4.3.2))x^5 +o(x^7 )=x+(x^3 /3) +(2/(15))x^5 +o(x^7 ) ⇒ ((4sinx +2tanx−6x)/x^5 ) =((4x−(4/(3!))x^3 +(4/(5!))x^5 +2x+(2/3)x^3 +(4/(15))x^5 −6x+o(x^7 ))/x^5 ) =(4/(5!))+(4/(15)) +o(x^2 ) ⇒lim_(x→0) ((4sinx +2tanx −6x)/x^5 ) =(4/(5!)) +(4/(15)) =(4/(5.4.3.2)) +(4/(15)) =(1/(30)) +(8/(30)) =(9/(30)) =((3.3)/(3.10)) =(3/(10)) .
$${sinx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:\Rightarrow{sinx}\:={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}\:+{o}\left({x}^{\mathrm{7}} \right)\:\:\left({x}\rightarrow\mathrm{0}\right) \\ $$$${let}\:{t}\left({x}\right)={tanx}\:\Rightarrow{t}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{t}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}{x}^{{n}} \\ $$$$=\:+\frac{{t}^{'} \left(\mathrm{0}\right)}{!}{x}\:+\frac{{t}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} \:+\frac{{t}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)}{\mathrm{3}!}{x}^{\mathrm{3}} \:+\frac{{t}^{\left(\mathrm{4}\right)} \left(\mathrm{0}\right)}{\mathrm{4}!}{x}^{\mathrm{4}} +\frac{{t}^{\left(\mathrm{5}\right)} \left(\mathrm{0}\right)}{\mathrm{5}!}{x}^{\mathrm{5}} \:+{o}\left({x}^{\mathrm{7}} \right) \\ $$$${t}\left({x}\right)={tanx}\:\Rightarrow{t}^{\left(\mathrm{1}\right)} \left({x}\right)=\mathrm{1}+{tan}^{\mathrm{2}} {x}\:\Rightarrow{t}^{\left(\mathrm{1}\right)} \left(\mathrm{0}\right)=\mathrm{1} \\ $$$${t}^{\left(\mathrm{2}\right)} \left({x}\right)\:=\mathrm{2}{tanx}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\:\Rightarrow{t}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)=\mathrm{0} \\ $$$${t}^{\left(\mathrm{3}\right)} \left({x}\right)\:=\mathrm{2}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)^{\mathrm{2}} \:+\mathrm{2}{tanx}\left(\mathrm{2}{tanx}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\right)\:\Rightarrow \\ $$$${t}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)\:=\mathrm{2} \\ $$$${t}^{\left(\mathrm{3}\right)} \left({x}\right)\:=\mathrm{2}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)^{\mathrm{2}} +\mathrm{4}{tan}^{\mathrm{2}} {x}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\:\Rightarrow \\ $$$${t}^{\left(\mathrm{4}\right)} \left({x}\right)\:=\mathrm{4}\left(\mathrm{2}{tanx}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\right)+\mathrm{8}{tanx}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)^{\mathrm{2}} \\ $$$$+\mathrm{4}{tan}^{\mathrm{2}} {x}\left(\mathrm{2}{tanx}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\:\Rightarrow{t}^{\left(\mathrm{4}\right)} \left(\mathrm{0}\right)=\mathrm{0} \\ $$$${t}^{\left(\mathrm{4}\right)} \left({x}\right)\:=\mathrm{8}{tanx}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)+\mathrm{8}{tanx}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)^{\mathrm{2}} \\ $$$$+\mathrm{8}{tan}^{\mathrm{3}} {x}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\:\Rightarrow \\ $$$${t}^{\left(\mathrm{5}\right)} \left({x}\right)\:=\mathrm{8}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)^{\mathrm{2}} \:+\mathrm{8}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)^{\mathrm{3}} \:\:+\mathrm{24}{tan}^{\mathrm{2}} {x}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)^{\mathrm{2}} \\ $$$$+\mathrm{8}{tan}^{\mathrm{3}} {x}\left(\mathrm{2}{tanx}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\:\Rightarrow{t}^{\left(\mathrm{5}\right)} \left(\mathrm{0}\right)\:=\mathrm{16}\:\Rightarrow \\ $$$${tanx}\:={x}\:+\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} \:+\frac{\mathrm{16}}{\mathrm{5}.\mathrm{4}.\mathrm{3}.\mathrm{2}}{x}^{\mathrm{5}} \:+{o}\left({x}^{\mathrm{7}} \right)={x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:+\frac{\mathrm{2}}{\mathrm{15}}{x}^{\mathrm{5}} \:+{o}\left({x}^{\mathrm{7}} \right)\:\Rightarrow \\ $$$$\frac{\mathrm{4}{sinx}\:+\mathrm{2}{tanx}−\mathrm{6}{x}}{{x}^{\mathrm{5}} }\:=\frac{\mathrm{4}{x}−\frac{\mathrm{4}}{\mathrm{3}!}{x}^{\mathrm{3}} \:+\frac{\mathrm{4}}{\mathrm{5}!}{x}^{\mathrm{5}} \:+\mathrm{2}{x}+\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{3}} \:+\frac{\mathrm{4}}{\mathrm{15}}{x}^{\mathrm{5}} −\mathrm{6}{x}+{o}\left({x}^{\mathrm{7}} \right)}{{x}^{\mathrm{5}} } \\ $$$$=\frac{\mathrm{4}}{\mathrm{5}!}+\frac{\mathrm{4}}{\mathrm{15}}\:+{o}\left({x}^{\mathrm{2}} \right)\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{4}{sinx}\:+\mathrm{2}{tanx}\:−\mathrm{6}{x}}{{x}^{\mathrm{5}} } \\ $$$$=\frac{\mathrm{4}}{\mathrm{5}!}\:+\frac{\mathrm{4}}{\mathrm{15}}\:=\frac{\mathrm{4}}{\mathrm{5}.\mathrm{4}.\mathrm{3}.\mathrm{2}}\:+\frac{\mathrm{4}}{\mathrm{15}}\:=\frac{\mathrm{1}}{\mathrm{30}}\:+\frac{\mathrm{8}}{\mathrm{30}}\:=\frac{\mathrm{9}}{\mathrm{30}}\:=\frac{\mathrm{3}.\mathrm{3}}{\mathrm{3}.\mathrm{10}}\:=\frac{\mathrm{3}}{\mathrm{10}}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *