Question Number 137773 by Ajadiazeemolamilekan last updated on 06/Apr/21
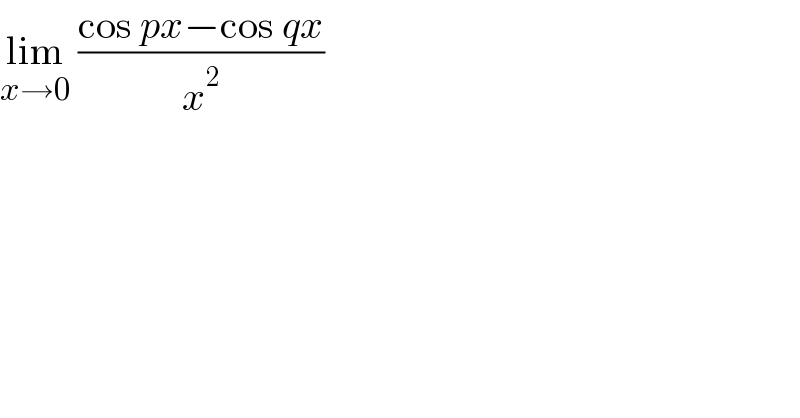
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:{px}−\mathrm{cos}\:{qx}}{{x}^{\mathrm{2}} } \\ $$
Answered by bemath last updated on 06/Apr/21
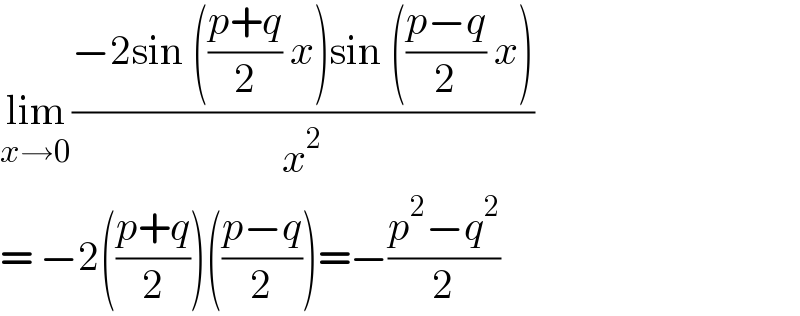
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2sin}\:\left(\frac{{p}+{q}}{\mathrm{2}}\:{x}\right)\mathrm{sin}\:\left(\frac{{p}−{q}}{\mathrm{2}}\:{x}\right)}{{x}^{\mathrm{2}} } \\ $$$$=\:−\mathrm{2}\left(\frac{{p}+{q}}{\mathrm{2}}\right)\left(\frac{{p}−{q}}{\mathrm{2}}\right)=−\frac{{p}^{\mathrm{2}} −{q}^{\mathrm{2}} }{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 07/Apr/21
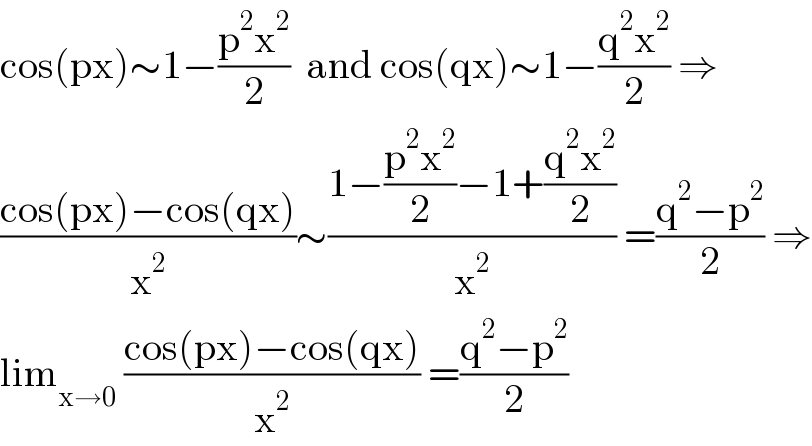
$$\mathrm{cos}\left(\mathrm{px}\right)\sim\mathrm{1}−\frac{\mathrm{p}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\:\mathrm{and}\:\mathrm{cos}\left(\mathrm{qx}\right)\sim\mathrm{1}−\frac{\mathrm{q}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\frac{\mathrm{cos}\left(\mathrm{px}\right)−\mathrm{cos}\left(\mathrm{qx}\right)}{\mathrm{x}^{\mathrm{2}} }\sim\frac{\mathrm{1}−\frac{\mathrm{p}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}+\frac{\mathrm{q}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }{\mathrm{2}}}{\mathrm{x}^{\mathrm{2}} }\:=\frac{\mathrm{q}^{\mathrm{2}} −\mathrm{p}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\frac{\mathrm{cos}\left(\mathrm{px}\right)−\mathrm{cos}\left(\mathrm{qx}\right)}{\mathrm{x}^{\mathrm{2}} }\:=\frac{\mathrm{q}^{\mathrm{2}} −\mathrm{p}^{\mathrm{2}} }{\mathrm{2}} \\ $$
