Menu Close

lim-x-0-f-a-x-b-a-x-f-a-x-b-Then-lim-x-f-x-

Tinku Tara
Pin




Question Number 368 by novrya last updated on 25/Jan/15
lim_(x→0) [f((a/x)+b)−(a/x)f ′((a/x)+b)]=α. Then lim_(x→∞) f(x)=....
$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\left[{f}\left(\frac{{a}}{{x}}+{b}\right)−\frac{{a}}{{x}}{f}\:'\left(\frac{{a}}{{x}}+{b}\right)\right]=\alpha.\:{Then} \\ $$$$\:{li}\underset{{x}\rightarrow\infty} {{m}f}\left({x}\right)=…. \\ $$$$ \\ $$$$ \\ $$
Commented by 123456 last updated on 24/Dec/14
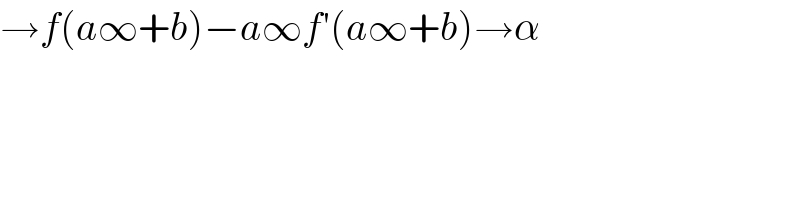
→f(a∞+b)−a∞f′(a∞+b)→α
$$\rightarrow{f}\left({a}\infty+{b}\right)−{a}\infty{f}'\left({a}\infty+{b}\right)\rightarrow\alpha \\ $$
Answered by prakash jain last updated on 25/Dec/14
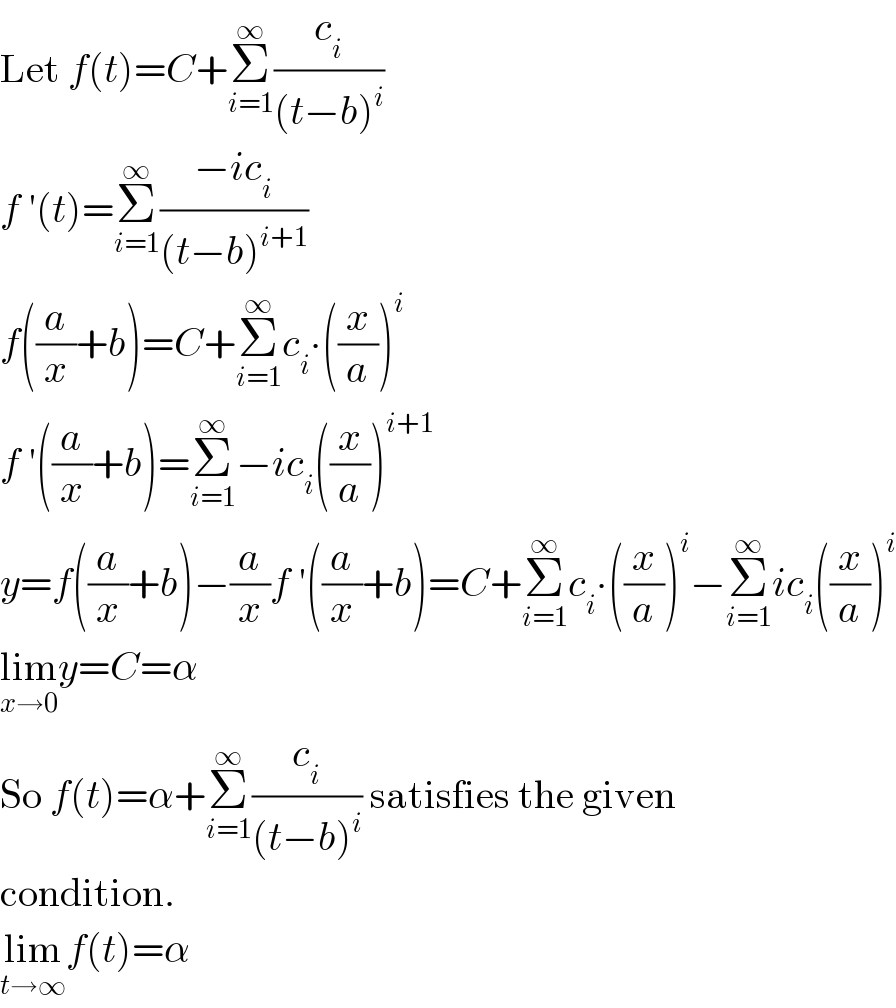
Let f(t)=C+Σ_(i=1) ^∞ (c_i /((t−b)^i )) f ′(t)=Σ_(i=1) ^∞ ((−ic_i )/((t−b)^(i+1) )) f((a/x)+b)=C+Σ_(i=1) ^∞ c_i ∙((x/a))^i f ′((a/x)+b)=Σ_(i=1) ^∞ −ic_i ((x/a))^(i+1) y=f((a/x)+b)−(a/x)f ′((a/x)+b)=C+Σ_(i=1) ^∞ c_i ∙((x/a))^i −Σ_(i=1) ^∞ ic_i ((x/a))^i lim_(x→0) y=C=α So f(t)=α+Σ_(i=1) ^∞ (c_i /((t−b)^i )) satisfies the given condition. lim_(t→∞) f(t)=α
$$\mathrm{Let}\:{f}\left({t}\right)={C}+\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{c}_{{i}} }{\left({t}−{b}\right)^{{i}} } \\ $$$${f}\:'\left({t}\right)=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{−{ic}_{{i}} }{\left({t}−{b}\right)^{{i}+\mathrm{1}} } \\ $$$${f}\left(\frac{{a}}{{x}}+{b}\right)={C}+\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{c}_{{i}} \centerdot\left(\frac{{x}}{{a}}\right)^{{i}} \\ $$$${f}\:'\left(\frac{{a}}{{x}}+{b}\right)=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}−{ic}_{{i}} \left(\frac{{x}}{{a}}\right)^{{i}+\mathrm{1}} \\ $$$${y}={f}\left(\frac{{a}}{{x}}+{b}\right)−\frac{{a}}{{x}}{f}\:'\left(\frac{{a}}{{x}}+{b}\right)={C}+\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{c}_{{i}} \centerdot\left(\frac{{x}}{{a}}\right)^{{i}} −\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{ic}_{{i}} \left(\frac{{x}}{{a}}\right)^{{i}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{y}={C}=\alpha \\ $$$$\mathrm{So}\:{f}\left({t}\right)=\alpha+\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{c}_{{i}} }{\left({t}−{b}\right)^{{i}} }\:\mathrm{satisfies}\:\mathrm{the}\:\mathrm{given} \\ $$$$\mathrm{condition}. \\ $$$$\underset{{t}\rightarrow\infty} {\mathrm{lim}}{f}\left({t}\right)=\alpha \\ $$

Pin