Question Number 12382 by tawa last updated on 21/Apr/17
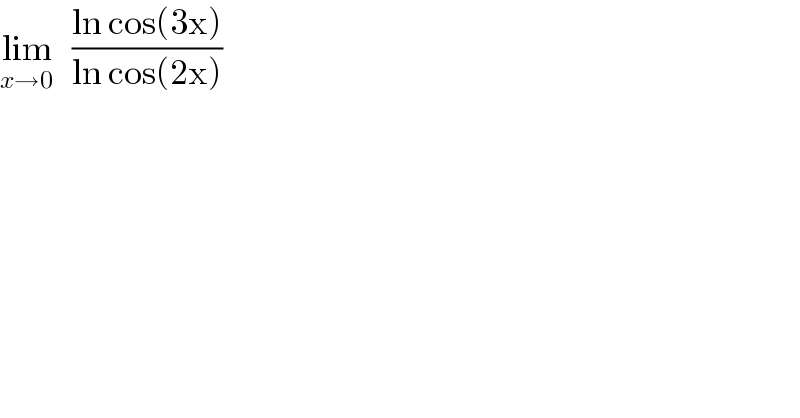
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{\mathrm{ln}\:\mathrm{cos}\left(\mathrm{3x}\right)}{\mathrm{ln}\:\mathrm{cos}\left(\mathrm{2x}\right)} \\ $$
Answered by ajfour last updated on 21/Apr/17
![=lim_(x→0) ((ln [1−(1−cos 3x)])/(ln [1−(1−cos 2x)])) =lim_(x→0) ((ln [1−2sin^2 (3x/2)])/(ln [1−2sin^2 x])) = lim_(x→0) ((−2sin^2 (3x/2))/(−2sin^2 x)) =lim_(x→0) (((3x/2)^2 )/x^2 ) = (9/4) .](https://www.tinkutara.com/question/Q12384.png)
$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left[\mathrm{1}−\left(\mathrm{1}−\mathrm{cos}\:\mathrm{3}{x}\right)\right]}{\mathrm{ln}\:\left[\mathrm{1}−\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right)\right]} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left[\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \left(\mathrm{3}{x}/\mathrm{2}\right)\right]}{\mathrm{ln}\:\left[\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}\right]} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2sin}\:^{\mathrm{2}} \left(\mathrm{3}{x}/\mathrm{2}\right)}{−\mathrm{2sin}\:^{\mathrm{2}} {x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{3}{x}/\mathrm{2}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{9}}{\mathrm{4}}\:. \\ $$
Commented by tawa last updated on 21/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$ \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 21/Apr/17
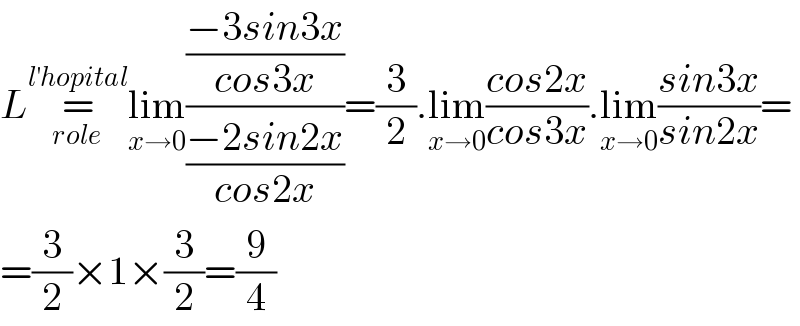
$${L}\underset{{role}} {\overset{{l}^{'} {hopital}} {=}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{−\mathrm{3}{sin}\mathrm{3}{x}}{{cos}\mathrm{3}{x}}}{\frac{−\mathrm{2}{sin}\mathrm{2}{x}}{{cos}\mathrm{2}{x}}}=\frac{\mathrm{3}}{\mathrm{2}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{cos}\mathrm{2}{x}}{{cos}\mathrm{3}{x}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{sin}\mathrm{3}{x}}{{sin}\mathrm{2}{x}}= \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}×\mathrm{1}×\frac{\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$
Commented by tawa last updated on 21/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
