Question Number 10137 by malwaan last updated on 26/Jan/17
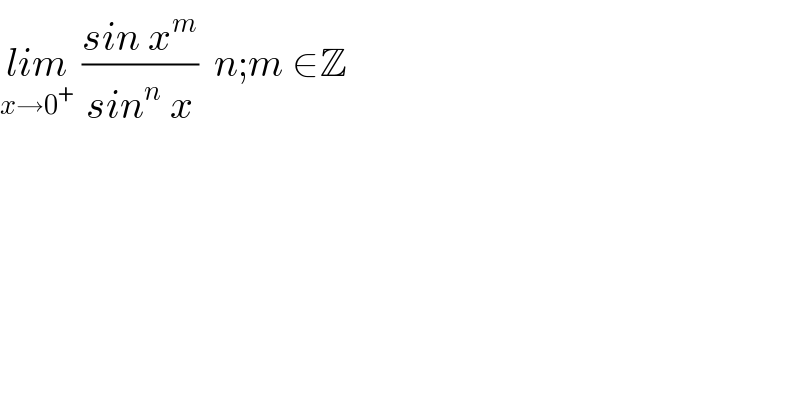
$$\underset{{x}\rightarrow\mathrm{0}^{+} } {{lim}}\:\frac{{sin}\:{x}^{{m}} }{{sin}^{{n}} \:{x}}\:\:{n};{m}\:\in\mathbb{Z} \\ $$
Answered by mrW1 last updated on 26/Jan/17
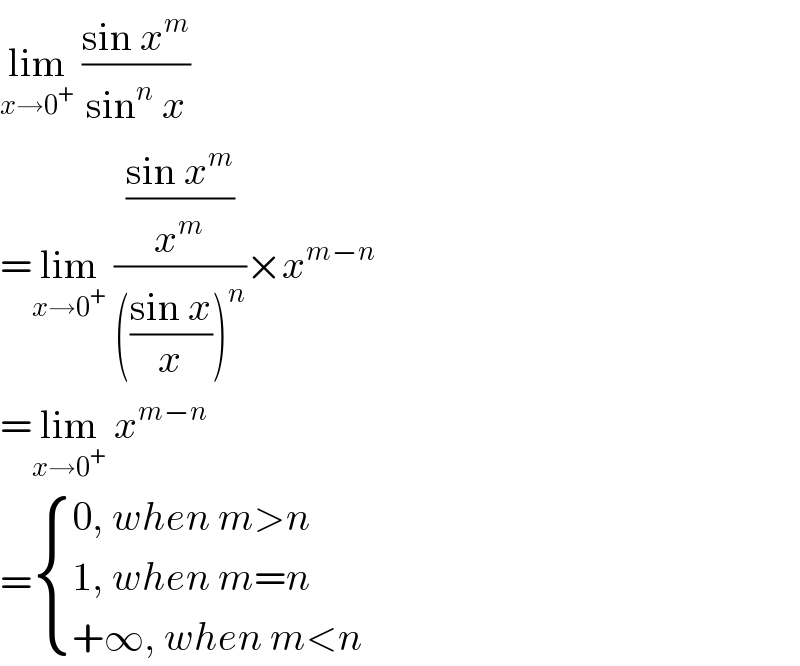
$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}^{{m}} }{\mathrm{sin}^{{n}} \:{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\frac{\mathrm{sin}\:{x}^{{m}} }{{x}^{{m}} }}{\left(\frac{\mathrm{sin}\:{x}}{{x}}\right)^{{n}} }×{x}^{{m}−{n}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:{x}^{{m}−{n}} \\ $$$$=\begin{cases}{\mathrm{0},\:{when}\:{m}>{n}}\\{\mathrm{1},\:{when}\:{m}={n}}\\{+\infty,\:{when}\:{m}<{n}}\end{cases} \\ $$
Commented by malwaan last updated on 27/Jan/17
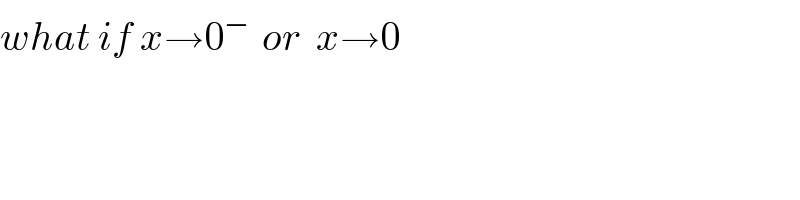
$${what}\:{if}\:{x}\rightarrow\mathrm{0}^{−\:} \:{or}\:\:{x}\rightarrow\mathrm{0} \\ $$
Commented by mrW1 last updated on 27/Jan/17
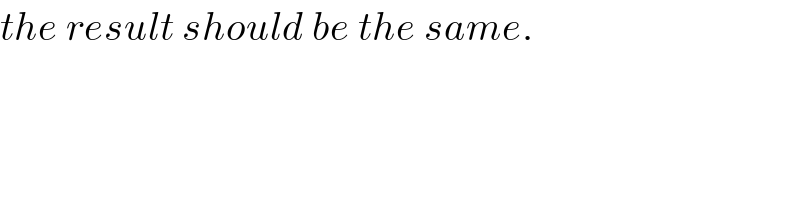
$${the}\:{result}\:{should}\:{be}\:{the}\:{same}. \\ $$
