Question Number 4773 by madscientist last updated on 08/Mar/16
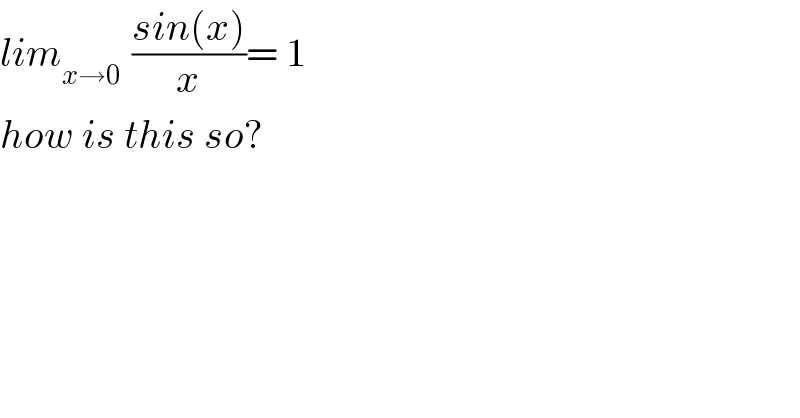
$${lim}_{{x}\rightarrow\mathrm{0}\:} \:\frac{{sin}\left({x}\right)}{{x}}=\:\mathrm{1} \\ $$$${how}\:{is}\:{this}\:{so}? \\ $$$$ \\ $$
Commented by Yozzii last updated on 13/Mar/16
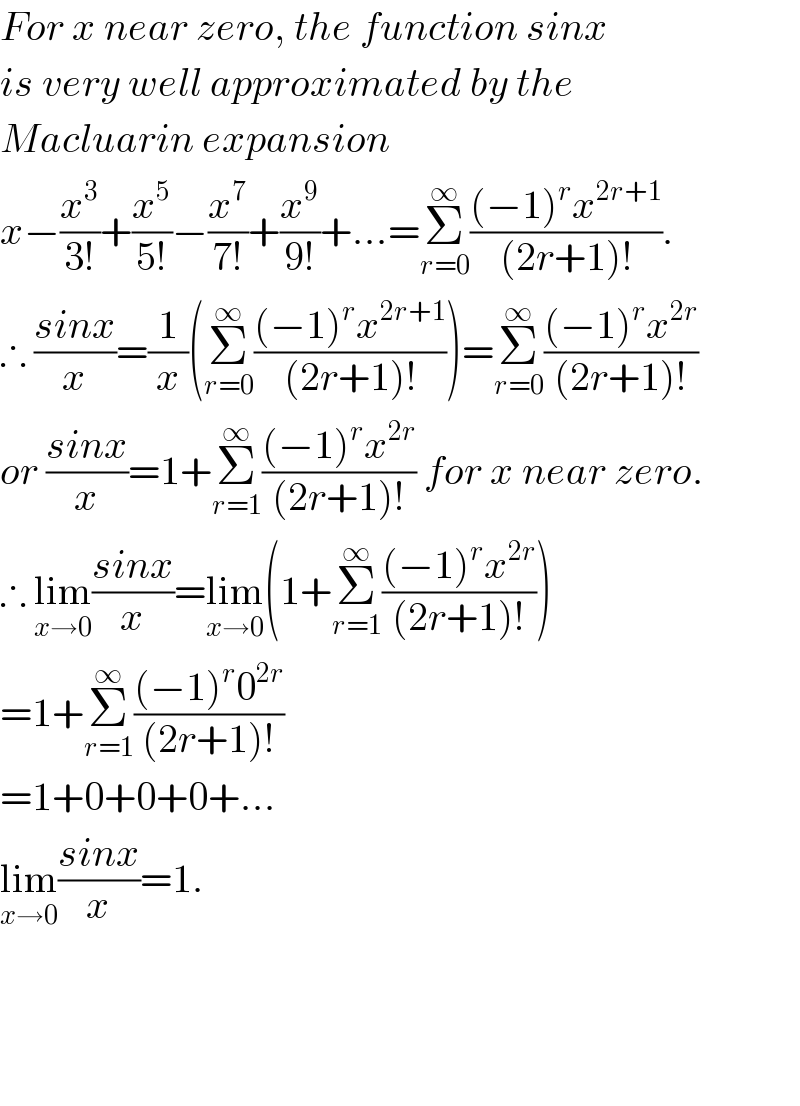
$${For}\:{x}\:{near}\:{zero},\:{the}\:{function}\:{sinx} \\ $$$${is}\:{very}\:{well}\:{approximated}\:{by}\:{the}\: \\ $$$${Macluarin}\:{expansion}\: \\ $$$${x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}−\frac{{x}^{\mathrm{7}} }{\mathrm{7}!}+\frac{{x}^{\mathrm{9}} }{\mathrm{9}!}+…=\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{r}} {x}^{\mathrm{2}{r}+\mathrm{1}} }{\left(\mathrm{2}{r}+\mathrm{1}\right)!}. \\ $$$$\therefore\:\frac{{sinx}}{{x}}=\frac{\mathrm{1}}{{x}}\left(\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{r}} {x}^{\mathrm{2}{r}+\mathrm{1}} }{\left(\mathrm{2}{r}+\mathrm{1}\right)!}\right)=\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{r}} {x}^{\mathrm{2}{r}} }{\left(\mathrm{2}{r}+\mathrm{1}\right)!} \\ $$$${or}\:\frac{{sinx}}{{x}}=\mathrm{1}+\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{r}} {x}^{\mathrm{2}{r}} }{\left(\mathrm{2}{r}+\mathrm{1}\right)!}\:{for}\:{x}\:{near}\:{zero}. \\ $$$$\therefore\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{sinx}}{{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{r}} {x}^{\mathrm{2}{r}} }{\left(\mathrm{2}{r}+\mathrm{1}\right)!}\right) \\ $$$$=\mathrm{1}+\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{r}} \mathrm{0}^{\mathrm{2}{r}} }{\left(\mathrm{2}{r}+\mathrm{1}\right)!} \\ $$$$=\mathrm{1}+\mathrm{0}+\mathrm{0}+\mathrm{0}+… \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{sinx}}{{x}}=\mathrm{1}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by malwaan last updated on 08/Mar/16
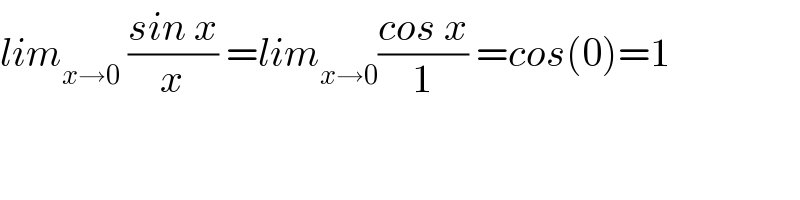
$${lim}_{{x}\rightarrow\mathrm{0}} \:\frac{{sin}\:{x}}{{x}}\:={lim}_{{x}\rightarrow\mathrm{0}} \frac{{cos}\:{x}}{\mathrm{1}}\:={cos}\left(\mathrm{0}\right)=\mathrm{1} \\ $$
Commented by Dnilka228 last updated on 10/Mar/16
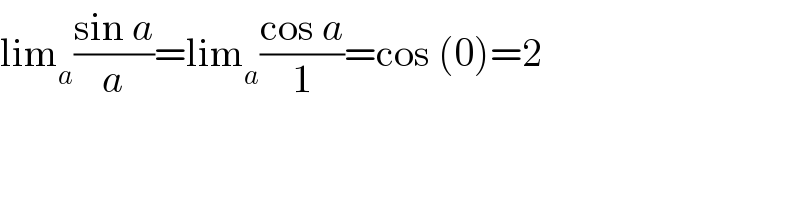
$$\mathrm{lim}_{{a}} \frac{\mathrm{sin}\:{a}}{{a}}=\mathrm{lim}_{{a}} \frac{\mathrm{cos}\:{a}}{\mathrm{1}}=\mathrm{cos}\:\left(\mathrm{0}\right)=\mathrm{2} \\ $$
